PROBLEM SOLVING INVOLVING HYPERBOLA
TLDRThe video presentation by Group 16, led by Adriana Girl Fernandez Mahaz, delves into solving problems involving hyperbolas, one of the four conic sections. They tackle two distinct problems, starting with a scenario involving radio signaling stations A and B and a plane flying west. Using the given speed of radio signals and the time difference in signal reception, they calculate the plane's location using hyperbolic geometry. The second problem involves two stations receiving a sound signal from a source, with a time difference that helps determine the equation of a hyperbola containing the source's location. The group effectively uses the properties of hyperbolas to solve these problems, showcasing the mathematical process and the final equations for each scenario.
Takeaways
- 📚 The presentation is focused on solving problems involving hyperbolas, one of the four conic sections.
- 📍 Problem one involves two radio signaling stations, A and B, and a plane flying west on a line 50 miles north of the line AB.
- 🕒 The radio signals travel at 0.2 miles per microsecond, and the plane receives the signal from B 400 microseconds before the one from A.
- 🔢 Given values include the distance between A and B (100 miles), the distance from the plane to the centers of A and B (50 miles each), and the time difference (400 microseconds).
- 📉 The plane's location is determined using the hyperbola equation and the values of a, b, and c derived from the problem's conditions.
- ✂️ The value of 'a' is calculated to be 40 miles by using the time difference and the speed of the signals.
- 📐 The formula c^2 = a^2 + b^2 is used to find the value of 'b', resulting in b^2 = 900 and b = 30 miles.
- 🧭 The hyperbola equation x^2/a^2 - y^2/b^2 = 1 is then used to find the plane's x-coordinate, which is calculated to be 77.77 miles.
- 📉 The second problem involves two stations receiving a sound signal from a source at point P with coordinates (x, y), with one station receiving the signal 4 seconds earlier than the other.
- 🎶 The speed of sound is given as 0.33 kilometers per second, and the time difference results in a distance of 1.32 kilometers.
- 📏 The value of 'a' for the hyperbola is determined to be 0.66 kilometers, and 'c' is known to be 1 kilometer from the problem's conditions.
- 📘 The value of 'b' is calculated using the relationship a^2 = b^2 + c^2, resulting in b = sqrt(1 - 0.66^2) or b = 0.75 kilometers.
- 📈 The final equation of the hyperbola containing point P is x^2/0.66^2 - y^2/0.75^2 = 1.
Q & A
What is the main topic of the video presentation?
-The main topic of the video presentation is solving problems involving hyperbolas, which are one of the four conic sections.
What is the first problem presented in the video about?
-The first problem is about determining the location of a plane flying west on a line 50 miles north of an east-west line connecting two radio signaling stations A and B, given the time difference in reception of signals from A and B.
What are the given distances in the first problem?
-The given distances are: 100 miles between stations A and B, and 50 miles north of the line AB for the plane's flight path.
What is the speed of the radio signals mentioned in the first problem?
-The speed of the radio signals is 0.2 miles per microsecond.
How much earlier does the signal from station B arrive at the plane compared to the signal from station A?
-The signal from station B arrives 400 microseconds earlier than the signal from station A.
What is the formula used to solve for the distance 'a' in the first problem?
-The formula used to solve for the distance 'a' is derived from the relationship pa - pb = 2a, where 'a' is the distance between the foci of the hyperbola and 'pa' and 'pb' are the distances from the plane to the respective foci.
What is the value of 'c' in the first problem?
-The value of 'c', which is the distance from the center of the hyperbola to each focus, is 50 miles.
How is the equation of the hyperbola derived in the first problem?
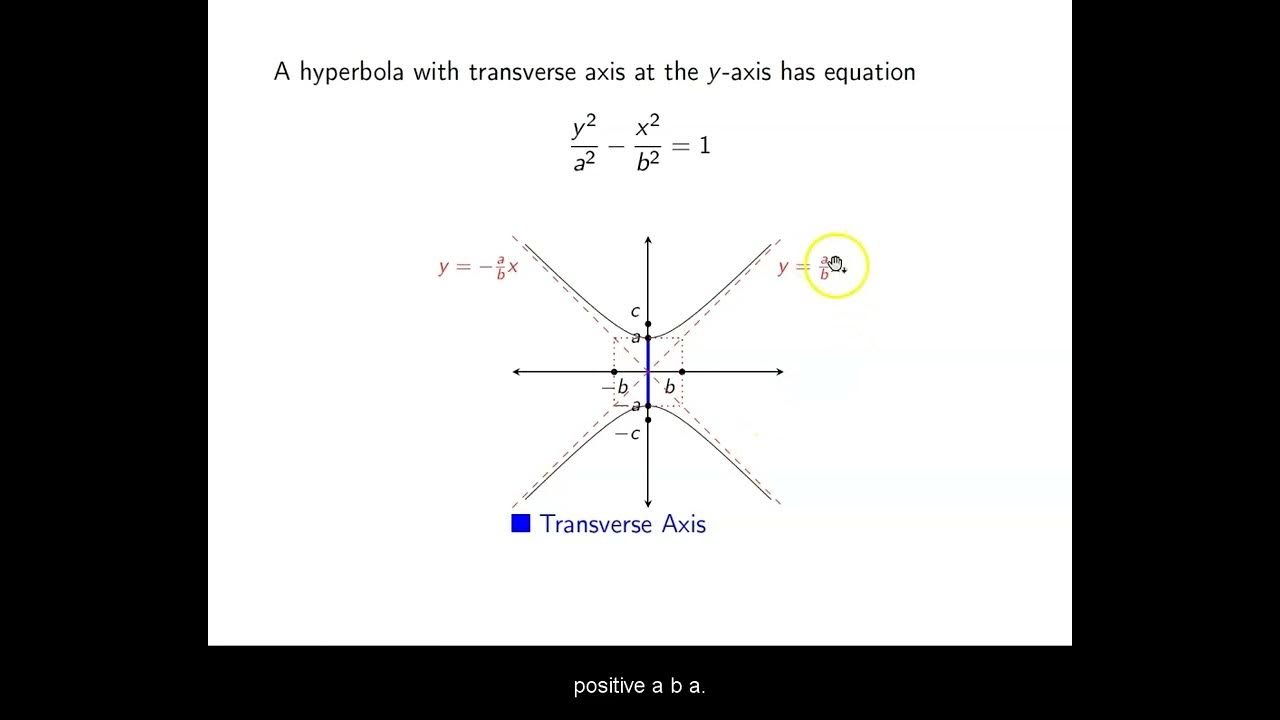
-The equation of the hyperbola is derived using the standard form \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \) and substituting the values of 'a', 'b', and 'c' to find the plane's location.
What is the final calculated location of the plane in the first problem?
-The final calculated location of the plane is at 77.77 miles west and 50 miles north of the line connecting the radio signaling stations A and B.
What is the second problem presented in the video about?
-The second problem is about finding the equation of a hyperbola containing a point P, given the time difference in reception of a sound signal by two stations located at (0, -1) and (0, 1), with a speed of sound of 0.33 kilometers per second.
What is the value of 'a' in the second problem, and how is it calculated?
-The value of 'a' in the second problem is 0.66 kilometers, calculated by dividing the distance the sound travels in 4 seconds (1.32 kilometers) by 2.
What is the equation of the hyperbola containing point P in the second problem?
-The equation of the hyperbola containing point P is \( \frac{x^2}{0.66^2} - \frac{y^2}{0.75^2} = 1 \).
Outlines
📚 Hyperbola Problem Solving Introduction
This paragraph introduces the video presentation by Group 16, led by Adriana Girl Fernandez Mahaz. The focus is on solving problems involving hyperbolas, one of the four conic sections. The first problem involves two radio signaling stations, A and B, located on an east-west line with a plane flying west on a line 50 miles north of the line. The problem requires finding the plane's location given the radio signals' travel times and speeds. Key information includes the distance between stations, the plane's position relative to the line, and the radio signals' speed and travel times. The solution process involves calculating the distance between the plane and the stations using the given data and applying the hyperbola equation to find the plane's exact location.
📐 Hyperbola Equation Derivation and Solution
The second paragraph delves into the mathematical derivation of the hyperbola equation to solve for a point P's coordinates, given the time difference in signal reception at two stations. The stations are 2 kilometers apart, and one receives a signal 4 seconds before the other, with the speed of sound provided as 0.33 kilometers per second. The solution involves determining the value of 'a' by dividing the distance the sound travels by 2a, which is found to be 0.66 kilometers. Using the relationship between a, b, and c in hyperbolas (a^2 = b^2 + c^2), the value of b is calculated to be 0.75. The paragraph concludes with the hyperbola's equation, x^2/0.66^2 - y^2/0.75^2 = 1, which represents the set of all points equidistant from the two foci. The speaker expresses gratitude to group members for their contributions to understanding and solving the problem.
Mindmap
Keywords
💡Hyperbola
💡Conic Sections
💡Radio Signaling Stations
💡Microsecond
💡Distance Calculation
💡Focus
💡Speed of Sound
💡Equation of Hyperbola
💡Transposition
💡Square Root
Highlights
Introduction to solving problems involving hyperbolas.
Problem 1 involves radio signaling stations A and B with a plane flying west.
The plane is 50 miles north of the line connecting stations A and B.
Radio signals are sent simultaneously from A and B at a speed of 0.2 miles per microsecond.
The signal from B arrives 400 microseconds before the one from A.
Calculation of the distance the signals traveled using the given rate and time.
Determination of the value of 'a' using the difference in signal arrival times.
Use of the hyperbola formula to find the value of 'b'.
Substitution of values into the hyperbola equation to find the location of the plane.
Final calculation of the plane's location at 77.77 miles west and 50 miles north.
Introduction to Problem 2 involving two stations receiving a sound signal from point P.
One station receives the signal 4 seconds earlier than the other, with a speed of sound at 0.33 km/s.
Inference that the focus of the hyperbola is at one of the stations based on the signal travel time.
Calculation of 'a' using the distance and time of the signal.
Determination of 'c' and subsequent calculation of 'b' using the relationship between a, b, and c.
Derivation of the equation of the hyperbola containing point P.
Presentation of the hyperbola's equation and its graphical representation.
Acknowledgment of group members for their contributions to solving the problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: