PROBLEM SOLVING INVOLVING ELLIPSE || PRECALCULUS
TLDRThis instructional video presents a detailed lesson on solving problems involving ellipses. The first problem involves calculating the height of a semi-elliptical bridge arc above water level at a point 30 feet horizontally from the center, given its dimensions. The second problem focuses on deriving the equation of a planet's elliptical orbit using the distances between vertices and foci. The video guides viewers through mathematical equations and calculations, ultimately providing the solutions and encouraging viewers to engage with the content through likes, subscriptions, and notifications for further educational content.
Takeaways
- 📚 The video lesson focuses on problem-solving involving ellipses.
- 🌉 Problem number one discusses a semi-elliptical arc of a bridge with a 22-foot height at its center and a 100-foot major axis.
- 📏 The task is to find the height of the arc 30 feet from the center horizontally, rounding to two decimal places.
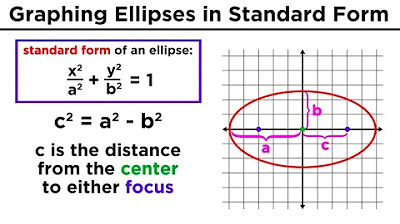
- 📐 The semi-ellipse's equation is derived from the general form of an ellipse: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \), with \( a = 50 \) and \( b = 22 \).
- 🔍 To solve for the height at a specific point, substitute the x-coordinate into the ellipse equation and solve for y.
- 🧮 The calculation involves substituting the x-coordinate (30 feet) into the ellipse equation and simplifying to find \( y^2 \).
- 📈 The value of \( y^2 \) is found to be 309.76, leading to \( y = \pm 17.6 \) feet, with the positive value indicating the height above water.
- 🚀 The second problem involves finding the equation of a planet's elliptical orbit with given distances between vertices and foci.
- ⭕ The vertices' distance is 1400 million kilometers, and the foci's distance is 800 million kilometers.
- 🔢 Using the relationship \( a^2 = b^2 + c^2 \) (where \( c \) is the distance between the foci), the orbit's equation is derived.
- 🌌 The final equation of the orbit is \( \frac{x^2}{700^2} + \frac{y^2}{574.46^2} = 1 \).
- 👋 The video concludes with an invitation to like, subscribe, and hit the bell button for more educational content.
Q & A
What is the main topic discussed in the video lesson?
-The main topic discussed in the video lesson is problem-solving involving ellipses.
What shape is the arc of the bridge in the first problem?
-The arc of the bridge is in the shape of a semi-ellipse.
What are the dimensions of the semi-ellipse arc of the bridge in the first problem?
-The semi-ellipse arc is 22 feet high in the middle and 100 feet across its major axis.
How high above the water level is the arc at a point 30 feet from the center horizontally, according to the first problem?
-The arc is 17.6 feet above the water level at a point 30 feet from the center horizontally.
What is the equation of an ellipse in terms of its major and minor axes?
-The equation of an ellipse is \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \), where \( a \) is the semi-major axis and \( b \) is the semi-minor axis.
What is the relationship between the semi-major axis, semi-minor axis, and the distance between the foci in an ellipse?
-The relationship is given by the equation \( a^2 = c^2 + b^2 \), where \( c \) is the distance from the center to each focus.
What is the distance between the vertices of the elliptical orbit in the second problem?
-The distance between the vertices of the elliptical orbit is 1400 million kilometers.
What is the distance between the foci of the elliptical orbit in the second problem?
-The distance between the foci of the elliptical orbit is 800 million kilometers.
What is the equation of the orbit in the second problem?
-The equation of the orbit is \( \frac{x^2}{700^2} + \frac{y^2}{574.46^2} = 1 \).
What is the value of \( b^2 \) in the equation of the orbit in the second problem?
-The value of \( b^2 \) is 574.46 squared, which is derived from \( b^2 = 700^2 - 400^2 \).
What is the purpose of the video lesson?
-The purpose of the video lesson is to teach viewers how to solve problems involving ellipses and to provide step-by-step solutions to the given problems.
Outlines
🌉 Calculating the Height of a Semi-Elliptical Bridge Arc
This paragraph discusses a mathematical problem involving the calculation of the height of a semi-elliptical arc of a bridge above the water level at a specific horizontal distance from the center. The arc is described with a major axis of 100 feet and a height of 22 feet at the center. The problem requires finding the height of the arc 30 feet from the center. The solution involves setting up the equation of the ellipse \( \frac{x^2}{50^2} + \frac{y^2}{22^2} = 1 \) and substituting the x-coordinate to solve for y, which represents the height. The calculation leads to a height of approximately 17.6 feet above the water level at the specified point.
🚀 Equation of a Planet's Elliptical Orbit
The second paragraph presents a problem related to celestial mechanics, specifically the calculation of the equation of an elliptical orbit of a planet. Given the distance between the vertices (1400 million kilometers) and the distance between the foci (800 million kilometers), the task is to derive the orbit's equation. The solution uses the relationship between the semi-major axis (a), semi-minor axis (b), and the distance between the foci (c), which is \( c^2 = a^2 - b^2 \). By substituting the given values, the semi-minor axis b is calculated to be approximately 574.46 million kilometers. Consequently, the orbit's equation is given by \( \frac{x^2}{700^2} + \frac{y^2}{574.46^2} = 1 \).
📚 Conclusion and Invitation to Further Learning
The final paragraph serves as a conclusion to the video lesson, summarizing the content covered and encouraging viewers to continue learning. The speaker thanks the audience for watching, expresses hope that they have gained knowledge, and prompts them to like, subscribe, and hit the bell button for updates on more video tutorials. The channel is presented as a guide for learning and education.
Mindmap
Keywords
💡Ellipse
💡Major Axis
💡Semi-Ellipse
💡Vertices
💡Foci
💡Height
💡Equation of Ellipse
💡Square Root
💡Pythagorean Theorem
💡Scientific Calculator
Highlights
Introduction to problem-solving involving ellipses.
Problem 1 involves a semi-elliptical bridge arc with a major axis at water level.
The bridge arc is 22 feet high in the middle and 100 feet across its major axis.
The task is to find the height of the arc 30 feet from the center horizontally.
The semi-ellipse is visualized with its geometric properties.
The major axis length is given as 100 feet, and the vertex height as 22 feet.
The equation of the ellipse is derived using the standard form.
The x-coordinate is substituted with 30 feet to find the corresponding y-coordinate.
An algebraic manipulation is performed to solve for the y-coordinate.
The height of the arc above water level is calculated to be 17.6 feet.
Problem 2 discusses the orbit of a planet in the shape of an ellipse.
The distance between the vertices and foci of the elliptical orbit is given.
The vertices' distance is 1400 million kilometers, and the foci's distance is 800 million kilometers.
The standard form of an ellipse equation is used to derive the orbit's equation.
The relationship between the vertices, foci, and center is utilized to find 'a' and 'b'.
The Pythagorean theorem is applied to find the values of 'a' and 'b'.
The final equation of the orbit is provided with 'a' and 'b' values.
The video concludes with a summary of the problem-solving process and an invitation to subscribe for more tutorials.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: