Writing Definite Integrals from Limits of Riemann Sums

turksvids

13 Jan 201809:09

EducationalLearning

32 Likes 10 Comments

TLDRThe video script focuses on the transition of Riemann sums into definite integrals, specifically within the context of AP Calculus. It explains the concept by first illustrating the process of dividing the interval [a, b] into n equal slices with width Δx, and then constructing right-endpoint rectangles. The script emphasizes the importance of identifying the evaluation points (x_i = a + iΔx) and using them to determine the bounds a and b. Several examples are provided to demonstrate the process, including calculating the integral of functions like √x and sin(x), and interpreting a given graph to find the corresponding integral. The key takeaway is the methodical approach to understanding the relationship between Δx, the evaluation points, and the function f(x), which is crucial for converting Riemann sums into definite integrals.

Takeaways

📐 **Understanding Riemann Sums**: The video focuses on converting Riemann sums into definite integrals, emphasizing the method used in AP Calculus.
📈 **Right Riemann Sums**: It's mentioned that in AP Calculus, students typically deal with right Riemann sums, which use the right endpoint of each interval.
🔢 **Calculating Δx**: The process involves calculating the change in x (Δx), which is the width of each subinterval in the partition of the function's domain.
📉 **Evaluating at Endpoints**: The height of each rectangle in the Riemann sum is determined by evaluating the function at the right endpoint of each subinterval.
🔑 **Finding a and b**: By using the evaluation points, one can deduce the bounds 'a' and 'b' of the definite integral.
🏗️ **Constructing the Integral**: The definite integral is constructed by multiplying the base (Δx) by the sum of the function evaluated at each endpoint.
🚀 **Limit as n Approaches Infinity**: The definite integral is represented as the limit of the Riemann sum as the number of rectangles (n) approaches infinity.
✅ **Multiple Approaches**: The video shows that there are multiple ways to interpret the function and bounds, leading to equivalent integrals.
📚 **Substitution**: The concept of substitution is highlighted, where changing the function can lead to different evaluation points but the same integral value.
📊 **Graph Interpretation**: An example is given where the definite integral is interpreted from a graph, emphasizing the need to identify the function and bounds from the visual information.
🔍 **Key Concept**: The importance of understanding the relationship between Δx, the evaluation points, and the function to calculate the definite integral is stressed.

Q & A

What is the main topic of the video?
-The video discusses the conversion of Riemann sums into definite integrals, focusing on the right Riemann sums which are commonly encountered in AP Calculus.
What is the significance of ΔX in the context of Riemann sums?
-ΔX represents the width of each subinterval in the partition of the interval [a, b], and it is used to create the rectangles in the Riemann sum approximation of the definite integral.
How is the right endpoint of each rectangle determined in a right Riemann sum?
-The right endpoint of each rectangle is determined by adding the width of the rectangle (ΔX) multiplied by the index of the rectangle (i) to the starting point 'a'.
What is the formula for the evaluation point X_i in terms of ΔX and i?
-The evaluation point X_i is calculated as a + i * ΔX, where 'a' is the starting point of the interval, 'i' is the index of the rectangle, and ΔX is the width of each subinterval.
How can you determine the bounds 'a' and 'b' of the definite integral using the evaluation point X_i?
-By plugging in i = 0 into the formula for X_i, you get 'a', and by plugging in i = n (the number of rectangles), you get 'b', since X_n = a + n * ΔX = b.
What is the area of each rectangle in the Riemann sum?
-The area of each rectangle is the product of its base (ΔX) and height (f(X_i)), which is the function value at the evaluation point.
How is the definite integral expressed in terms of the Riemann sum?
-The definite integral is expressed as the limit as n approaches infinity of the Riemann sum, which is the sum of the areas of all the rectangles, ΔX * (f(a + ΔX) + f(a + 2ΔX) + ... + f(a + nΔX)).
What is the first step when solving a problem involving Riemann sums in the video?
-The first step is to identify ΔX, which is usually given at the beginning or end of the problem statement.
How can you find the function f(x) when given a Riemann sum problem?
-You can find the function f(x) by looking at what is being plugged into the function, which will give you clues about the form of f(x).
What are the two different ways the video presents to write the integral of √(x) from 1 to 2?
-The two ways are: 1) considering the integral from 1 to 2 of √(x) dx with X_i as 1 + i * (1/N), and 2) considering the integral from 0 to 1 of √(1 + x) dx with X_i as i * (1/N).
How does the video approach a problem where the definite integral is not given but the function and interval are?
-The video suggests determining the function f(x), identifying the interval endpoints 'a' and 'b', and then writing the limit of the Riemann sum to find the definite integral over that interval.

Outlines

00:00

📐 Understanding Riemann Sums and Definite Integrals

This paragraph introduces the topic of converting Riemann sums into definite integrals and focuses on the right Riemann sums commonly encountered in AP Calculus. It explains the process of calculating the definite integral by dividing the interval [a, b] into n equal slices, using the right endpoint of each slice as the evaluation point, and finding the height of each rectangle by plugging the evaluation point into the function. The area of each rectangle is found by multiplying the base (Δx) by the height (f(xi)). The definite integral is then expressed as the limit of the sum of these rectangle areas as n approaches infinity.

05:02

🔢 Examples of Converting Riemann Sums to Definite Integrals

This paragraph presents three examples to illustrate the process of converting Riemann sums to definite integrals. The first example involves finding the definite integral of the function f(x) = √(x) over the interval [1, 2]. The second example shows an alternative way to write the same integral by choosing a different function f(x) = √(1+x). The third example involves finding the definite integral of f(x) = ∛(x) over the interval [-1, 3] given a graph of the function. In each case, the key steps are identifying the function f(x), determining the interval endpoints a and b, and expressing the definite integral as the limit of the Riemann sum using the evaluation points xi = a + iΔx.

Mindmap

Keywords

💡Riemann sums

Riemann sums are a method used to approximate the area under a curve, which is the integral of a function. In the context of the video, they are used to transition into the concept of definite integrals by breaking down the process of calculating the area under a curve using rectangles of varying heights and widths.

💡Definite integrals

Definite integrals represent the exact area under a curve between two points, denoted as 'a' and 'b'. The video focuses on how to convert Riemann sums into definite integrals, which is a fundamental concept in calculus for finding areas and volumes.

💡AP Calculus

AP Calculus is a high school advanced placement course that covers calculus topics. The video is tailored to this audience, emphasizing the teaching and understanding of Riemann sums and definite integrals as commonly encountered in this course.

💡Right Riemann sums

Right Riemann sums are a specific type of Riemann sum where the height of each rectangle used to approximate the area under the curve is determined by the function's value at the right endpoint of each subinterval. The video discusses this method in detail as it is commonly used in AP Calculus.

💡Evaluation points

Evaluation points are the specific points within each subinterval where the function's value is calculated to determine the height of the rectangles in a Riemann sum. The video explains how to find these points using the formula X_sub_I = a + I * Delta X.

💡Delta X

Delta X, often denoted as (b - a) / n, represents the width of each subinterval in the Riemann sum approximation. It is a key component in calculating the evaluation points and the area of each rectangle in the sum.

💡Limits

In calculus, limits are a fundamental concept used to understand the behavior of functions as inputs approach a certain value. The video discusses how the concept of limits is applied to Riemann sums to transition to definite integrals as the number of rectangles, n, approaches infinity.

💡Integral

An integral is a mathematical concept that represents the area under a curve between two points. The video script discusses how to express integrals using the limit of Riemann sums, which is a core topic in calculus.

💡Function

A function, often denoted as f(x), is a mathematical relationship between two variables. The video script involves functions such as f(x) = √x and f(x) = sin(x), which are integrated over specific intervals to find areas under their respective curves.

💡Substitution

Substitution is a technique used in calculus to change variables in an integral to simplify the problem. The video mentions that if substitution is used on the bottom integral, it turns into the top one, indicating the equivalence of different integral expressions.

💡Graphical representation

The video includes an example where the integral is not given explicitly but is represented graphically. The task is to interpret the graph to determine the function, the interval, and then calculate the definite integral, which is a practical skill in understanding and applying calculus concepts.

Highlights

The video discusses the conversion of Riemann sums into definite integrals, focusing on the relationship between the two mathematical concepts.

The focus is on AP calculus, particularly relevant for students and educators involved in that curriculum.

Explains the concept of ΔX, which is the width of each slice when dividing the interval [a, b] into n equal parts.

Demonstrates how to create right Riemann sums by using the right endpoint of each interval slice.

Introduces the formula for calculating the evaluation point X_sub_I, which is crucial for determining the function's value at each interval.

Shows how to find the definite integral by summing the areas of the rectangles formed by the Riemann sum.

Illustrates the process of taking the limit as n approaches infinity to transition from a Riemann sum to a definite integral.

Presents an example involving the function f(x) = √x, demonstrating how to identify the correct function and interval bounds.

Discusses the importance of understanding the relationship between the evaluation points and the interval bounds a and b.

Provides an alternative approach to the previous example by choosing a different function f(x) = √(1 + x) and showing the resulting changes.

Highlights that different interpretations of the function and interval can lead to equivalent integrals with the same numerical value.

Introduces a second example with the function f(x) = sin(x) and explains how to determine the interval [0, π] for integration.

Demonstrates how to adjust the evaluation point formula X_sub_I when a different function is chosen, affecting the calculation of a and b.

Explains that understanding the function and interval is key to successfully calculating the definite integral from a Riemann sum.

Presents a unique scenario where the definite integral is derived from a given graph, rather than explicit function and interval.

Shows how to calculate the definite integral of the cube root function over the interval [-1, 3] using the limit of a Riemann sum.

Emphasizes the importance of knowing the function, interval bounds, and the relationship between ΔX and evaluation points for successful integration.

The video concludes by reinforcing the practical steps involved in converting Riemann sums to definite integrals and encourages viewers in their mathematical understanding.

Transcripts

Browse More Related Video

Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus

The Definite Integral Part II: Using Summation Notation to Define the Definite Integral

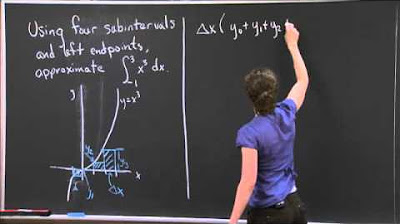
Riemann sum | MIT 18.01SC Single Variable Calculus, Fall 2010

The Definite Integral Part III: Evaluating From The Definition

Switching bounds of definite integral | AP Calculus AB | Khan Academy

Fundamental theorem of calculus (Part 2) | AP Calculus AB | Khan Academy

Writing Definite Integrals from Limits of Riemann Sums

Takeaways

Q & A

What is the main topic of the video?

What is the significance of ΔX in the context of Riemann sums?

How is the right endpoint of each rectangle determined in a right Riemann sum?

What is the formula for the evaluation point X_i in terms of ΔX and i?

How can you determine the bounds 'a' and 'b' of the definite integral using the evaluation point X_i?

What is the area of each rectangle in the Riemann sum?

How is the definite integral expressed in terms of the Riemann sum?

What is the first step when solving a problem involving Riemann sums in the video?

How can you find the function f(x) when given a Riemann sum problem?

What are the two different ways the video presents to write the integral of √(x) from 1 to 2?

How does the video approach a problem where the definite integral is not given but the function and interval are?