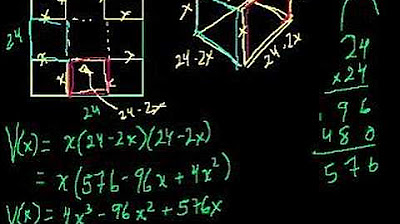Calculus Optimization: Apple Orchard Problem

turksvids
23 Dec 201904:42
EducationalLearning
32 Likes 10 Comments

TLDRThis video tackles an optimization problem concerning an apple orchard. With an initial 50 trees producing 800 apples each, the output per tree decreases by 10 apples for every additional tree planted. The presenter guides viewers through setting up a table to track the output and then employs algebra to formulate the problem mathematically. By calculating the total output as a function of the number of trees added (X), they derive a function to maximize. Using calculus, they find the critical point where the derivative of the output function is zero, which indicates a maximum. The second derivative test confirms this maximum, leading to the conclusion that adding 15 trees to the orchard will optimize its output. The video is an engaging lesson in applying mathematical concepts to real-world problems.

Takeaways
  • 🍎 The problem is about optimizing the output of an apple orchard by adding more trees.
  • 🌳 Initially, there are 50 apple trees, each producing 800 apples.
  • 🔽 For each additional tree planted, the output per tree decreases by 10 apples.
  • 📈 The goal is to determine the optimal number of trees to add to maximize the orchard's total output.
  • 📊 The problem is set up by creating a table to track the number of trees, output per tree, and total output.
  • 🌱 An algebraic equation is formulated with 'X' representing the number of additional trees to be planted.
  • 🧮 The total output 'a' is calculated as the product of (50 + X) and (800 - 10X) apples.
  • 📌 To find the maximum output, the derivative of the output function is taken and set to zero to find critical points.
  • 📶 The second derivative test is used to confirm that the critical point found is indeed a maximum.
  • 🔢 After calculations, it is determined that adding 15 trees to the orchard will maximize the output.
  • 📝 The final recommendation is to add 15 more trees to the orchard for optimal production.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is solving an optimization problem related to an apple orchard to determine the optimal number of additional trees to be planted for maximizing the orchard's output.

  • How many apple trees are currently in the orchard?

    -There are currently 50 apple trees in the orchard.

  • What is the initial output of apples per tree?

    -The initial output of apples per tree is 800.

  • How does the output per tree change with each additional tree planted?

    -For each additional tree planted in the orchard, the output per tree drops by 10 apples.

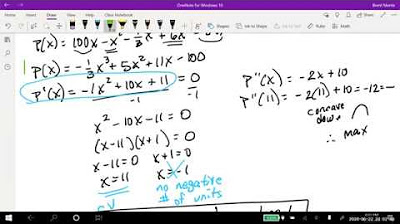
  • What is the formula used to calculate the total output of the orchard?

    -The total output of the orchard is calculated by the product of the number of trees and the output per tree, which is given by the formula (50 + X) * (800 - 10X), where X is the number of additional trees planted.

  • What mathematical method is used to find the maximum output?

    -The method used to find the maximum output is calculus, specifically by taking the derivative of the output function and setting it to zero to find critical points, and then using the second derivative test to confirm that it is a maximum.

  • What does the derivative of the output function represent?

    -The derivative of the output function represents the rate of change of the total output with respect to the number of additional trees planted.

  • How many additional trees should be planted to maximize the orchard's output according to the video?

    -According to the video, 15 additional trees should be planted to maximize the orchard's output.

  • What is the second derivative of the output function?

    -The second derivative of the output function is -20, which indicates that the function is concave down, confirming the presence of a maximum.

  • Why is it beneficial to draw a picture when solving optimization problems?

    -Drawing a picture is beneficial because it helps visualize the function and its behavior, making it easier to understand the concept of maxima and minima, and to interpret the results of the mathematical analysis.

  • What is the final recommendation for the orchard to optimize its output?

    -The final recommendation is to add 15 trees to the existing orchard to optimize its output.

  • How does the video relate the apple orchard optimization problem to other real-world scenarios?

    -The video relates the apple orchard optimization problem to scenarios such as building apartments in a building or managing a peach orchard, indicating that the problem-solving approach can be applied to various contexts involving resource allocation and optimization.

Outlines
00:00
🍎 Optimization Problem Introduction

The video begins with an introduction to an optimization problem involving an apple orchard. The goal is to determine the optimal number of additional trees to plant in order to maximize the orchard's output. The current orchard has 50 trees, each capable of producing 800 apples. However, for every additional tree planted, the output per tree decreases by 10 apples. The presenter suggests setting up a table to track the trees, output per tree, and total output, starting with the initial 50 trees and 40,000 apples, and then incrementally adding trees to observe the effect on total output.

Mindmap
Keywords
💡Optimization problem
An optimization problem involves finding the best solution within a set of possible solutions, often with constraints. In the video, the main theme revolves around optimizing the output of an apple orchard by determining the ideal number of additional trees to plant. The problem is framed in terms of maximizing the total apple production given the constraints of reduced output per tree as more trees are added.
💡Apple orchard
An apple orchard is a type of agricultural land where apple trees are cultivated for the production of apples. In the context of the video, the apple orchard serves as the setting for the optimization problem. The orchard initially has 50 apple trees, and the goal is to find out how many more trees should be added to maximize the orchard's output.
💡Output per tree
Output per tree refers to the number of apples each individual tree can produce. In the video, it is stated that each tree can produce 800 apples, but this number decreases by 10 for each additional tree planted. This concept is central to the optimization problem as it directly affects the total production of the orchard.
💡Algebra
Algebra is a branch of mathematics that uses symbols and rules to represent numbers and operations. In the video, algebra is used to formulate the optimization problem mathematically. The presenter sets up an algebraic expression to represent the total output of the orchard as a function of the number of trees and then uses algebraic techniques to find the maximum value of this function.
💡Derivative
In calculus, a derivative represents the rate at which a function is changing at a given point. In the video, the presenter uses the concept of the derivative to find the critical points of the function representing the orchard's output. By setting the derivative equal to zero, the presenter identifies points where the output could potentially reach a maximum or minimum.
💡Critical points
Critical points are points on a function where the derivative is zero or undefined, often indicating potential maxima or minima. In the context of the video, the presenter finds the critical points by setting the derivative of the output function to zero, which helps in identifying the number of trees that would maximize the orchard's output.
💡Second derivative test
The second derivative test is a method used in calculus to determine whether a critical point is a maximum, minimum, or inflection point by analyzing the sign of the second derivative of a function. In the video, the presenter uses the second derivative test to confirm that the critical point found indeed represents a maximum output for the orchard.
💡Concave down
A function is said to be concave down if its graph curves in a shape that resembles an inverted 'U'. In the video, the presenter concludes that the output function is concave down based on the negative value of the second derivative, which indicates that the function has a maximum at the critical point found.
💡Total output
Total output refers to the sum of all individual outputs, in this case, the total number of apples produced by all the trees in the orchard. The video's optimization problem aims to maximize the total output by determining the optimal number of trees to plant, taking into account the decrease in output per tree as more trees are added.
💡Product rule
The product rule is a fundamental theorem in calculus for differentiating products of two functions. In the video, the presenter applies the product rule to find the derivative of the total output function, which is a product of the number of trees and the output per tree.
💡Maximum
A maximum is the highest value that a function can attain. In the context of the video, the goal is to find the number of additional trees that, when planted, will result in the maximum total output of apples from the orchard. The concept of a maximum is central to the optimization problem being solved.
Highlights

The video discusses an optimization problem related to an apple orchard to maximize its output.

There are initially 50 apple trees in the orchard, each producing 800 apples.

For each additional tree planted, the output per tree decreases by 10 apples.

The goal is to determine the optimal number of trees to add to the orchard to maximize its total output.

The problem can be solved by setting up a table to track the output for each number of trees.

Starting with 50 trees, the total output is 40,000 apples.

Planting an additional tree increases the total output, so it makes sense to plant more trees.

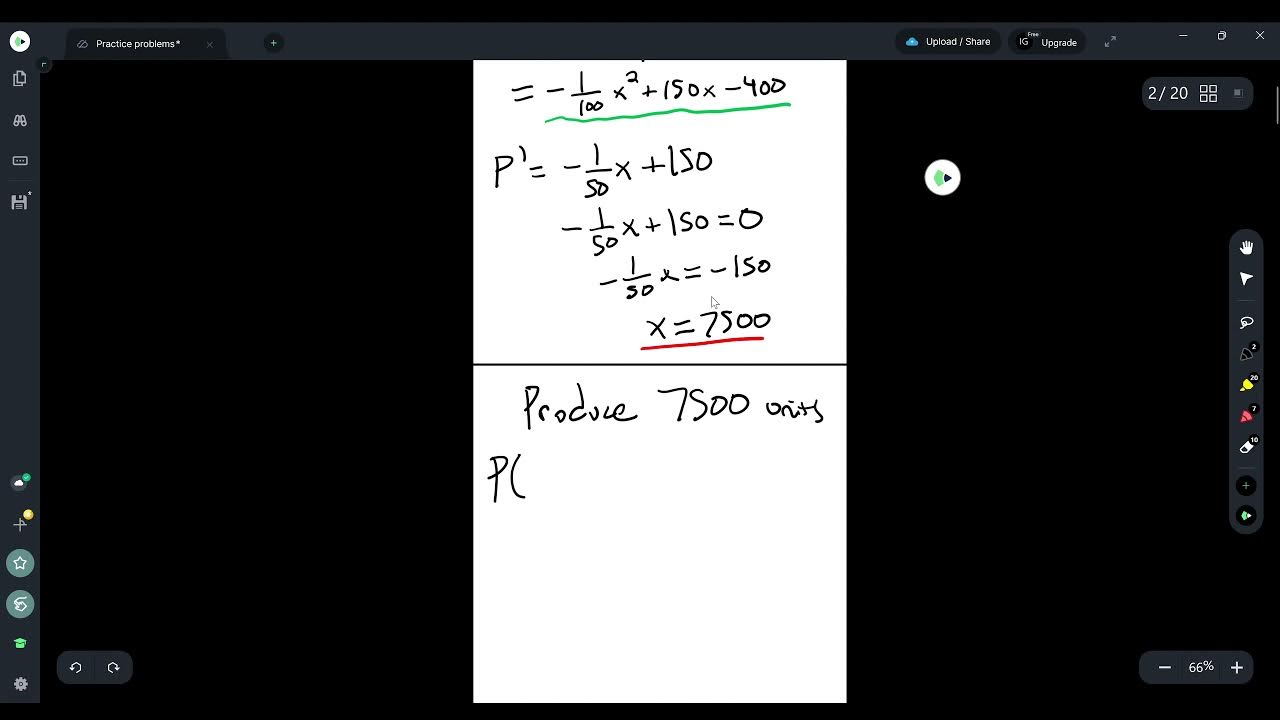
The algebraic expression for total output is derived as (50 + X) * (800 - 10X), where X is the number of additional trees.

To maximize the output, take the derivative of the expression and set it equal to zero to find critical points.

The first derivative a' is -20X + 300, which is set to zero to find the optimal number of trees.

Solving for X gives the optimal number of additional trees as 15.

To confirm it's a maximum, the second derivative test is used. The second derivative is -20, indicating a maximum.

The conclusion is that 15 more trees should be added to the orchard to optimize its output.

The video provides a step-by-step approach to solving the optimization problem using algebraic methods.

The problem is a common one in optimization, with applications beyond just orchards, such as in apartment buildings.

The video uses a table and algebraic expressions to model and solve the problem.

The process involves finding the critical points by setting the first derivative equal to zero.

The second derivative test confirms the critical point corresponds to a maximum output.

The video concludes with a clear answer and explanation of how to optimize the orchard's output by adding 15 trees.

Transcripts

Browse More Related Video

Maximization Word Problem #1!

BusCalc 17 Critical Points

Math 11 - Section 3.5

Managerial Economics 1.2: Univariate Optimization

Optimization with Calculus 2

Optimization Problem Examples

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Optimization ProblemApple OrchardMathematical SolutionProduction MaximizationTree PlantingOutput AnalysisDerivative TestSecond DerivativeConcave Down CurveCritical PointsMaximization Strategy