2022 AP Calculus AB & AP Calculus BC Exam FRQ #4
TLDRIn this educational video, the presenter tackles a problem from the 2022 AP Calculus exams involving an ice sculpture that melts in a conical shape. The problem requires using a table of values to approximate the rate of change of the radius over time, apply the Intermediate Value Theorem to find a specific time when the rate of change of the radius equals a given value, and calculate the rate of change of the cone's volume with respect to time. The presenter emphasizes the importance of not simplifying numerical values unnecessarily, as it can lead to errors and loss of points. The video provides a step-by-step approach to solving the problem, including using the average rate of change, applying the Intermediate Value Theorem, and employing a right Riemann sum for approximation. The presenter also discusses the importance of showing all work and understanding the underlying mathematical concepts, such as differentiability and continuity, which are crucial for solving calculus problems effectively.
Takeaways
- 📚 The video discusses a problem from the 2022 AP Calculus exams, focusing on a table problem involving an ice sculpture that melts in a conical shape.
- ⛄ The radius of the ice sculpture's base is modeled by a twice differentiable function r(t), where r'(t) represents the rate of change of the radius over time in days.
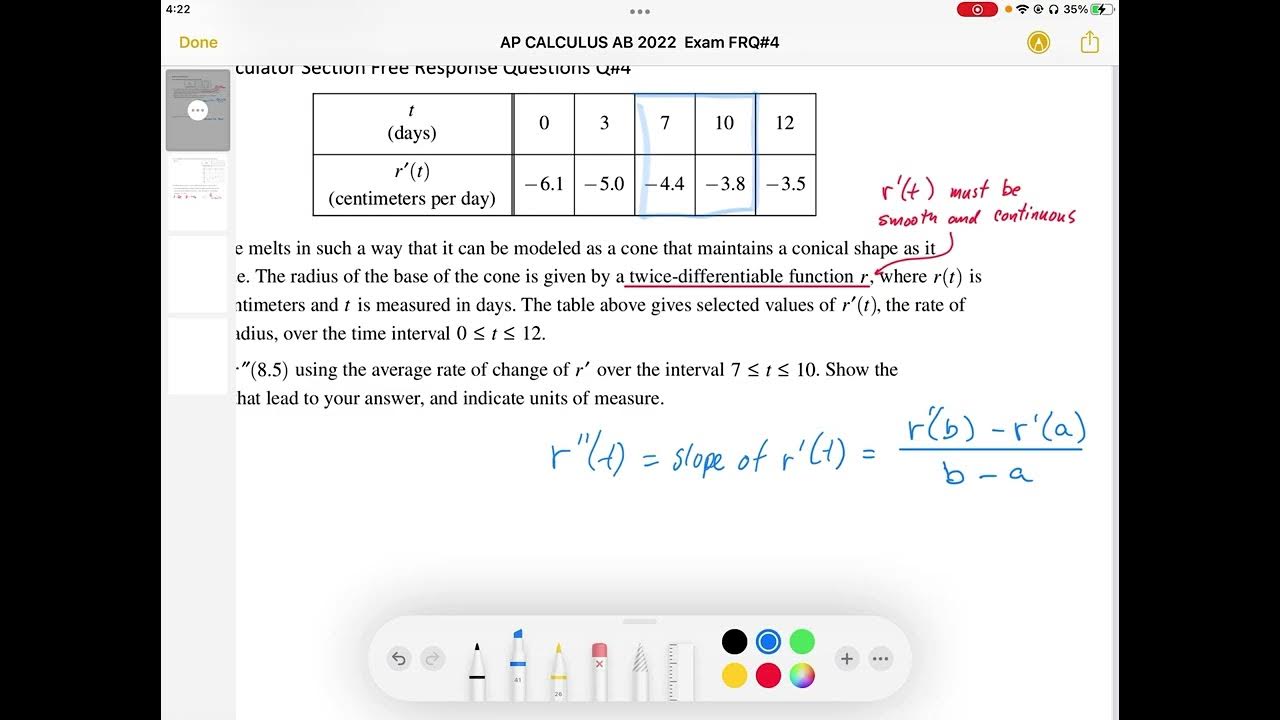
- 📊 Part A of the problem involves approximating the second derivative of r at t=8.5 using the average rate of change of r' over the interval from 7 to 10.
- 🧮 The average rate of change is calculated as (r'(10) - r'(7)) / (10 - 7), and the units are centimeters per day per day (cm/day/day).
- ❓ Part B asks if there's a time t between 0 and 3 when r'(t) equals -6, which is answered using the Intermediate Value Theorem (IVT), given r' is continuous as r is twice differentiable.
- 🔢 The video emphasizes the importance of not simplifying numerical values unnecessarily, to avoid errors and loss of points.
- 📈 For the next part, a right Riemann sum with four subintervals is used to approximate the integral of r'(t) from 0 to 12, without simplifying the expression.
- 📐 The height of the cone decreases at a constant rate of 2 cm/day, and at t=3 days, the radius is 100 cm and the height is 50 cm.
- 🔄 The rate of change of the volume of the cone with respect to time (dv/dt) is found using implicit differentiation and the given formula for the volume of a cone.
- 📋 Values for r, h, r'(t), and h'(t) are identified from the problem statement and table to calculate dv/dt.
- ⏱️ The final answer for dv/dt includes the units cubic centimeters per day (cm³/day), and the video advises against simplifying further to avoid potential errors.
- 👍 The video concludes with a reminder that the process demonstrated is helpful for understanding the problem-solving approach for similar AP Calculus exam questions.
Q & A
What type of problem is discussed in the video?
-The video discusses a table problem from the 2022 AP Calculus exams, specifically number four, which involves an ice sculpture modeled as a cone that maintains its shape as it melts.
How is the radius of the base of the cone related to time in the problem?
-The radius of the base of the cone, denoted as r(t), is given by a twice differentiable function where r is measured in centimeters and t is measured in days.
What does part a of the problem ask for?
-Part a asks to approximate r''(8.5), the second derivative of the radius with respect to time at t=8.5 days, using the average rate of change of r' over the interval from t=7 to t=10.
How is the average rate of change calculated in part a?
-The average rate of change is calculated as (r'(10) - r'(7)) / (10 - 7), where r'(10) is the rate of change of the radius at t=10 days and r'(7) is the rate of change at t=7 days.
What values are used to calculate the average rate of change in part a?
-The values used are r'(10) = -3.8 cm/day and r'(7) = -4.4 cm/day, which are taken from the table provided in the problem.
What is the unit of measure for r''(8.5)?
-The unit of measure for r''(8.5) is centimeters per day per day, or alternatively, it can be written as centimeters per day squared.
What theorem is used to determine if there is a time t between 0 and 3 for which r'(t) equals -6?
-The Intermediate Value Theorem (IVT) is used to determine if there is such a time t, given that r' is continuous.
Why is the Intermediate Value Theorem applicable in this problem?
-The IVT is applicable because the function r(t) is twice differentiable, which implies that its first derivative, r'(t), is continuous.
What is the conclusion about r'(t) being equal to -6 based on the IVT?
-Since r'(0) is less than -6 and r'(3) is greater than -6, by the IVT, there must be some t value between 0 and 3 for which r'(t) equals -6.
How is the value of the integral from 0 to 12 of r'(t) dt approximated?
-The value is approximated using a right Riemann sum with four subintervals, each using the right endpoint value from the table for r'(t) over the respective interval.
What is the rate of change of the volume of the cone with respect to time at t=3 days?
-The rate of change of the volume with respect to time, dv/dt, is calculated using implicit differentiation and the given values for r(t), h(t), and their respective rates of change at t=3 days.
What are the given values for the height and radius of the cone at t=3 days?
-The given values are a radius of 100 cm and a height of 50 cm at t=3 days.
Outlines
📚 AP Calculus Exam Table Problem Overview
This paragraph introduces the AP Calculus exam problem involving an ice sculpture that melts while maintaining a conical shape. The radius of the base of the cone is described by a twice differentiable function r(t), where r is in centimeters and t is in days. The problem provides a table of selected values of r'(t), the rate of change of the radius over a 0 to 12-day interval. The paragraph outlines the steps to approximate r''(8.5) using the average rate of change from 7 to 10 days, emphasizing the importance of not simplifying numerical values unnecessarily due to the pressure of the exam situation.
🔍 Applying the Intermediate Value Theorem
The paragraph discusses the application of the Intermediate Value Theorem (IVT) to determine if there exists a time t between 0 and 3 when r'(t) equals -6. It is established that r' is continuous since r is twice differentiable. By examining the values of r'(0) and r'(3), it is concluded that there must be a t value within the 0 to 3 range where r'(t) equals -6, as the function crosses the value -6 at some point due to the IVT.
🧮 Approximating the Integral with a Right Riemann Sum
This section covers the use of a right Riemann sum with four subintervals to approximate the integral from 0 to 12 of r'(t) dt. The approach involves using the right endpoint values from the table for each subinterval and summing them without simplification. The emphasis is on not simplifying the answer to avoid losing points due to potential errors in simplification.
📏 Calculating the Rate of Change of Volume of a Cone
The final paragraph addresses the calculation of the rate of change of the volume of the cone with respect to time, given the height decreases at a rate of 2 cm per day and specific measurements at t = 3 days. Using implicit differentiation and the formula for the volume of a cone, the rate of change of volume dv/dt is determined. The paragraph highlights the importance of plugging in the given values and applying the units correctly without overcomplicating the simplification process.
Mindmap
Keywords
💡Ice sculpture
💡Twice differentiable function
💡Average rate of change
💡Intermediate Value Theorem (IVT)
💡Right Riemann sum
💡Implicit differentiation
💡Product rule
💡Related rates
💡Volume of a cone
💡Centimeters per day
💡Units of measure
Highlights
The video discusses a table problem from the 2022 AP Calculus exams involving an ice sculpture modeled as a melting cone.
The radius of the base of the cone is given by a twice differentiable function r(t), where t is measured in days.
Part A of the problem involves approximating the second derivative of r at t=8.5 using the average rate of change of r' over the interval from t=7 to t=10.
The average rate of change is calculated as (r'(10) - r'(7)) / (10 - 7), with values from the table used for computation.
The units of measure for the second derivative are centimeters per day per day, emphasizing not to simplify numerical values.
The video explains the use of the Intermediate Value Theorem (IVT) to determine if r'(t) equals -6 for some t between 0 and 3.
Since r is twice differentiable, r' is continuous, allowing the application of IVT.
Values of r'(0) and r'(3) establish that r'(t) must equal -6 for some t between 0 and 3 due to the IVT.
A right Riemann sum with four subintervals is used to approximate the integral of r'(t) from 0 to 12.
The video advises against simplifying the Riemann sum, to avoid losing points due to potential errors.
The height of the cone decreases at a rate of 2 cm/day, and the problem involves finding the rate of change of the cone's volume with respect to time.
The volume of the cone is given by the formula V = π/3 * r^2 * h, and the rate of change of volume is found using implicit differentiation.
The values for r(t=3), h, and dr/dt are found using the given information and the table provided.
The final expression for the rate of change of volume dv/dt is calculated using the values obtained from the problem.
The video emphasizes the importance of including units in the final answer and advises against unnecessary simplification.
The final answer for dv/dt is approximately -70000π/3 cubic centimeters per day, showcasing the application of related rates in calculus.
The presenter plans to cover the rest of the questions in a subsequent video and wishes viewers good luck.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: