2022 AP Calculus AB BC Free Response #4
TLDRThe video script discusses a mathematical problem involving an ice sculpture that melts in a conical shape. The radius of the cone's base is represented by a twice differentiable function, r(t), where r is measured in centimeters and t in days. The problem involves calculating the approximate second derivative of r(t) at t=8.5 using a secant line approach, and determining if there exists a time when the first derivative, r'(t), equals -6. By applying the Intermediate Value Theorem, it's concluded that such a time exists between 0 and 3 days. The script then moves on to approximate the integral of r'(t) over a given interval using a right Riemann sum with four sub-intervals. Finally, it calculates the rate of change of the cone's volume with respect to time, given the height and radius of the cone at a specific time, using the formula for the volume of a cone and differentiating it with respect to time. The presenter also acknowledges the possibility of arithmetic errors due to fatigue.
Takeaways
- 📊 The ice sculpture's melting can be modeled as a conical shape that maintains its form as it decreases in size.
- ⏱️ Time, denoted as 't', is measured in days, and the radius of the base of the cone, denoted as 'r(t)', is a twice differentiable function in centimeters.
- 📌 The rate of change of the radius, 'r'(t), is given by 'r' prime, measured in centimeters per day.
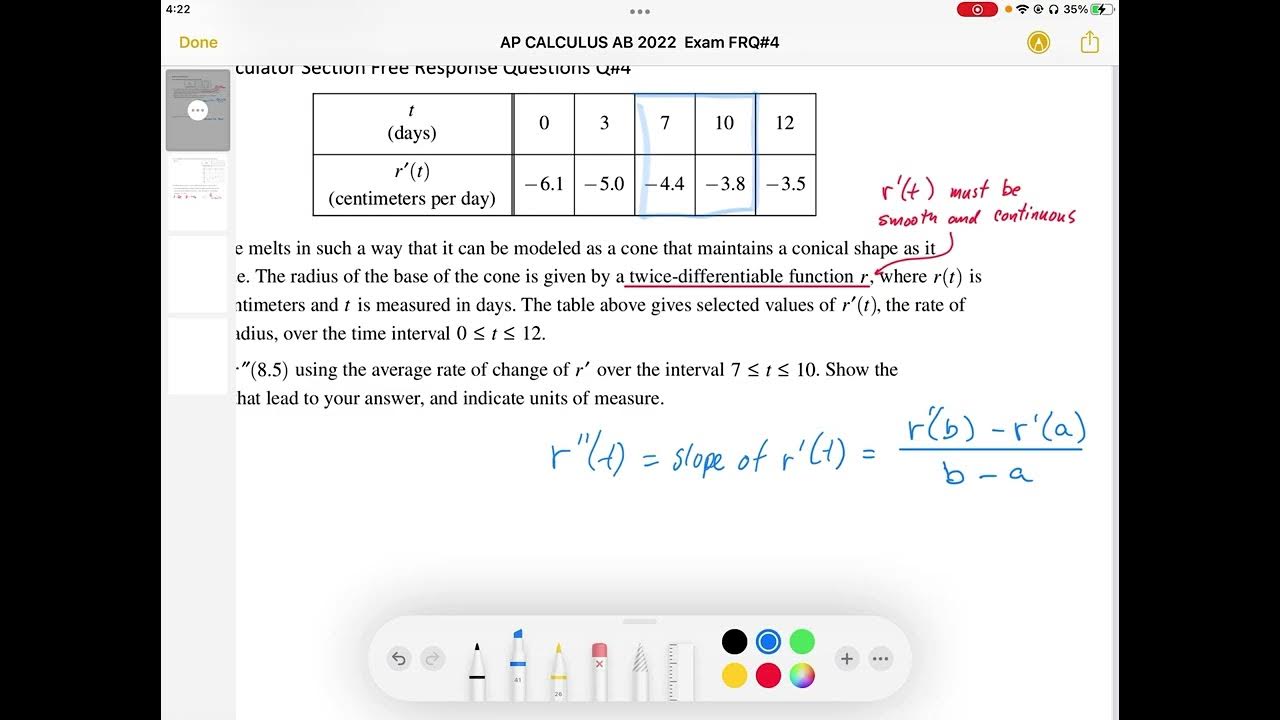
- 🔍 An approximation of the second derivative, 'r' double prime, at t=8.5 is calculated using a secant line method.
- 🔢 The calculation of 'r' double prime at t=8.5 involves a comparison of 'r' prime values at t=7 and t=10, resulting in a value of approximately -0.2 centimeters per day squared.
- 📉 The existence of a time 'c' where 'r' prime equals negative six is confirmed using the intermediate value theorem, with 'c' being between 0 and 3 days.
- 🧮 A right Riemann sum with four sub-intervals is used to approximate the value of the integral of 'r' prime over a certain interval, resulting in a value of -51 centimeters.
- 📐 The height of the cone decreases at a rate of negative two centimeters per day at t=3 days.
- 🔨 The volume of the cone, 'V', is given by the formula V = (1/3)πr^2h, and the rate of change of volume with respect to time, dv/dt, is derived using the product rule.
- 📏 At t=3 days, with a radius of 100 centimeters and a height of 50 centimeters, the rate of change of the cone's volume with respect to time is calculated to be -(70000π/3) cubic centimeters per day.
- 🤔 The speaker acknowledges the possibility of arithmetic errors in their calculations due to fatigue.
Q & A
What is the shape of the ice sculpture as it melts?
-The ice sculpture melts in such a way that it can be modeled as a cone, maintaining a conical shape as it decreases in size.
How is the radius of the base of the cone described in the script?
-The radius of the base of the cone is described by a twice differentiable function, r(t), where r is measured in centimeters and t is measured in days.
What does r'(t) represent in the context of the problem?
-r'(t) represents the rate of change of the radius of the base of the cone, measured in centimeters per day.
How is the approximate value of r''(8.5) calculated?
-The approximate value of r''(8.5) is calculated using the secant line slope over the interval from t=7 to t=10, which is r'(10) - r'(7) divided by (10 - 7).
What is the conclusion about the existence of a time when r'(t) equals negative six?
-By observing the values of r'(t) and applying the intermediate value theorem, it is concluded that there must exist a time c between 0 and 3 when r'(c) equals negative six.
Why is r'(t) considered continuous?
-Since r(t) is twice differentiable, it implies that r(t) and its first derivative r'(t) are continuous. Continuity of r'(t) also follows from the fact that it is differentiable.
What is the purpose of using the right Riemann sum with four sub-intervals?
-The right Riemann sum with four sub-intervals is used to approximate the value of the integral of r'(t) over the given time intervals, as indicated by the table in the script.
What does the integral of r'(t) represent?
-The integral of r'(t) represents the total change in the radius of the base of the cone over the given time period, measured in centimeters.
How is the rate of change of the volume of the cone with respect to time, dv/dt, calculated?
-The rate of change of the volume of the cone with respect to time, dv/dt, is calculated using the formula for the derivative of the volume of a cone, which involves the product rule applied to r^2 and h.
What are the given values for the radius and height of the cone at time t equals three days?
-At time t equals three days, the radius (r) of the cone is 100 centimeters, and the height (h) is 50 centimeters.
What is the final expression for the rate of change of the volume of the cone at t equals three days?
-The final expression for the rate of change of the volume of the cone at t equals three days is (1/3)π * (10,000 * -2 + 2 * 100 * -5), which simplifies to -70,000π/3 cubic centimeters per day.
Outlines
📏 Modeling Ice Sculpture Melting as a Cone
This paragraph discusses modeling the melting of an ice sculpture as a cone and the given function representing its radius over time. It explains how to approximate the second derivative of the radius at a given point, determine when the rate of change of the radius is negative six, and use the right Riemann sum to approximate a value.
🔍 Finding the Rate of Change of Volume
This section focuses on finding the rate of change of the volume of the cone as it melts. It utilizes the formula for the volume of a cone, calculates the derivative with respect to time using the product rule, and evaluates it at a specific time. Finally, it provides the rate of change of volume at that time.
Mindmap
Keywords
💡Ice sculpture
💡Cone
💡Twice differentiable function
💡Radius
💡Derivative
💡Secant line slope
💡Intermediate Value Theorem
💡Riemann sum
💡Product rule
💡Volume of a cone
💡Rate of change
Highlights
An ice sculpture melts in a conical shape, with the radius of the base given by a twice differentiable function.
The rate of change of the radius is given in centimeters per day, and the radius itself is measured in centimeters.
The derivative of the radius function, r'(t), is used to approximate r''(8.5) using secant line slope method.
The value of r''(8.5) is approximated to be centimeters per day squared, indicating the rate of change of the radius over time.
The existence of a time t where r'(t) equals negative six is confirmed using the intermediate value theorem.
The conditions for the intermediate value theorem are discussed, including the continuity of r'(t).
A right Riemann sum with four sub-intervals is used to approximate the value of an integral.
The calculation of the Riemann sum results in a value of negative 44 minus 51 centimeters.
The height of the cone decreases at a rate of negative two centimeters per day at time t equals three days.
The radius and height of the cone at t equals three days are given as 100 centimeters and 50 centimeters, respectively.
The rate of change of the volume of the cone with respect to time, dv/dt, is derived using the product rule.
The derivative dr/dt at three days is identified as negative five from the table provided.
The final calculation for dv/dt results in a value of negative seventy thousand pi over three cubic centimeters per day.
The importance of accurate arithmetic in mathematical calculations is emphasized, acknowledging the potential for errors.
The process involves the application of differentiation and integration to real-world problems, specifically the melting of an ice sculpture.
The use of the intermediate value theorem to find a specific value of a function that meets certain criteria.
The application of the Riemann sum to approximate the value of a definite integral, demonstrating a fundamental concept in calculus.
The practical application of calculus in determining the rate of change of physical quantities, such as the volume of a melting ice sculpture.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: