Estimating areas using trapezoidal rule [IB Maths AI SL/HL]
TLDRThe video script provides a comprehensive guide on how to estimate the area under a curve using the trapezoidal rule, a method particularly useful when the equation of the curve is unknown. The presenter begins by explaining the concept of a trapezoid and its area calculation, then transitions into applying this concept to a curve by dividing it into several trapezoidal sections. The key insight is that the 'height' in this context refers to the x-values between data points, not the vertical height. The formula for the trapezoidal rule is broken down, emphasizing that it involves summing the areas of individual trapezoids, each calculated as half the height times the sum of the y-values (data points) of the trapezoid's parallel sides. The presenter illustrates the process with an example using six data points, resulting in five trapezoids, and demonstrates how to apply the formula to find the approximate area under the curve. The summary clarifies that despite the formula's complexity, the process involves simple arithmetic once the data points and trapezoids are identified, making it an accessible method for area estimation in calculus.
Takeaways
- 📐 **Trapezoidal Rule Overview**: The trapezoidal rule is a method to estimate the area under a curve when the equation of the curve is not known, using a series of trapezoids.
- 📈 **Integrals and Data Points**: Instead of using the equation of a function, the trapezoidal rule uses data points to estimate areas, which is useful when the function's equation is not available.
- 🔍 **Breaking Down the Curve**: The process involves breaking the area under the curve into equal length segments and drawing trapezoids to approximate the area.
- 🤸 **Trapezoid Geometry**: A trapezoid has two parallel sides of potentially different lengths and a height, which in this context is the distance between the parallel sides.
- 📏 **Area of a Trapezoid**: The area of a trapezoid is given by the formula (1/2) * (a + b) * h, where 'a' and 'b' are the lengths of the parallel sides and 'h' is the height.
- ✅ **Turning Trapezoids**: The trapezoids used in the trapezoidal rule are turned on their side, so the 'height' refers to the x-value difference between data points.
- 📉 **Estimating with Trapezoids**: The area under the curve is estimated by calculating the area of each trapezoid and summing them up, which gives an approximation of the total area.
- 📌 **Data Points vs. Trapezoids**: There is always one less trapezoid than the number of data points, so if there are 'n' data points, there will be 'n-1' trapezoids.
- 🔢 **Equal Heights**: In the trapezoidal rule, all trapezoids are considered to have the same 'height', which is calculated as the difference between the maximum and minimum x-values divided by the number of trapezoids.
- 🧮 **General Formula**: The general formula for the trapezoidal rule is given by (1/2) * h * (y0 + yn + 2*(y1 + y2 + ... + yn-1)), where 'h' is the height and 'y' values are the data points.
- 📚 **Understanding the Formula**: The formula can seem complex, but it simplifies to the first y-value, the last y-value, and twice the sum of all intermediate y-values, multiplied by the height.
Q & A
What is the trapezoidal rule used for?
-The trapezoidal rule is used to estimate the area under a curve, especially when the equation of the curve is not known, by using a series of trapezoids to approximate the region.
How does the trapezoidal rule relate to integral calculus?
-The trapezoidal rule is a numerical method that approximates the definite integral of a function, which is the exact area under the curve of the function over a given interval.
What is the formula for the area of a trapezoid?
-The area of a trapezoid is given by the formula (1/2) * (a + b) * h, where 'a' and 'b' are the lengths of the parallel sides and 'h' is the height of the trapezoid.
Why do we turn the trapezoids on their side when applying the trapezoidal rule?
-Turning the trapezoids on their side allows us to use the x-values as the 'height' of the trapezoids in the context of the curve, making it easier to apply the formula when the y-values (function values) are known at specific x-values.
How many trapezoids are used when applying the trapezoidal rule to n data points?
-When applying the trapezoidal rule to n data points, you use n-1 trapezoids, as each trapezoid is formed between consecutive data points.
What is the significance of the 'height' in the context of the trapezoidal rule for numerical integration?
-In the context of the trapezoidal rule, the 'height' (h) is the difference between the x-values of two consecutive data points, which is used to determine the width of each trapezoid.
How is the height (h) calculated when using the trapezoidal rule with equally spaced data points?
-When the data points are equally spaced, the height (h) is calculated as the difference between the maximum and minimum x-values (b - a) divided by the number of trapezoids (n).
What is the general formula for the area under a curve using the trapezoidal rule with n trapezoids?
-The general formula is (1/2) * h * (y0 + yn + 2 * Σ(yi for i = 1 to n-1)), where y0 is the first y-value, yn is the last y-value, and the sum includes all intermediate y-values.
Why does the first and last term in the trapezoidal rule formula not get multiplied by 2?
-The first and last terms represent the y-values at the endpoints of the interval, which only contribute to one trapezoid each, hence they are not multiplied by 2, unlike the intermediate y-values.
What is the practical application of the trapezoidal rule?
-The trapezoidal rule is used in numerical analysis to estimate areas under curves that cannot be integrated analytically, which is useful in various fields such as physics, engineering, and economics.
How does the trapezoidal rule help in approximating the area under a curve when only data points are available?
-The trapezoidal rule allows us to approximate the area by breaking the region under the curve into trapezoids, each with a known height and average y-value, which can be calculated from the given data points.
Outlines
📐 Introduction to the Trapezoidal Rule for Area Calculation
The speaker begins by introducing the trapezoidal rule, a method for estimating the area under a curve when the equation is unknown, using data points instead. They use a humorous reference to Admiral Akbar from Star Wars to explain the concept of a trapezoid, which is a shape with two parallel sides of potentially different lengths. The area under a curve can be approximated by dividing it into trapezoids of equal length and summing their areas. The formula for the area of a trapezoid is also introduced, which is half the product of the sum of the lengths of the parallel sides and the height.
📈 Applying the Trapezoidal Rule with Data Points
The video script explains how to apply the trapezoidal rule using a set of data points. It emphasizes that the number of trapezoids used is always one less than the number of data points provided. The concept of 'height' in the context of the trapezoidal rule is clarified to mean the difference in the x-values (b-a) divided by the number of trapezoids (n). Each trapezoid's area is calculated using the formula half times the height times the sum of the y-values of the parallel sides. The process is demonstrated with an example using five data points, resulting in four trapezoids.
🧮 Simplifying the Trapezoidal Rule Formula
The speaker simplifies the complex formula for the trapezoidal rule that might be found in a formula booklet. They explain that the formula involves the first and last y-values singly, while all the intermediate y-values are doubled and summed. The height (h) is defined as the difference between the maximum and minimum x-values divided by the number of trapezoids (n). The general formula for the area under the curve using the trapezoidal rule is provided, and the speaker reassures that despite its complexity, it can be understood by breaking it down into its components.
📝 Using the Trapezoidal Rule Formula with a Real Example
In the final paragraph, the speaker applies the trapezoidal rule formula to a real example with six data points, resulting in five trapezoids. They calculate the height (h) as the difference between the maximum and minimum x-values, which in this case is 1 since the x-values are equally spaced. The area under the curve is approximated by summing the areas of the individual trapezoids, using the formula provided. The calculation is demonstrated step by step, resulting in an approximate area of 6.3. The speaker emphasizes the importance of understanding the formula and the process rather than being intimidated by its complexity.
Mindmap
Keywords
💡Trapezoidal Rule
💡Integral
💡Data Points
💡Trapezoid
💡Area Estimation
💡Height (h)
💡Numerical Integration
💡Function
💡Approximation
💡Calculus
💡Graph
Highlights
The trapezoidal rule is introduced as a method to find the area under a curve when the equation of the curve is unknown.
The concept of a trapezoid with two parallel sides of different lengths is explained, with a focus on the 'height' of the trapezoid.
The area under a curve can be estimated by dividing it into trapezoids of equal length and summing their areas.
The formula for the area of a trapezoid is provided and explained in the context of the trapezoidal rule.
A practical example demonstrates how to use the trapezoidal rule to estimate the area under a curve given a set of data points.
The importance of the number of data points and trapezoids is emphasized, with a rule that the number of trapezoids is always one less than the number of data points.
The height of each trapezoid in the approximation is determined by the difference between the maximum and minimum x values, divided by the number of trapezoids.
The general formula for the trapezoidal rule is presented, showing how to sum the areas of individual trapezoids to estimate the total area under the curve.
The process of calculating the area using the trapezoidal rule is demonstrated step by step, emphasizing the pattern of terms in the formula.
The formula's complexity is addressed, with reassurance that understanding the pattern makes it manageable.
A real-world example is used to illustrate the application of the trapezoidal rule formula, showing how to calculate the area under a curve with given data points.
The calculation process is simplified by recognizing that the height (h) is the same for all trapezoids in the approximation.
The final area calculation is demonstrated, showing how the formula's terms are summed to provide an estimate of the area under the curve.
The presenter emphasizes that despite its initial complexity, the trapezoidal rule formula can be decoded and applied systematically.
The importance of careful observation and understanding of the formula's structure is highlighted for successful application of the trapezoidal rule.
The presenter reassures that the trapezoidal rule, while it may seem daunting at first, is a manageable method for estimating areas under curves.
The final calculated area using the trapezoidal rule is presented, demonstrating the practical application of the method.
Transcripts
Browse More Related Video

Learn how to use the trapezoidal rule with 4 sub intervals

The Trapezoid Rule for Approximating Integrals

Trapezoidal sums | Accumulation and Riemann sums | AP Calculus AB | Khan Academy

Worked example: finding a Riemann sum using a table | AP Calculus AB | Khan Academy

AP Calculus AB: Lesson 6.2 Riemann and Trapezoidal Sums
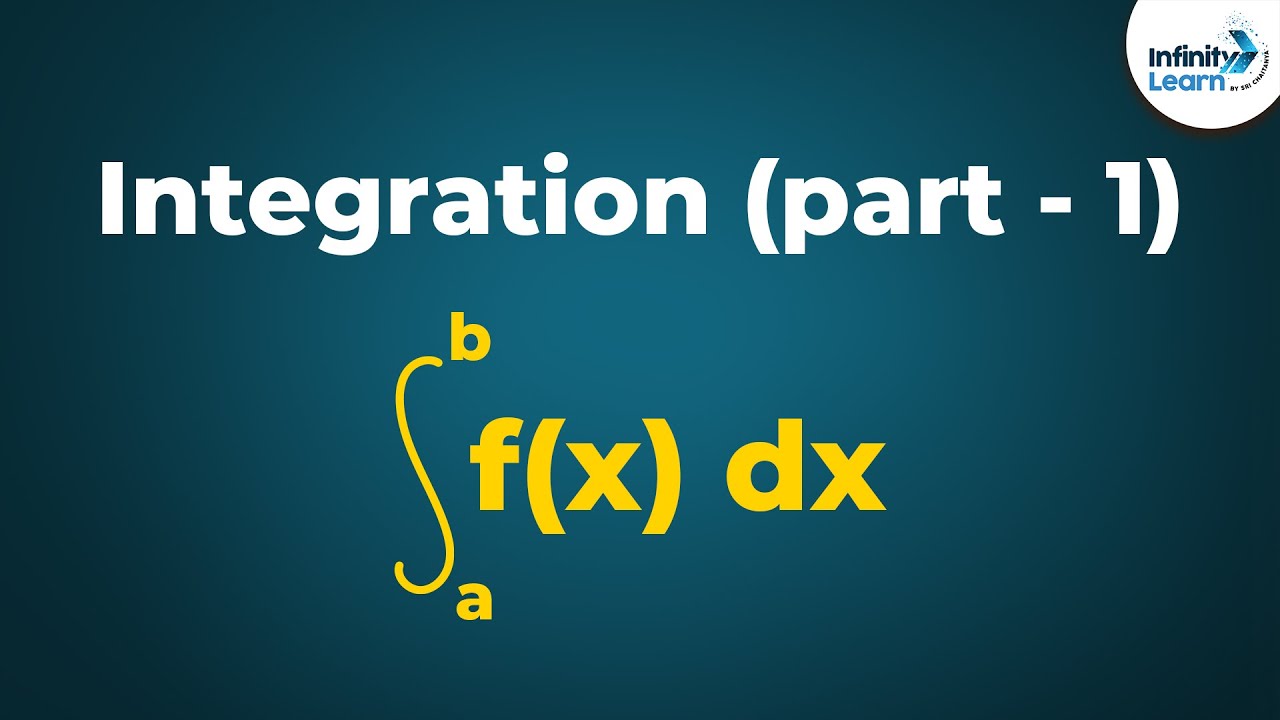
Calculus - Lesson 13 | Integral of a Function | Don't Memorise
5.0 / 5 (0 votes)
Thanks for rating: