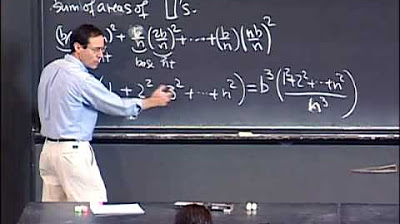Definite Integrals — Topic 88 of Machine Learning Foundations
TLDRThe video script introduces the concept of definite integrals, contrasting them with indefinite integrals by emphasizing that definite integrals calculate the area under a curve within a specific range, rather than the entire area. The script guides viewers through an example using the function y = (1/2)x, integrating it from x = 1 to x = 2. It demonstrates the process of finding the indefinite integral first, then applying it to find the desired area by subtracting the integral evaluated at the lower limit from that at the upper limit, resulting in an area of three-quarters of a squared unit. The video concludes with an invitation to learn how to calculate definite integrals in Python and to engage with further content through subscription, liking, commenting, and following on social media.
Takeaways
- 📊 The key difference between indefinite and definite integrals is that definite integrals calculate the area under a curve within a specific range, denoted by x1 to x2.
- 📈 Definite integrals are denoted by the integral symbol with the range of integration (x1 to x2) written at the bottom and top of the symbol, respectively.
- 🧮 To calculate a definite integral, you first find the indefinite integral of the function using standard integration techniques.
- 📐 The example in the script uses the function y = (1/2)x, and the area of interest is between x = 1 and x = 2.
- 🔢 The constant multiple rule allows you to ignore constants when integrating, and the power rule is applied to integrate x to the power of one, resulting in x squared divided by two.
- ➕ After applying the power rule, remember to reintroduce the ignored constant (in this case, 1/2) and include the constant of integration (C).
- 🔴 To find the area under the curve between two points, substitute the upper and lower limits of integration into the indefinite integral and calculate the difference.
- 🔵 The constant of integration (C) cancels out when subtracting the two areas, as it is present in both calculations.
- 📉 The area under the curve between x = 1 and x = 2 for the function y = (1/2)x is calculated to be three-quarters of a squared unit.
- 💻 The script also mentions that the next step is to learn how to calculate definite integrals using Python.
- 📚 A comprehension exercise will be provided to test knowledge on definite integrals.
- 📺 The presenter encourages viewers to subscribe to the channel and engage with the content by liking, commenting, and signing up for the email newsletter.
Q & A
What is the primary difference between indefinite integrals and definite integrals?
-The primary difference is that indefinite integrals provide the family of functions that are antiderivatives of the integrand, while definite integrals calculate the specific area under the curve of a function between two points, denoted as x1 and x2.
How is the notation for definite integrals different from that of indefinite integrals?
-The notation for definite integrals includes the limits of integration, which are the start and end points of the range, written at the bottom and top of the integral symbol, respectively. Indefinite integrals do not have these limits.
What is the first step in calculating a definite integral?
-The first step in calculating a definite integral is to compute the indefinite integral of the function using techniques such as the constant multiple rule and the power rule.
What is the function that was used as an example in the video?
-The function used as an example in the video is y = (1/2)x.
What is the range of x values for which the definite integral was calculated in the example?
-The range of x values for which the definite integral was calculated is from x = 1 to x = 2.
How is the area under a curve between two points calculated using definite integrals?
-The area under a curve between two points is calculated by finding the difference between the values of the indefinite integral evaluated at the upper limit and the lower limit of integration.
What is the result of the definite integral for the function y = (1/2)x from x = 1 to x = 2?
-The result of the definite integral for the given function and range is 3/4 square units.
Why is the constant of integration (C) not included in the final answer when calculating a definite integral?
-The constant of integration (C) is not included in the final answer because when calculating definite integrals, the constant cancels out when subtracting the value of the integral at the lower limit from the value at the upper limit.
What is the significance of the constant multiple rule in the context of the example provided?
-The constant multiple rule allows us to separate the constant factor from the variable when integrating, which simplifies the integration process. In the example, the constant 1/2 was ignored initially and then reintegrated into the final result.
How does the power rule apply to the integration of x in the example?
-According to the power rule, when integrating x to the power of 1, you add 1 to the power, resulting in x^2, and then divide by the new power. In the example, this results in (x^2)/2.
What is the next step after calculating a definite integral by hand, as mentioned in the video?
-The next step mentioned in the video is to learn how to calculate definite integrals using Python and then to engage in a comprehension exercise to test the understanding of definite integrals.
How can viewers stay updated with the content from the tutorial series?
-Viewers can stay updated by subscribing to the channel, signing up for the email newsletter at johncrone.com, connecting on LinkedIn, and following on Twitter.
Outlines
📐 Understanding Definite Integrals
This paragraph introduces the concept of definite integrals, contrasting them with indefinite integrals. It emphasizes that definite integrals focus on the area under a curve within a specific range, denoted by x1 to x2. The notation for definite integrals is explained, which includes the range of integration at the bottom and top of the integral symbol. An example is provided to illustrate the calculation of a definite integral for the function y = (1/2)x, with the area of interest from x = 1 to x = 2. The process involves first finding the indefinite integral using the power rule and constant multiple rule, then applying the limits of integration to find the desired area. The indefinite integral of y = (1/2)x is found to be (1/4)x^2 + C, and by substituting the limits of integration, the area under the curve is determined.
📊 Calculating Definite Integrals: A Visual Approach
The second paragraph delves into the calculation of definite integrals using a visual approach. It outlines the process of finding the area under a curve by subtracting the area of a smaller triangle from a larger one. The example continues with the function y = (1/2)x, with the focus on the area between x = 1 and x = 2. The areas of the triangles formed by the curve and the x-axis are calculated by substituting the respective x-values into the indefinite integral. The smaller triangle area is found to be 1/4 square unit, and the larger triangle area is 1 square unit. By subtracting the smaller area from the larger one, the definite integral's area is determined to be 3/4 square unit. The paragraph concludes with an invitation to learn how to calculate definite integrals in Python and to engage in a comprehension exercise to test the understanding of definite integrals. The speaker also encourages viewers to subscribe, like, comment, and follow for more content.
Mindmap
Keywords
💡Definite Integrals
💡Indefinite Integrals
💡Integration Range
💡Constant Multiple Rule
💡Power Rule
💡Integration Operator
💡Area Under the Curve
💡Constant of Unknown Value (C)
💡Substitution
💡Visual Approach
💡Python
Highlights
The video introduces the concept of definite integrals, contrasting them with indefinite integrals by focusing on a specific range rather than the entire area under a curve.
The definite integral is denoted with the start and end of the range at the bottom and top of the integral symbol, respectively.
An example is provided to illustrate the calculation of a definite integral, using the function y = (1/2)x.
The area of interest is between x = 1 and x = 2, which is calculated using the definite integral.
The first step in calculating a definite integral is to compute the indefinite integral using the power rule and constant multiple rule.
The indefinite integral of (1/2)x is found to be (1/4)x^2 + C, where C is the constant of integration.
To find the area under the curve, the values of the indefinite integral at the limits of integration (x = 1 and x = 2) are evaluated.
The area under the curve from x = 1 to x = 2 is determined by subtracting the value of the integral at x = 1 from the value at x = 2.
The constant of integration (C) cancels out when subtracting the two areas, simplifying the calculation.
The final calculated area under the curve between x = 1 and x = 2 is three-quarters of a squared unit.
The video demonstrates a visual approach to calculating definite integrals, making the process more accessible and understandable.
Upcoming content will include how to calculate definite integrals using Python, providing a practical application of the concept.
A comprehension exercise is promised to test the viewer's understanding of definite integrals.
The presenter encourages viewers to subscribe to the channel for the next video in the series.
The presenter invites viewers to engage with the content by liking, commenting, and subscribing to the email newsletter.
Professional networking is encouraged through LinkedIn, with a mention for viewers to identify themselves as part of the machine learning foundation series audience.
The presenter also has a presence on Twitter, offering another platform for viewers to follow and engage with the content.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: