Cosine Wave | Simple Explanation on a Giant or Ferris Wheel | Trigonometry | Learnability

Waves - Sine, Cosine, and Tangent | Trigonometry - Rose University
5 Dec 202004:52
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides an engaging explanation of the cosine wave, a mathematical function that oscillates similarly to a sine wave but starts from a different position. It uses the analogy of a giant wheel to illustrate the concept, where the vertical movement of a point on the wheel over time forms the shape of a cosine wave. The prefix 'co' in cosine stands for 'complementary,' referring to angles that sum up to 90 degrees. The script explains that the cosine function is derived from the complementary angles in a right-angled triangle, and it complements the sine function in phase and amplitude. The video aims to clarify the meaning of 'co' in cosine and how the cosine wave's shape is determined by the complementary relationship between angles in a right-angled triangle.

Takeaways
  • 🍦 The cosine wave is similar to a sine wave but starts at a different position, resulting in a distinct shape.
  • 🔵 The prefix 'co' in cosine stands for 'complementary', which relates to angles that sum up to 90 degrees.
  • ⏱️ A cosine wave's shape can be visualized by tracking the vertical movement of a point on a rotating wheel over time.
  • 📈 The graph of the cosine wave is formed by plotting the vertical position of a point against a horizontal time axis.
  • 🔄 Both sine and cosine waves oscillate back and forth from an equilibrium position to a maximum amplitude.
  • 📐 In the context of right-angle triangles, complementary angles add up to 90 degrees, which is the basis for the term 'cosine'.
  • 🎢 The example of a giant wheel is used to illustrate the concept of complementary angles and the cosine function.
  • 🔴 At 45 degrees, the sine of 45 is complementary to the cosine of 45, showcasing the relationship between sine and cosine at complementary angles.
  • 🟢 When the angle is 60 degrees, the sine of 60 is complementary to the cosine of 30, demonstrating the cosine function's complementary nature.
  • 🌀 For every angle 'a', there is a complementary angle 'b' such that 'a' plus 'b' equals 90 degrees, which is central to understanding the cosine function.
  • 📚 The video aims to educate viewers on the concept of cosine waves and their relationship to complementary angles in trigonometry.
Q & A

  • What is the shape of a cosine wave?

    -A cosine wave is similar to a sine wave but starts at a different position on the graph, oscillating back and forth from the equilibrium position vertically.

  • How does the prefix 'co' in cosine affect the shape of the wave?

    -The prefix 'co' stands for complementary and indicates that the cosine wave is a complement to the sine wave, starting from a different phase position.

  • What does the term 'complementary' mean in the context of angles?

    -Complementary refers to two angles that sum up to 90 degrees or a right angle. If angle A and angle B add up to 90 degrees, A complements B and vice versa.

  • How long does it take for the giant wheel to complete one rotation in the given example?

    -In the example provided, the giant wheel takes 20 minutes to complete one full rotation.

  • What is the position of the blue square on the giant wheel after 10 minutes?

    -After 10 minutes, the blue square is at the bottom of the giant wheel.

  • How is the shape of the cosine wave determined when plotting the vertical movement of the blue square over time?

    -The shape of the cosine wave is determined by plotting the vertical movement of the blue square against a horizontal time axis, showing the up and down oscillation from the equilibrium position.

  • What is the amplitude of a sine or cosine wave?

    -The amplitude of a sine or cosine wave is the maximum extent of its oscillation from the equilibrium position in either direction.

  • How does the cosine wave relate to the right angle triangle formed by the rotation of the giant wheel?

    -The cosine wave relates to the right angle triangle by representing the complementary angle to the angle formed by the rotation of the giant wheel. For example, if the angle is 45 degrees, the cosine of that angle is the complementary angle, which is also 45 degrees.

  • What is the relationship between the sine and cosine of complementary angles?

    -The sine and cosine of complementary angles are related such that the sine of one angle is equal to the cosine of its complementary angle, and vice versa. For example, sine of 45 degrees equals cosine of 45 degrees.

  • Why is the cosine wave shown in blue in the video?

    -The cosine wave is shown in blue to differentiate it from the sine wave, which is shown in red. This color distinction helps to visually compare the two types of waves.

  • What is the significance of the right angle triangle in understanding the cosine wave?

    -The right angle triangle is significant because it helps to visualize the complementary relationship between angles and their corresponding sine and cosine values, especially when considering the rotation of the giant wheel.

  • How does the video script help in understanding the concept of cosine waves?

    -The video script uses the analogy of a giant wheel and a blue square moving on it to illustrate the concept of cosine waves. It explains how the vertical movement of the square over time forms the cosine wave shape and relates this to the concept of complementary angles in trigonometry.

Outlines
00:00
📊 Understanding the Cosine Wave

The video begins by introducing the cosine wave, which is visually similar to a sine wave but with a different starting position. It explains that the prefix 'co' in cosine stands for 'complementary,' referring to angles that sum up to 90 degrees. The video uses an analogy of a giant wheel to illustrate how the cosine wave gets its shape. As the wheel rotates, the vertical movement of a point on the wheel is plotted against time, creating the cosine wave pattern. The video emphasizes that cosine waves, like sine waves, oscillate between a maximum amplitude and an equilibrium position, but they start from a different point.

Mindmap
Keywords
💡Cosine Wave
A cosine wave is a type of periodic function that oscillates between -1 and 1, similar to a sine wave but with a phase shift. In the video, it is described as having a shape akin to an ice cream cone and is shown in blue. It is used to illustrate the concept of complementary angles in trigonometry and is derived from the vertical movement of a point on a rotating wheel, which is a key part of the video's explanation of the concept.
💡Sine Wave
A sine wave is a continuous wave that oscillates between -1 and 1 and is often used to represent periodic phenomena. In the video, the sine wave is mentioned in contrast to the cosine wave, with the prefix 'co' in cosine indicating a complementary relationship. The sine wave is shown in red and is used to demonstrate the concept of oscillation, which is central to the video's discussion of wave shapes.
💡Phase Shift
Phase shift refers to a change in the timing of a repeating waveform, such that it is shifted forward or backward in time. The video explains that while sine and cosine waves oscillate similarly, the cosine wave has a phase shift that starts it at a different position than the sine wave. This concept is crucial for understanding the difference in shape between the two types of waves.
💡Giant Wheel
The giant wheel is used as a metaphor in the video to help visualize the movement of a point on the wheel, which corresponds to the cosine wave. The wheel's rotation and the position of the blue square on it are used to explain the vertical movement that results in the cosine wave's shape. This analogy is central to the video's narrative for teaching the concept of cosine waves.
💡Amplitude
Amplitude is the maximum extent of a wave's displacement from its equilibrium or central position. In the video, amplitude is mentioned as the maximum amount that sine and cosine waves oscillate from their equilibrium position. It is a fundamental concept in understanding the behavior of these waves and is illustrated by the up and down movement of the blue square on the giant wheel.
💡Complementary Angles
Complementary angles are two angles that add up to 90 degrees. The video uses the concept of complementary angles to explain the prefix 'co' in cosine. It is illustrated with examples of angles on a right-angled triangle, where one angle complements another to make a right angle. This concept is integral to understanding the relationship between sine and cosine functions.
💡Right Angle Triangle
A right angle triangle is a triangle in which one of the angles is exactly 90 degrees. The video uses right angle triangles to demonstrate the concept of complementary angles and how they relate to the cosine function. The lengths of the sides of these triangles and the angles between them are central to the explanation of how the cosine wave is derived from the rotation of the giant wheel.
💡Equilibrium Position
The equilibrium position is the central or balanced position in a system, from which oscillations or movements occur. In the context of the video, the equilibrium position refers to the center point from which the cosine and sine waves oscillate. It is a key concept in understanding the behavior of these waves and how they are represented on a graph.
💡Horizontal Axis
The horizontal axis in a graph represents one of the two fundamental dimensions, typically used to plot time or another independent variable. In the video, the horizontal axis is used to represent the time dimension as the giant wheel rotates. It is essential for plotting the cosine wave and showing how the vertical movement of the blue square translates into the wave's shape.
💡Vertical Movement
Vertical movement refers to the upward or downward motion, particularly in the context of plotting graphs. The video describes how the vertical movement of the blue square on the giant wheel is plotted against the horizontal time axis to form the cosine wave. This concept is vital for visualizing how the shape of the cosine wave is derived from the physical movement of a point on the wheel.
💡Prefix 'Co'
The prefix 'co' is short for 'complementary' and is used in the term 'cosine' to indicate a relationship to the sine function. In the video, it is explained that the prefix signifies that the cosine function is complementary to the sine function, meaning that they are related through the concept of complementary angles. This is a crucial part of understanding the naming and the mathematical relationship between sine and cosine.
Highlights

Cosine wave is similar to a sine wave but has a different shape due to the prefix 'co'.

The prefix 'co' in cosine stands for 'complementary', referring to two angles that add up to 90 degrees.

The video uses a giant rotating wheel analogy to explain the cosine wave shape.

The blue square's vertical movement on the giant wheel is plotted on a time axis to form the cosine wave.

A cosine wave oscillates back and forth from the equilibrium position, similar to a sine wave but starting at a different position.

Complementary angles are two angles that add up to 90 degrees, and one can be called the complement of the other.

In right angle triangles, any two angles that are not the right angle are complementary.

The shape of the right angle triangle formed by the wheel's rotation changes as the black square moves.

At 45 degrees, the sine of 45 is complement to the angle, which is why it's called cosine 45.

At 60 degrees, the sine of 60 is complement to the angle, which corresponds to the cosine of 30 degrees.

The concept of complementary angles is used to explain the relationship between sine and cosine at different positions on the wheel.

The amplitude of the sine wave at a certain angle is equal to the amplitude of the cosine wave at its complementary angle.

The prefix 'co' in cosine signifies the complementary nature of the angle to the sine function.

The video provides a visual and intuitive explanation of the cosine wave and its relationship with the sine wave.

Understanding the concept of complementary angles is key to grasping the meaning of cosine.

The video uses the giant wheel analogy to make the concept of cosine more accessible and easier to visualize.

The video concludes by emphasizing the importance of continuous learning in understanding mathematical concepts.

Transcripts

Browse More Related Video

Tangent Wave | Tan Function | Trigonometry | Explanation on a Giant Wheel | Slope | Learnability

Cofunction Identities Examples & Practice Problems Trigonometry

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

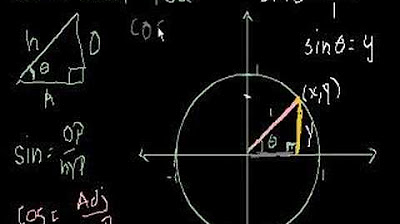
Unit Circle Definition of Trig Functions

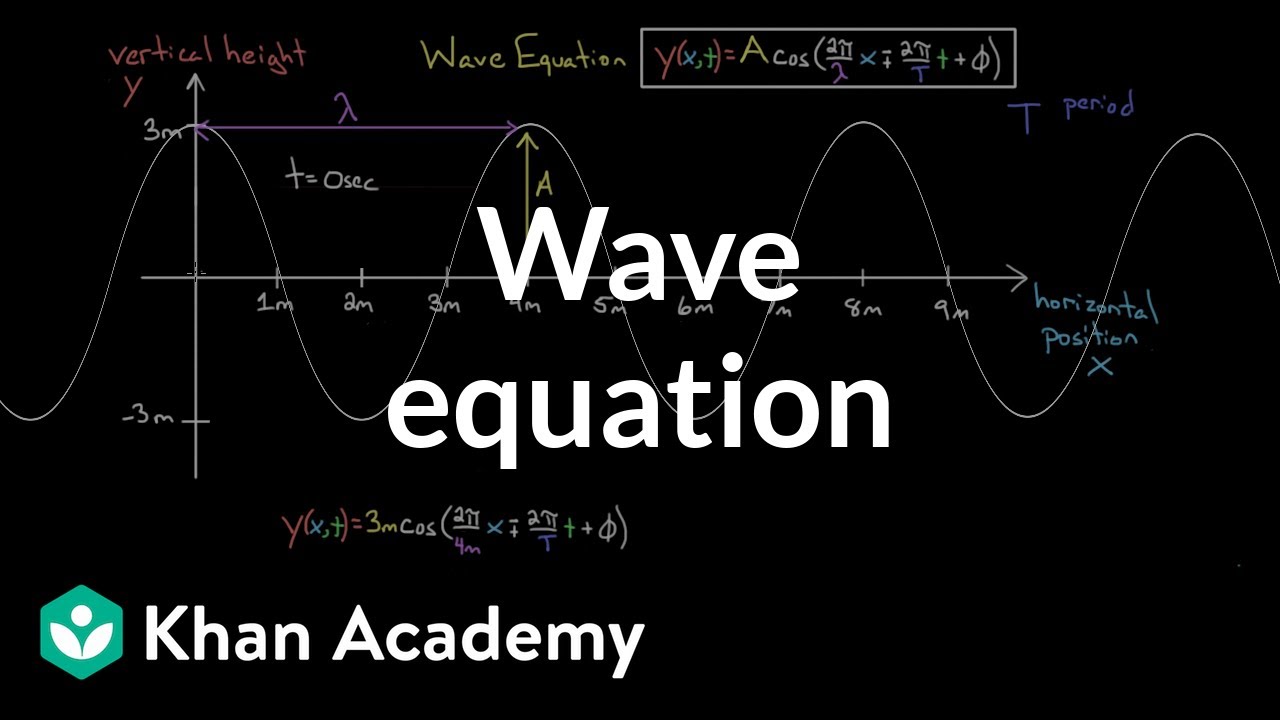
The equation of a wave | Physics | Khan Academy

30-60-90 Triangles - Special Right Triangle Trigonometry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Cosine WaveTrigonometrySine WaveComplementary AnglesRight TrianglesAmplitudePhase PlotGiant Wheel AnalogyMath EducationLearnabilityEducational Video