Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 4)
TLDRThe video transcript outlines a comprehensive AP Calculus practice session focusing on polar parametric vector problems. The instructor addresses multiple-choice questions from Unit 9 of Calc BC, covering topics such as calculating the distance between two points based on velocity and position, deriving the second derivative of 'y' with respect to 'x', and determining the speed of an object given its parametric equations. The session also delves into arc length calculations for parametric equations and explores finding the area enclosed by polar curves. The instructor emphasizes the importance of memorizing key formulas for success on the AP exam. The video is part of a larger series, with the presenter promising more parts to come, and concludes with a discussion on the tangent line to a parametric curve at a specific point, highlighting the need to understand calculus concepts and their application to novel problems.
Takeaways
- 📚 The video is focused on practicing multiple-choice questions for the AP Calculus exam, specifically unit nine of Calc BC, and is part four of an eight-part series.
- 🔢 The first problem discussed involves calculating the distance between two points on the path of a particle moving in the xy-plane, using the velocity function and the distance formula.
- ⏱️ The concept of the velocity and position of a particle at a given time is used to derive the position at time 't' and to calculate the distance traveled.
- 📐 The video covers the calculation of the second derivative of 'y' with respect to 'x', emphasizing the importance of memorizing key formulas for efficiency during exams.
- 🧮 The method of finding the speed of an object moving along a path in the xy-plane using parametric equations is explained, highlighting two different approaches to solving the problem.
- 📏 The arc length of a path described by parametric equations is calculated by integrating the magnitude of the velocity vector.
- 🔴 The total area enclosed by polar curves is found using the integral of the function describing the curve, with the interval determined by the bounds of the curve.
- 📈 The video explains how to find the acceleration vector of a particle in motion by taking the second derivative of the position function with respect to time.
- 🧵 The condition for a particle to be at rest is when both components of the velocity vector (dx/dt and dy/dt) are zero, and the video shows how to find the time 't' and the corresponding position where this occurs.
- 🔑 The value of a constant 'k' in a given parametric equation is determined by finding the slope of the tangent line at a specific point and using the given slope value.
- 📐 The slope of the tangent line to a polar curve at a particular point is found using both graphical insight and the formula for polar slope, demonstrating two methods to arrive at the solution.
- 📍 The equation of the tangent line to a curve defined by parametric equations at a specific point is determined by evaluating the derivatives at that point and using the point-slope form of a line.
Q & A
What is the main topic of the video?
-The video is focused on practicing multiple-choice questions related to polar parametric vector for the AP Calculus exam, specifically Unit 9 of Calc BC.
How does the video approach the calculation of the distance between two positions of a particle at different times?
-The video uses the distance formula, specifically the magnitude of the difference between the position vectors at the two times, and also demonstrates the use of the fundamental theorem of calculus to find the position at a later time by integrating the velocity function.
What is the significance of the second derivative of y with respect to x in the context of the video?
-The second derivative of y with respect to x is important for understanding how the rate of change of y with respect to x is itself changing, which is a key concept in calculus and is required to solve the problems presented in the video.
How does the video handle the calculation of the speed of an object moving along a path in the xy plane?
-The video calculates the speed by finding the magnitude of the velocity vector, which is the square root of the sum of the squares of the derivatives of x and y with respect to time.
What is the approach for finding the length of the path described by a parametric equation?
-The video uses the concept of arc length, which involves integrating the magnitude of the velocity (or speed) from one parameter value to another.
How does the video deal with the calculation of the area enclosed by a polar curve?
-The video discusses using the integral of the function representing the radial distance squared, multiplied by one-half, over the interval of interest to find the area enclosed by a polar curve.
What is the strategy for finding the total area of the region enclosed by two polar curves?
-The video suggests looking at the answer choices and using the symmetry and properties of the given polar curves to eliminate incorrect options and identify the correct one.
How does the video determine the acceleration vector of a particle in the xy plane?
-The video finds the acceleration vector by first determining the first and second derivatives of the position functions with respect to time and then forming the vector of these derivatives.
What is the criterion for a particle to be at rest in the context of the video?
-A particle is considered at rest if its velocity vector is zero, which means both the derivatives of the x and y position functions with respect to time are zero.
How does the video find the slope of the line tangent to a particle's path at a specific point?
-The video calculates the slope of the tangent line by finding the derivative of y with respect to x for the parametric equations of the particle's path and evaluating it at the given point in time.
What is the method used in the video to find the equation of the tangent line to a graph at a given point?
-The video uses the derivative of y with respect to x (slope of the tangent) and the coordinates of the given point to determine the equation of the tangent line.
Outlines
📚 AP Calculus BC Practice: Polar Parametric Vector
This video focuses on practicing multiple-choice questions for the AP Calculus BC exam, specifically from Unit 9. The presenter is working on a series of eight videos, with parts one to three already completed. The session begins with a detailed explanation of question 37, which involves calculating the distance between two points on the path of a particle moving in the xy-plane, given its velocity as a function of time. The presenter uses the distance formula and the fundamental theorem of calculus to find the position of the particle at two different times, t=1 and t=2, and then calculates the distance between these points. The explanation continues with a discussion of the second derivative of y with respect to x for parametric equations, emphasizing the importance of memorizing key formulas for success in the exam. The video also covers the calculation of speed for an object moving along a path in the xy-plane, given by parametric equations, and the length of the path described by another set of parametric equations.
🔍 Calculating Arc Length and Area with Parametric Equations
The presenter tackles the calculation of the length of a path described by parametric equations, emphasizing the use of the integral of the magnitude of velocity (speed) from one point to another. The video also addresses how to find the total area enclosed by a polar curve, using the integral of the function squared over the interval from 0 to π. The presenter discusses different methods for solving these problems, including using the rectangular graph to find polar areas and the importance of understanding the connections between rectangular and polar graphs. Additionally, the video covers how to determine the area enclosed by a polar curve with a loop, using the correct limits of integration and the relationship between the rectangular and polar graphs to find the inner loop of the curve.
📐 Analyzing Particle Motion and Rest States in Parametric Equations
The video script discusses the concept of a particle being at rest in the context of parametric equations, which means that the velocity vector is zero. The presenter solves a problem to find the point at which a particle's velocity is zero by setting the derivatives of the parametric equations equal to zero and solving for the parameter t. The video also explores another problem where the position of a particle is given by parametric equations involving natural logarithms, and the problem requires finding the value of a constant k such that the slope of the tangent line at a specific point is 8. The presenter demonstrates how to find the derivatives needed to calculate the slope and how to evaluate them at the given point to find the value of k.
📉 Calculating Tangent Slopes and Acceleration Vectors
The presenter addresses the calculation of the slope of the tangent line to a polar curve at a specific point where theta equals π. Two methods are discussed: one involves graphing the polar curve and identifying the slope by inspection, and the other involves using the formula for polar slope, which requires finding the derivatives with respect to θ and evaluating them at the given point. The video also covers the calculation of the acceleration vector of a particle in the xy-plane, given its position as a function of time. The acceleration vector is found by taking the second derivative of the position with respect to time. The presenter walks through the process of finding the derivatives and evaluates them to find the acceleration vector.
🧮 Solving for Tangent Lines and Particle Motion
The video concludes with a problem involving the calculation of the equation of the tangent line to a curve defined by parametric equations at a specific point. The presenter outlines the process of finding the derivatives of the parametric equations, evaluating them at the given point, and using them to determine the slope of the tangent line. The video highlights the importance of not confusing the variables and presents a strategy for solving such problems, including using the answer choices to guide the solution process. The presenter also emphasizes the value of practice, encouraging viewers to work through as many problems as possible to become familiar with the types of questions and solutions that may appear on the AP Calculus BC exam.
Mindmap
Keywords
💡Polar Parametric Vector
💡AP Calculus Exam
💡Velocity Vector
💡Distance Formula
💡Second Derivative
💡Parametric Equations
💡Arc Length
💡Polar Curve
💡Acceleration Vector
💡Tangent Line
💡Natural Logarithm
Highlights
The video provides practice for polar parametric vector multiple choice questions for the AP Calculus exam, covering Unit 9 of Calc BC.
The presenter plans to create a total of 8 parts, with this being Part 4.
Question 37 involves using the distance formula and fundamental theorem of calculus to find the distance between two points on the path of a moving particle.
Two different methods are demonstrated for solving Question 37 - using a calculator to find the integral, and finding the x and y coordinates separately.
For Question 38, the presenter emphasizes the importance of memorizing the formula for the second derivative of y with respect to x.
The second derivative of y with respect to x is derived by taking the derivative of dy/dx with respect to t.
Question 39 involves finding the speed of an object given its parametric equations, using the magnitude of the velocity vector.
The length of the path described by a particle is found using the integral of the magnitude of velocity from the start to end points.
For finding the area enclosed by a polar curve, the presenter recommends using the rectangular graph to identify the relevant interval and function to integrate.
The area enclosed by two polar curves is found by integrating the difference of their squared functions over the appropriate interval.
To find the acceleration vector of a particle, take the second derivative of its parametric equations for x and y.
A particle is at rest when its velocity vector (dx/dt and dy/dt) is equal to zero at a given point in time.
The slope of the tangent line to a parametric curve at a point can be found by evaluating dy/dx at that point.
For a polar curve, the slope of the tangent line at a point can be found using the derivatives dx/dθ and dy/dθ.
The equation of the tangent line to a parametric curve at a point is given by dy/dx = (dy/dt) / (dx/dt).
If the slope of the tangent line is undefined, the equation is simply x = the x-coordinate of the point of tangency.
The video provides a total of 48 practice problems covering a wide range of polar parametric vector topics.
Transcripts
Browse More Related Video

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 1)

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 2)

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 3)

1 | MCQ | Practice Sessions | AP Calculus BC

AP Calculus BC - 10 Minute Recap
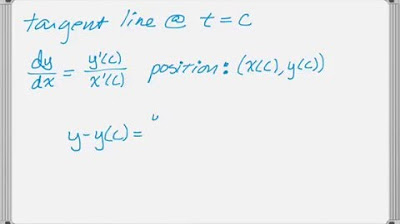
AP Calculus BC Parametric and Vector AP Exam Review
5.0 / 5 (0 votes)
Thanks for rating: