Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 2)

turksvids

24 Apr 202221:49

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is a comprehensive guide for AP Calculus BC exam preparation, focusing on multiple-choice questions involving polar parametric equations, vectors, and calculus concepts. The speaker discusses various problems, emphasizing the importance of understanding the fundamental theorem of calculus, velocity, and acceleration. Key topics include finding the position vector of a particle, calculating the second derivative with respect to x, determining the speed of an object, and computing the perimeter of an ellipse using parametric equations. The script also covers polar curve areas, instantaneous rate of change, and the equation of a tangent line to a parametric curve. The speaker uses a mix of algebraic manipulation and calculator work to solve the problems, providing insights into common pitfalls and tips for tackling similar questions on the exam.

Takeaways

📚 The video is part of a series focusing on practicing AP Calculus BC exam questions, specifically polar parametric and vector multiple choice questions.
⏱️ The instructor plans to cover four sets of questions before the exam and acknowledges the time-consuming nature of creating the video content.
🔁 It's suggested that viewers watch the previous videos for foundational knowledge, as the explanations in subsequent videos may become more concise.
🧮 The video uses the fundamental theorem of calculus to solve for the position vector of a particle moving in the x-y plane, given parametric equations.
📈 The process involves integrating dx/dt and dy/dt from a specific time 't' to find the position vector components x(t) and y(t).
🤔 The instructor emphasizes the importance of understanding the problem and the correct application of calculus formulas, especially when dealing with second derivatives.
📐 For tangent line problems, the video demonstrates how to find the derivative dy/dx by dividing dy/dt by dx/dt, and then using this to write the equation of the tangent line.
🔢 The video covers several problems, including finding the second derivative of y with respect to x, calculating the speed and acceleration of a particle, and determining the area bounded by polar curves.
📊 The area under curves is calculated using integrals, and the importance of correctly identifying the limits of integration and the functions to integrate is highlighted.
🧷 The video stresses the need for accuracy and attention to detail, especially when differentiating between position, velocity, and acceleration vectors.
⚙️ The use of a calculator is mentioned for certain problems, indicating that some questions require numerical methods for their solution.
📝 The instructor advises students to carefully read the problem statements to avoid mistakes, such as confusing the given velocity vector for a position vector.

Q & A

What is the main topic of the video?
-The video is about practicing polar parametric and vector multiple choice questions for the AP Calculus BC exam.
What is the significance of the fundamental theorem of calculus in the video?
-The fundamental theorem of calculus is used to rearrange and integrate given parametric equations to find the position vector of a particle at a specific time.
How does the video approach the problem of finding the second derivative of y with respect to x?
-The video uses the formula for the second derivative of y with respect to x, which involves the derivative of dy/dx with respect to t, and emphasizes the importance of finding dy/dt first.
What is the key to solving the problem involving the speed of a particle moving in the xy plane?
-The key is to find the magnitude of the velocity vector, which is the square root of the sum of the squares of dx/dt and dy/dt.
How does the video handle the calculation of the perimeter of an ellipse defined parametrically?
-The video calculates the perimeter by integrating the square root of dx/dt squared plus dy/dt squared from 0 to 2π, which represents the arc length of the ellipse.
What is the challenge when calculating the area of a region between two polar curves?
-The challenge is determining which curve is the outer one and which is the inner one, as this affects the order in which their areas are subtracted to find the region's area.
How does the video approach the problem of finding the instantaneous rate of change of r with respect to theta in polar coordinates?
-The video uses the quotient rule to find the derivative dr/dtheta and emphasizes the importance of careful reading and understanding of the problem.
What is the method to find the equation of the tangent line to a parametric curve at a specific point?
-The method involves finding dy/dx by dividing dy/dt by dx/dt, then using the point at which the tangent line is to be found to determine the slope and write the equation of the tangent line.
How does the video handle the problem of finding the slope of the line tangent to a polar curve at a specific point?
-The video uses the relationship between dy/dtheta and dx/dtheta to find the slope of the tangent line and evaluates the derivatives at the given point.
What are the common pitfalls to avoid when solving calculus problems in the video?
-Common pitfalls include confusing x and t, forgetting to square r when calculating polar area, and not carefully reading the problem to understand what is being asked (e.g., position, velocity, or acceleration vector).
What is the advice given for students preparing for the AP Calculus BC exam?
-The advice includes watching all the video parts for a comprehensive understanding, practicing multiple problems, and carefully reading and following the instructions in each problem.

Outlines

00:00

📚 AP Calculus BC Exam Preparation: Polar Parametric and Vector Questions

This paragraph introduces the video's focus on practicing polar parametric and vector multiple-choice questions for the AP Calculus BC exam. The speaker mentions it's part two of eight and hints at covering four topics before the exam, with a lighter explanation as the series progresses. The video begins with an example problem involving finding the position vector of a particle given parametric equations and its velocity.

05:01

🧮 Derivatives and Second Derivatives in Calculus Problems

The second paragraph delves into the process of finding second derivatives with respect to x in given parametric equations. It emphasizes the importance of memorizing formulas and correctly applying the power rule. The speaker also addresses a trickier question involving the second derivative of y with respect to x, cautioning against common mistakes and providing the correct approach.

10:03

🚀 Calculator Problems: Speed, Perimeter, and Area in Parametric and Polar Equations

This segment covers calculator-based problems, starting with finding the speed of an object given its parametric equations. It then moves on to calculating the perimeter of an ellipse using arc length and integral calculus. The speaker also discusses the area bounded by two polar curves, emphasizing the importance of identifying which curve is outer and using the correct integral expression for the area.

15:05

🔍 Identifying Curves and Calculating Instantaneous Rate of Change

The fourth paragraph addresses the challenge of determining which of two given polar curves is farther from the origin. It then explains how to calculate the instantaneous rate of change of r with respect to theta for a given polar curve equation. The speaker also touches on the importance of understanding different calculus operations in polar coordinates.

20:05

📐 Tangent Lines and Acceleration Vectors in Parametric Equations

The final paragraph discusses how to find the equation of a tangent line to a parametric curve at a specific point, emphasizing the need to find dy/dx and the coordinates at that point. It also covers finding the acceleration vector of a particle given its velocity vector and the importance of showing the derivative calculation in free-response questions.

🧵 Tangent Slope and Final Problem Summary

The last paragraph focuses on calculating the slope of the line tangent to a particle's path given its velocity vector components. It also briefly mentions the process for the next problem, which involves finding the slope of a tangent to a polar curve, highlighting the need to understand the relationship between polar and parametric derivatives.

Mindmap

Keywords

💡Parametric equations

Parametric equations are mathematical equations that express the coordinates of a point on a curve as functions of a third variable, known as the parameter. In the video, they are used to define the position of a particle moving in the x-y plane, which is a key concept for the AP Calculus BC exam preparation.

💡Velocity vector

A velocity vector is a vector that specifies an object's speed and direction of motion. In the context of the video, the velocity vector is given as a function of time, and it is used to find the position vector of a particle at a specific time.

💡Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus is a central theorem that links the concept of differentiating and integrating functions. In the video, it is used to find the position vector by integrating the velocity vector over a time interval, which is a common technique in calculus.

💡Second derivative

The second derivative of a function is the derivative of the first derivative. It provides information about the concavity of a function and can be used to find the points of inflection. In the video, the second derivative is used to find the rate of change of the rate of change of a function, which is important for understanding the behavior of the function.

💡Arc length

Arc length is the distance between two points along a curve. In the video, the concept of arc length is used to calculate the perimeter of an ellipse defined parametrically, which is an application of integral calculus.

💡Polar coordinates

Polar coordinates are a two-dimensional coordinate system in which each point is determined by a distance from a reference point and an angle from a reference direction. The video discusses polar curves and how to find the area bounded by them, which is a specific application of polar coordinates in calculus.

💡Tangent line

A tangent line is a line that touches a curve at a single point and has the same slope as the curve at that point. In the video, the equation of the tangent line to a curve at a specific parameter value is derived, which is a common problem in calculus involving finding the slope of the curve at that point.

💡Acceleration vector

Acceleration vector is a vector that represents the rate of change of velocity with respect to time. In the context of the video, the acceleration vector is found by taking the derivative of the velocity vector, which is a concept used to understand the dynamics of moving particles.

💡Product rule

The product rule is a fundamental theorem in calculus for differentiating the product of two functions. It is used in the video when finding the derivatives of functions that are products of other functions, such as when calculating the slope of a tangent line.

💡Power rule

The power rule is a basic rule in calculus used to differentiate functions of the form f(x) = x^n, where n is a constant. In the video, the power rule is used to find derivatives of polynomial and trigonometric functions, which is a standard technique in calculus.

💡Integration by substitution

Integration by substitution is a method for integrating a function of a function by changing the variable to make the integral easier to compute. Although not explicitly mentioned in the script, the concept is implied when integrating complex expressions, such as those involving parametric equations.

Highlights

The video discusses practicing for the AP Calculus BC exam with a focus on polar parametric and vector multiple choice questions.

The presenter plans to cover four sets of questions before the exam, hinting at the time-consuming nature of the content.

A methodical approach to solving problems using the fundamental theorem of calculus is emphasized.

The importance of understanding the position vector and velocity vector in parametric equations is covered.

Integration is used to find the position vector at a given time, showcasing a blend of algebraic and calculus techniques.

The concept of the second derivative of y with respect to x is introduced, highlighting its calculation using derivatives.

A calculator question demonstrates how to find the speed of a particle given its parametric equations.

The video covers the calculation of the perimeter of an ellipse using arc length, a key concept in calculus.

The area between two polar curves is calculated, illustrating the use of integral calculus in polar coordinates.

The instantaneous rate of change of a polar curve with respect to theta is determined using differentiation.

The acceleration vector of a particle is found by differentiating the velocity vector, a fundamental concept in physics and calculus.

The equation of a tangent line to a parametric curve is derived, emphasizing the relationship between derivatives and slopes.

The slope of a line tangent to a polar curve is calculated, showcasing the interplay between polar and Cartesian coordinates.

A comprehensive walkthrough of a calculator-based problem involving the velocity and position of a particle is provided.

The video concludes with a reminder to practice and review, underlining the importance of preparation for the AP Calculus BC exam.

Transcripts

Browse More Related Video

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 4)

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 1)

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 3)

2023 AP Calculus BC Free Response Question #2

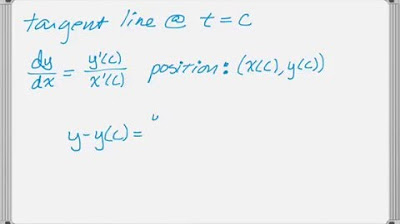
AP Calculus BC Parametric and Vector AP Exam Review

1 | MCQ | Practice Sessions | AP Calculus BC

Related Tags

AP Calculus Parametric Equations Vector Calculus Multiple Choice Exam Preparation Theoretical Math Educational Content Integral Calculus Derivatives Math Tutorial