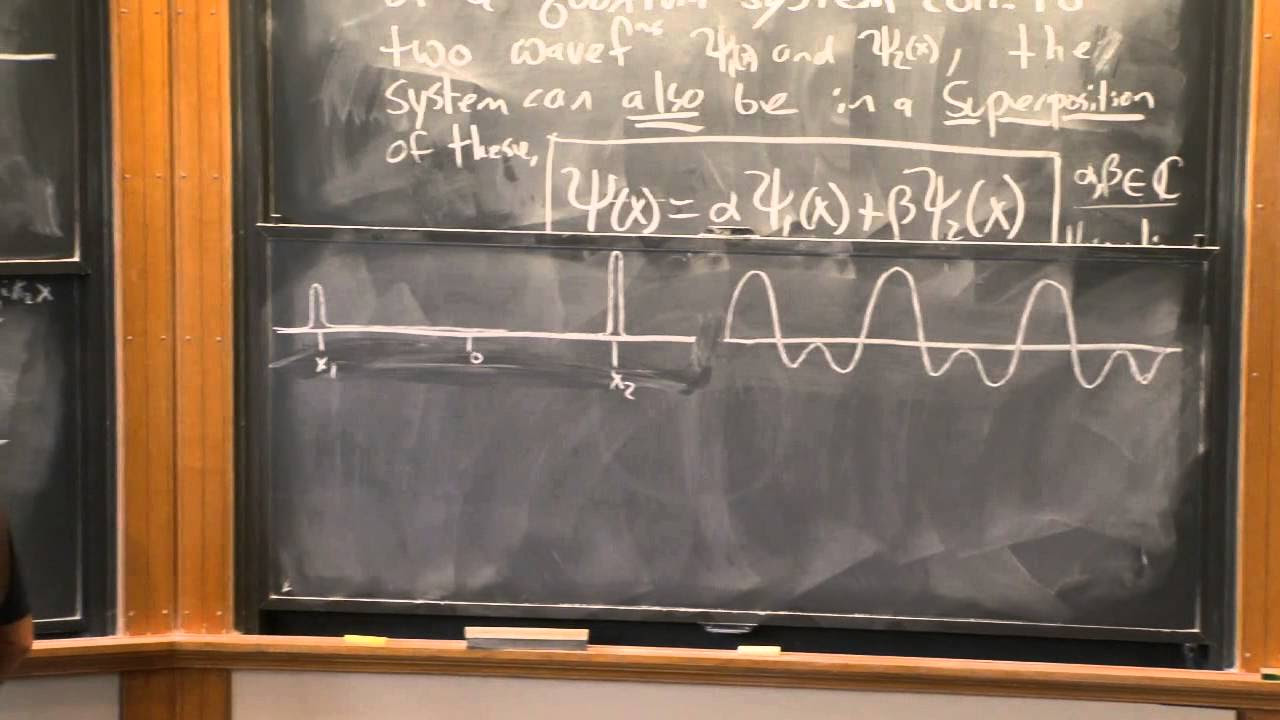Application: Quantum mechanics on curved spaces - Lec 26 - Frederic Schuller

Frederic Schuller

21 Sept 201592:15

EducationalLearning

32 Likes 10 Comments

TLDRThe transcript details a deep dive into quantum mechanics on curved space, challenging the traditional view of wave functions as complex-valued functions on physical space. The lecturer proposes a shift from the standard model to consider wave functions as sections of a vector bundle, leading to a more geometric interpretation. This approach allows for the definition of self-adjoint operators and the commutation relations essential for quantum mechanics, even in non-Cartesian coordinates and on curved spaces. The discussion involves intricate mathematical concepts such as covariant derivatives, the frame bundle, and the associated bundle, emphasizing the need to move beyond the conventional quantum mechanical framework to accommodate the complexities of curved spaces. The lecturer also touches on the implications for quantum gravity and the importance of understanding the geometric structure of quantum mechanics for a more profound comprehension of the subject.

Takeaways

📚 The course transitions from formal to informal, focusing on applications of quantum mechanics on curved space.
🌌 Quantum mechanics is typically introduced with wave functions in a position space representation, considering them as elements of an L2 space.
🚫 The traditional view of wave functions as complex-valued functions on physical space is challenged as untenable.
🔍 The need for self-adjoint operators acting on L2 space is discussed, but it's shown that they can't act in the expected way due to domain issues.
🧩 The Gelfand triple is introduced as a way to address issues of domains and targets for self-adjoint operators using Schwartz functions and tempered distributions.
📏 The script explores the implications of using non-Cartesian coordinates, such as polar coordinates, on the representation of quantum mechanical operators.
🤔 The concept of wave functions as sections of a vector bundle over physical space is proposed as a solution to the problem of operator domains and targets.
🔗 The importance of the frame bundle and connection on it is highlighted for understanding how quantum mechanics behaves under changes of coordinates.
⚙️ The covariant derivative is used to modify the definition of the momentum operator to make it suitable for curved spaces.
🧮 The script provides a detailed mathematical approach to ensure the commutation relations hold true in the context of curved spaces and non-Cartesian coordinates.
⛓ The transformation properties of the wave function and the Yang-Mills field under the frame bundle are discussed to understand the overarching structure of quantum mechanics on curved spaces.

Q & A

What is the main challenge when applying quantum mechanics to curved space?
-The main challenge is to define the wave function and the momentum operator in a way that is consistent with the commutation relations and self-adjointness properties, without being restricted to a particular choice of coordinates.
Why is the standard representation of the momentum operator problematic on curved space?
-The standard representation of the momentum operator as a partial derivative acting on a wave function leads to issues with self-adjointness and the domain of the operator when applied to non-Cartesian coordinates on a curved space.
What is the role of the Gelfand triple in addressing the issues with the domain and target of operators?
-The Gelfand triple provides a framework for embedding the space of square-integrable functions into a larger space of Schwartz functions and tempered distributions, which allows for a proper definition of self-adjoint operators and addresses issues related to the domain and target of these operators.
How does the concept of a vector bundle help in defining quantum mechanics on curved spaces?
-The concept of a vector bundle allows for the wave function to be considered as a section of a complex vector bundle over the curved space, which provides a more general and coordinate-independent framework for defining the wave function and the momentum operator.
What is the significance of the Yang-Mills field in the modified definition of the momentum operator?
-The Yang-Mills field represents the connection on the frame bundle associated with the vector bundle, and its inclusion in the modified definition of the momentum operator allows for the correct transformation properties under changes of coordinates and ensures the self-adjointness of the operator.
How does the script suggest modifying the standard definition of the momentum operator?
-The script suggests modifying the standard definition of the momentum operator by replacing the partial derivative with a covariant derivative, which includes an additional term involving the Yang-Mills field, thus making the operator consistent with the geometry of the curved space.
What is the importance of the metric tensor in defining an inner product on a curved space?
-The metric tensor provides the necessary information about the geometry of the curved space, and its determinant, when included in the integral, ensures that the inner product is invariant under changes of coordinates, which is crucial for defining quantum mechanics on curved spaces.
Why is it incorrect to consider the wave function as a complex-valued function on the physical space?
-Considering the wave function as a complex-valued function on the physical space leads to inconsistencies when dealing with non-Cartesian coordinates or curved spaces, as it does not account for the underlying geometry and the need for a more general framework that includes the concept of a vector bundle.
How does the script relate the mathematical concepts of differential geometry to quantum mechanics?
-The script relates differential geometry to quantum mechanics by using concepts such as vector bundles, connections, and covariant derivatives to provide a geometric framework for defining the wave function and the momentum operator in a way that is consistent with the geometry of the space, whether it is flat or curved.
What is the purpose of introducing the frame bundle in the context of quantum mechanics on curved spaces?
-The frame bundle is introduced to provide a way to define a connection and a covariant derivative on the associated vector bundles, which is essential for defining the momentum operator in a coordinate-independent way and for understanding how quantum mechanics behaves under changes of coordinates on a curved space.
How does the script address the issue of the wave function's transformation properties under changes of coordinates?
-The script addresses this issue by proposing that the wave function should be considered as a section of a complex vector bundle, which transforms appropriately under changes of coordinates, rather than a simple complex-valued function on the physical space, thus providing a more general and consistent framework for quantum mechanics on curved spaces.

Outlines

00:00

📘 Introduction to Quantum Mechanics on Curved Space

The speaker begins by transitioning from formal to informal discussion, focusing on quantum mechanics within curved space. The traditional approach to quantum mechanics, involving wave functions and operators on L2 spaces, is critiqued for its limitations. The need to recognize structures beyond the standard model is emphasized, paving the way for a deeper exploration into the subject.

05:02

🧬 Self-Adjoint Operators and Commutation Relations

The paragraph delves into the properties of self-adjoint operators and their role in quantum mechanics. The speaker challenges the standard representation of quantum operators in position space, highlighting issues with the domain and range of these operators. The use of the Gelfand triple is introduced as a method to address these issues, embedding the space of square-integrable functions into a larger dual space.

10:04

🚫 Critique of Wave Function as a Complex-Valued Function

The paragraph addresses the misconception that wave functions are simply complex-valued functions on physical space. The speaker argues that this perspective is flawed and leads to incorrect assumptions about quantization rules and the representation of operators. The need to abandon this idea and consider wave functions in a different light is stressed.

15:05

🔄 Coordinate Invariance and the Frame Bundle

The speaker emphasizes the importance of not being restricted to a particular choice of coordinates, which is a common pitfall in quantum mechanics. The concept of using polar coordinates instead of Cartesian ones is explored, and the challenges that arise when attempting to maintain commutation relations and self-adjointness for operators under such transformations are discussed.

20:06

🎢 Generalized Inner Product and Metric Manifolds

The paragraph introduces the concept of a metric manifold, where the base space is equipped with a zero-two tensor field, or a metric. The speaker discusses how the determinant of this metric can be used to define an inner product that is invariant under changes of coordinates. This approach allows for a more general formulation of quantum mechanics on curved spaces.

25:07

🛠 Modification of Momentum Operator and Covariant Derivatives

The speaker proposes a modification to the definition of the momentum operator by incorporating covariant derivatives. This modification is necessary to account for the extra terms that arise when considering wave functions as sections of a line bundle. The use of covariant derivatives allows for the inclusion of connection terms, which are essential for maintaining the commutation relations in curved spaces.

30:17

🔗 Bundles and Connection Forms in Quantum Mechanics

The paragraph discusses the geometric interpretation of wave functions and operators in the context of bundles and connection forms. The speaker suggests that wave functions can be considered as sections of a complex line bundle associated with the frame bundle of the space. This geometric perspective allows for a more coherent understanding of quantum mechanics on curved spaces and the role of the Yang-Mills fields.

35:20

🌐 Quantum Mechanics on Curved Spaces: The Bigger Picture

The speaker concludes by emphasizing the need to rethink the concept of wave functions in quantum mechanics, especially when dealing with curved spaces. The traditional view of wave functions as complex-valued functions on physical space is challenged, and the importance of understanding the underlying geometric structures, such as bundles and connection forms, is highlighted. The aim is to reconcile these geometric concepts with the known principles of quantum mechanics.

Mindmap

Keywords

💡Quantum Mechanics

Quantum mechanics is a fundamental theory in physics that describes how the physical world operates at the smallest scales, typically at the level of atoms and subatomic particles. In the video, it is discussed in the context of its application on curved space, which is a departure from the standard approach that assumes a flat space-time. The exploration of quantum mechanics on a curved background is essential for understanding phenomena in the presence of gravity or for developing a theory of quantum gravity.

💡Wave Function

A wave function, often denoted by the Greek letter psi (Ψ), is a mathematical description of the quantum state of a particle or system of particles. It is a core concept in quantum mechanics. The video challenges the traditional view of the wave function as a complex-valued function on physical space, suggesting that this perspective may be untenable in the context of curved spaces.

💡Self-Adjoint Operators

In the context of the video, self-adjoint operators are essential in quantum mechanics as they are associated with observable quantities. The script discusses the need for operators like position (Q) and momentum (P) to be self-adjoint with respect to an inner product, which is a requirement for these operators to correspond to measurable physical quantities. The issue of self-adjointness arises when considering non-Cartesian coordinates or curved spaces.

💡Commutation Relations

Commutation relations are mathematical expressions that describe the behavior of operators under the operation of commutation, which is the order in which operations are performed. In quantum mechanics, the commutation relations between position and momentum operators are crucial as they lead to the Heisenberg uncertainty principle. The video explores these relations in the context of different coordinate systems and curved spaces.

💡Covariant Derivative

The covariant derivative is a concept from differential geometry that generalizes the notion of a derivative to curved spaces. It is used in the video to redefine the momentum operator in a way that is consistent with the geometry of the space. This is important because the standard partial derivative does not account for the curvature of space, which is necessary when considering quantum mechanics on a curved manifold.

💡Curvature of Space

The curvature of space is a concept from general relativity that describes how space is bent by mass and energy. In the video, the curvature of space is central to the discussion of how quantum mechanics can be formulated on spaces that are not flat. Understanding quantum mechanics in curved spaces is important for applications in cosmology and the study of black holes.

💡Gelfand Triple

A Gelfand triple is a mathematical construct that relates different function spaces, often used in the context of quantum mechanics to deal with issues of domains and ranges of operators. In the script, the Gelfand triple is mentioned as a way to address the problem of domains and targets for self-adjoint operators, which is crucial for defining quantum observables.

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system in which each point is determined by a radius and an angle from a reference point. The video uses polar coordinates as an example to illustrate the challenges of defining quantum mechanical operators in non-Cartesian systems. The transition from Cartesian to polar coordinates highlights the need for a more general framework for quantum mechanics on curved spaces.

💡Vector Bundle

A vector bundle is a topological space that locally resembles a product space, but globally may have a different topological structure. In the context of the video, the idea of a vector bundle is used to reconceptualize the wave function not as a function on physical space, but as a section of a complex vector bundle over the space. This perspective helps to resolve issues related to the definition of quantum mechanical operators on curved spaces.

💡Yang-Mills Field

The Yang-Mills field is a mathematical concept used in physics to describe the gauge fields that mediate the strong and weak nuclear forces. In the video, the Yang-Mills field is discussed in the context of modifying the definition of the momentum operator to account for the curvature of space. The field is used to define an additional term in the covariant derivative acting on sections of a bundle.

💡Metric Manifold

A metric manifold is a smooth manifold equipped with a metric tensor, which defines a notion of distance on the manifold. The concept is central to the generalization of quantum mechanics to curved spaces. The video discusses the use of the metric tensor to define an inner product on the manifold, which is essential for formulating quantum mechanics in a way that is independent of the choice of coordinates.

Highlights

Introduction of quantum mechanics on curved space, emphasizing a shift from traditional formalism to a more exploratory approach.

Discussion on the limitations of representing wave functions as elements of L2 space over a real, D-dimensional space.

The subtleties of defining self-adjoint operators in the context of quantum mechanics and their action on L2 space.

Challenges with the traditional representation of the momentum operator and the need for a domain larger than square-integrable functions.

Introduction of the Gelfand triple as a tool to address issues related to domains and targets of self-adjoint operators.

The concept of wave functions as sections of a C-vector bundle over Rd, providing a new perspective on quantum mechanics.

The use of covariant derivatives as a means to generalize the momentum operator for use on curved spaces.

Exploration of the properties of the inner product in the context of a general metric manifold, crucial for quantum mechanics on curved spaces.

Derivation of the commutation relations for position and momentum operators in a more general coordinate system.

The importance of the determinant of the metric tensor in defining integrals over a manifold for quantum mechanics.

The revelation that the wave function is not a function on physical space, contradicting a common assumption in quantum mechanics.

Proposal to consider the wave function as a section of a vector bundle associated with the frame bundle of the manifold.

The need to redefine the momentum operator to account for the curvature of space, leading to the introduction of the Yang-Mills field.

Investigation into how the choice of coordinates affects the self-adjointness of operators in quantum mechanics.

The realization that the wave function should be understood as a section of a complex line bundle, not just a complex-valued function.

The application of these concepts to understand quantum mechanics on a sphere, a common problem in quantum physics.

Final remarks on the necessity to move beyond traditional quantum mechanics formalism to understand quantum mechanics on curved spaces.

Transcripts

Browse More Related Video

Covariant derivatives - Lec 25 - Frederic Schuller

Lecture 6 | Quantum Entanglements, Part 1 (Stanford)

Lecture 3: The Wave Function

Parallel transport - Lec 23 - Frederic Schuller

Advanced Quantum Mechanics Lecture 3

Advanced Quantum Mechanics Lecture 6

Related Tags

Quantum Mechanics Curved Space Wave Function Covariant Derivative Geometric Framework Self-Adjoint Operators Polar Coordinates Functional Analysis Differential Geometry Vector Bundles Young-Mills Field