2010 AP Calculus AB Free Response #1

Allen Tsao The STEM Coach
28 Oct 201809:31
EducationalLearning
32 Likes 10 Comments

TLDRAllen from Bottle Stem Coach begins a video tutorial on AP Calculus AB 2010 response questions. He emphasizes the importance of using a graphing calculator for the exam and sets it up for easy access. The video focuses on a rate question involving the accumulation of snow on a driveway from midnight to 6 a.m., with the snowfall rate given by a function of time. Janet starts removing the snow at 6 a.m., and her rate of removal is also provided. The video walks through the process of calculating the amount of snow accumulated by 6 a.m., the rate of change in the volume of snow at 8 a.m., and the total amount of snow removed from the driveway at different times using integral calculus. Allen explains how to represent the total amount of snow removed as a piecewise function and how to calculate the amount of snow in the driveway at 9 a.m. The video concludes with a review of the calculations and a reminder to engage with the content through comments, likes, or subscriptions.

Takeaways
  • 📚 The video is a tutorial on AP Calculus AB 2010 response questions.
  • 🧮 A graphing calculator is necessary for solving the problems presented.
  • ❄️ The problem involves calculating the accumulation of snow on a driveway over time.
  • 🕒 The rate of snow accumulation and removal is given in cubic feet per hour.
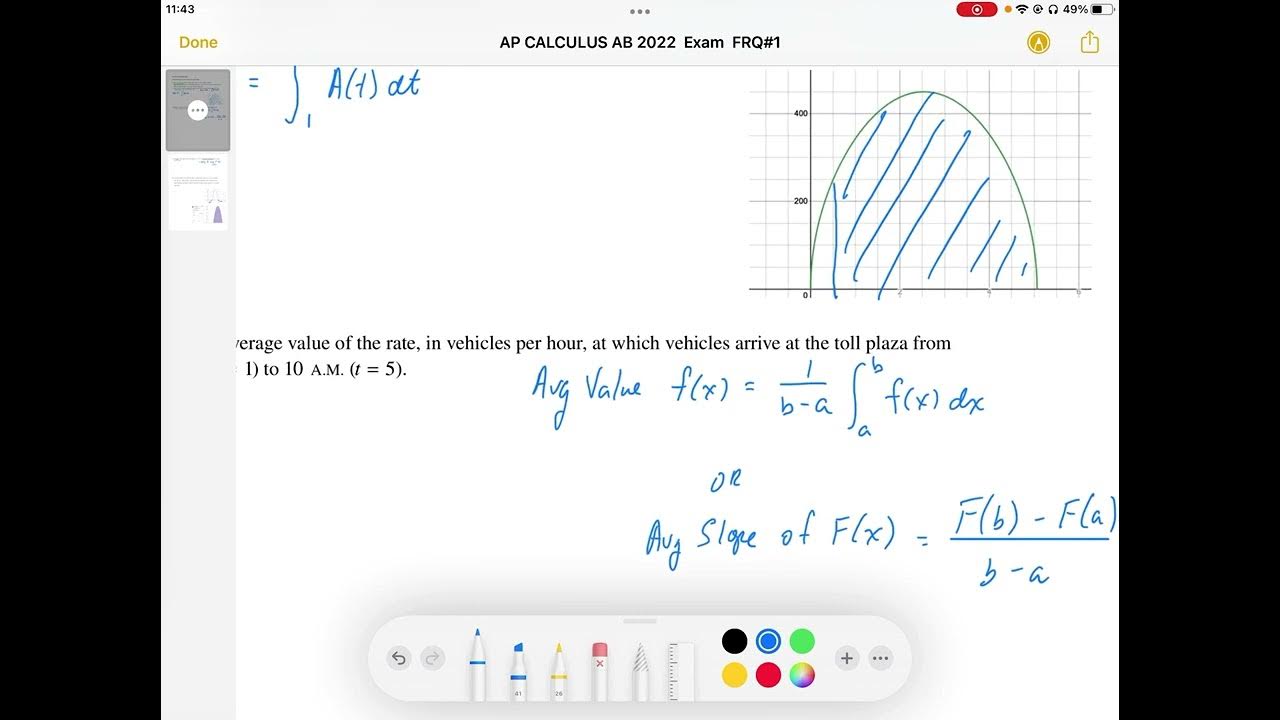
  • 🔍 The first step involves integrating the rate of snow accumulation from midnight to 6 a.m.
  • 📉 The rate of change in the volume of snow on the driveway at 8 a.m. is calculated by subtracting the removal rate from the accumulation rate.
  • 🤔 The piecewise function H(T) represents the total amount of snow removed from the driveway by time T hours since midnight.
  • 📈 H(T) is defined for different intervals: 0 to 6 a.m., 6 a.m. to 7 a.m., and 7 a.m. to 9 a.m.
  • 🧱 The final part of the problem calculates the total amount of snow in the driveway at 9 a.m. by integrating the rate of accumulation minus the rate of removal from 0 to 9 hours.
  • 📝 The presenter emphasizes the importance of setting up the integral correctly and checking the solution against the provided answer.
  • 💡 The video concludes with an invitation for viewers to engage with the content through comments, likes, or subscriptions, and offers additional help on twitch and discord.
Q & A

  • What is the purpose of Allen setting up a graphing calculator in the video?

    -Allen sets up a graphing calculator to solve calculus problems, specifically to compute integrals and evaluate functions, which are essential for addressing the AP Calculus AB free response questions he is working through.

  • Why does Jana start removing snow at 6 a.m. in the problem discussed?

    -Jana starts removing snow at 6 a.m. because this is the time she wakes up and begins the task of clearing her driveway, as indicated by the problem scenario where her snow removal rate is zero before this time.

  • What is the integral calculation Allen performs for the period from midnight to 6 a.m.?

    -Allen calculates the integral of the snow accumulation rate, modeled by the function 7t e^cos(t) from 0 to 6, to find out how much snow has accumulated by 6 a.m.

  • What does the function G(t) represent in the problem?

    -The function G(t) represents the rate at which Jana removes snow from her driveway, measured in cubic feet per hour.

  • How does Allen determine the rate of change in the volume of snow at 8 a.m.?

    -Allen determines the rate of change in the volume of snow at 8 a.m. by subtracting the snow removal rate G(t) from the snow accumulation rate F(t) at t = 8 hours.

  • What is the significance of the piecewise function H(t) that Allen discusses?

    -The piecewise function H(t) represents the total amount of snow Jana has removed from her driveway over time. It's defined based on different intervals reflecting the changing rates of snow removal as the day progresses.

  • Why did Allen need to correct his graphing calculator input?

    -Allen needed to correct his input because the graphing calculator did not initially recognize his function due to a syntax error in the multiplication expression, indicating the importance of correct syntax when using mathematical tools.

  • What method does Allen use to compute the amount of snow in the driveway by 9 a.m.?

    -Allen computes the total snow by 9 a.m. by calculating the integral of the net snow accumulation (F(t) - G(t)) from 0 to 9 hours.

  • What does Allen imply by mentioning cubic feet per hour in the context of rate of change?

    -Allen mentions cubic feet per hour to clarify that the rate of change he calculated (for snow being removed or accumulated) is in terms of volume change per unit of time, which aligns with the units of the functions F(t) and G(t).

  • What additional resources does Allen offer at the end of the video?

    -At the end of the video, Allen mentions that he offers free homework help on platforms like Twitch and Discord, inviting viewers to follow his content and join his community for additional support.

Outlines
00:00
📚 AP Calculus AB 2010 Response Questions Overview

Allen introduces the AP Calculus AB 2010 response questions and emphasizes the need for a graphing calculator. He discusses the accumulation of snow on a driveway from 9:00 a.m., using a rate function involving cosine. Allen then calculates the amount of snow accumulated by 6:00 a.m. and the rate of change at 8:00 a.m., noting the removal of snow by Janis. The summary includes the use of integrals and derivatives to solve the problems, as well as the setup of a piecewise function to represent the total amount of snow removed by a certain time.

05:04
🧮 Calculating Snow Accumulation and Removal

Allen continues to work through the calculus problem, focusing on the piecewise function H(T) that represents the total amount of snow removed from the driveway by time T hours since midnight. He explains the process of setting up the function based on the rate of snow removal and the time intervals. The summary includes the calculation of the integral from 0 to 9 of the rate of accumulation minus the rate of removal, leading to the final amount of snow on the driveway at 9:00 a.m. The video concludes with a review of the solution and an invitation for viewers to engage with the content and seek further help on platforms like Twitch and Discord.

Mindmap
Keywords
💡AP Calculus
AP Calculus refers to the Advanced Placement Calculus course and exam offered by the College Board. In the video, it is the subject matter that the speaker is addressing, specifically the 2010 response questions. The theme of the video revolves around solving calculus problems, which are part of the AP Calculus curriculum.
💡Graphing Calculator
A graphing calculator is a type of electronic device that is capable of plotting graphs of functions and solving complex mathematical problems. In the context of the video, the speaker mentions setting up a graphing calculator because it is an essential tool for solving calculus problems, such as integration and differentiation, which are discussed throughout the video.
💡Integral
In calculus, an integral represents the area under a curve defined by a function. The speaker uses integration to calculate the accumulation of snow on a driveway, which is a key part of the problem-solving process in the video. The integral is a fundamental concept in calculus and is central to the video's theme of solving AP Calculus problems.
💡Rate
The term 'rate' in the context of the video refers to the rate at which snow accumulates or is removed from a driveway, measured in cubic feet per hour. The concept of rate is integral to the problem, as it helps determine the volume of snow over time. The video discusses both the accumulation rate of snowfall and the removal rate by the character Janis.
💡Piecewise Defined Function
A piecewise defined function is a mathematical function that is defined by multiple sub-functions, each applicable to a different interval or 'piece' of its domain. In the video, the speaker uses a piecewise function to represent the total amount of snow removed from the driveway at different times throughout the day, which illustrates the changing rates of snow removal.
💡Domain
In mathematics, the domain of a function refers to the set of all possible input values (or 'T' in the video's context) for which the function is defined. The speaker specifies the domain of the function H of T as 'zero to T hours', which means the function applies to the time period starting from midnight up to the current hour T.
💡Rate of Change
The rate of change, also known as the derivative in calculus, measures how a quantity changes with respect to another quantity. In the video, the speaker calculates the rate of change in the volume of snow on the driveway at 8 a.m., which is determined by the difference between the accumulation rate and the removal rate at that specific time.
💡Cubic Feet
Cubic feet is a unit of volume used to express the amount of space a substance occupies. In the video, the speaker uses cubic feet to measure the volume of snow that accumulates on the driveway and the volume that is removed. It is a key unit for the mathematical calculations and integral to the problem's solution.
💡Midnight
In the video, midnight serves as the starting point (or 'T=0') for measuring time in hours since the snow began to fall. It is the reference point for the calculations of snow accumulation and removal rates throughout the day, as the problem unfolds over a period starting from midnight.
💡Snow Accumulation
Snow accumulation refers to the build-up of snow over time, which is a central scenario in the video's mathematical problem. The speaker calculates the amount of snow that accumulates on the driveway from midnight to various times during the day, using calculus to model and solve the problem.
💡Derivative
The derivative in calculus is a measure of the rate at which a function is changing at a given point. In the context of the video, the speaker uses the concept of the derivative to find the rate of change in the volume of snow on the driveway, which is a critical step in solving the calculus problem presented.
Highlights

Starting AP Calculus AB 2010 response questions

Importance of setting up a graphing calculator for the exam

Snow accumulation rate on Janet's driveway modeled by a function of time

Janet starts removing snow at 6:00 a.m. with a given rate function

Calculation of snow accumulation by 6 a.m. using integration

Use of a graphing calculator to solve the integral

The rate of change in the volume of snow at 8 a.m. is calculated

Snow is being removed at a specific rate, indicated by the difference between accumulation and removal rates

Defining H(t) as the total amount of snow removed from the driveway at time T

Expression of H(t) as a piecewise function based on the time of day

Integration used to find the amount of snow on the driveway at 9:00 a.m.

Subtracting the integral of the removal rate from the accumulation rate

Final calculation of snow on the driveway using a calculator

Verification of the result against the provided answer

Explanation of the piecewise function for H(t) and its boundary conditions

Offering free homework help on twitch and discord

Invitation for viewers to comment, like, or subscribe for more content

Transcripts

Browse More Related Video

AP CALCULUS AB 2022 Exam Full Solution FRQ#1(a,b)

2022 AP Calculus AB BC Free Response #1

2016 AP Calculus AB Free Response #1

2013 AP Calculus AB Free Response #1

2013 AP Calculus AB Free Response #3

2008 AP Calculus AB Free Response #3

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusGraphing CalculatorSnow AccumulationRate QuestionsIntegral CalculusExam PreparationAllen's TutorialEducational ContentMath Problem SolvingPiecewise FunctionsDriveway Scenario