What is Cronbach's Alpha? - Explained Simply (Part 2)
TLDRThe transcript discusses Cronbach's Alpha, a measure of internal consistency reliability for composite scores derived from multiple items or indicators. It emphasizes that reliability is determined by the number of items and the average correlation between them. The formula for Cronbach's Alpha is presented as a ratio of the number of items multiplied by the average inter-item correlation to the total variance in composite scores. An example is given with a 5-item scale, where the average correlation is 0.3, resulting in a reliability estimate of 0.73, indicating that 73% of the variance in the composite score is reliable. The transcript also highlights the impact of the number of items on reliability, noting that a higher number of items can lead to higher reliability even with lower average correlations. This insight is crucial for those designing scales for psychological or behavioral assessments.
Takeaways
- 📊 **Composite Scores Focus**: The discussion is centered around composite scores, which are the sum of individual item scores, rather than the individual item scores themselves.
- 🔍 **Internal Consistency Reliability**: Cronbach's alpha is used to measure how reliable these composite scores are, focusing on the average correlation between items.
- 📌 **Formula Insight**: The formula for Cronbach's alpha is presented as a ratio of the number of items multiplied by the average inter-item correlation to the total variance in composite scores.
- 📈 **Impact of Item Count**: The number of items in a scale has a significant positive nonlinear effect on the reliability estimate, with a rapid increase in reliability as the number of items increases.
- 🔢 **Example Calculation**: An example is provided to illustrate how to calculate Cronbach's alpha using a 5-item scale with positive, small to moderate correlations between items.
- 📉 **Average Correlation Effect**: Even with a low average inter-item correlation, a higher number of items can still result in a high reliability estimate, as demonstrated with a hypothetical 60-item scale.
- 🔧 **Standardization Note**: Cronbach's alpha can be calculated using standardized data (correlations) or unstandardized data (covariances), but the standardized approach is considered more intuitive.
- 📚 **Behavioral Science Context**: The script mentions that the typical correlation matrix for a 5-item scale in behavioral sciences would have positive, small to moderate correlations.
- 🔮 **Reliability Estimation**: The example shows how to estimate the reliability associated with composite scores, indicating that a certain percentage of the variance in the composite score is reliable.
- ⚖️ **Ratio of Variances**: Cronbach's alpha is described as the ratio of true score variance to total variance, providing insight into the proportion of reliable variance in the scores.
- 📘 **Scale Construction Considerations**: The importance of considering the number of items when constructing a scale is emphasized, as it greatly influences the internal consistency reliability.
Q & A
What are composite scores in the context of the transcript?
-Composite scores refer to the total scores for each person calculated by summing their individual scores across multiple items in a test or assessment.
What is internal consistency reliability?
-Internal consistency reliability is a measure of how well a set of items or indicators (such as test questions) measures a single unidimensional latent construct. It assesses the extent to which all items in a test contribute equally to the overall score.
What is Cronbach's Alpha and how is it calculated?
-Cronbach's Alpha is a statistic used to measure the reliability of a set of items as a single scale. It is calculated as the ratio of the mean inter-item correlation to the total variance of the composite scores, standardized by multiplying by the number of items.
What does the numerator in Cronbach's Alpha formula represent?
-The numerator in Cronbach's Alpha formula is the product of the number of items (K) and the mean of the inter-item correlations (R bar), which represents the average correlation between the items.
What is the denominator in Cronbach's Alpha formula?
-The denominator in Cronbach's Alpha formula is the total variance associated with the composite scores, which represents the overall variability in the scores across all items.
Why is the number of items important in calculating Cronbach's Alpha?
-The number of items is important because it has a positive nonlinear effect on the reliability estimate. As the number of items increases, the internal consistency reliability tends to increase, especially when moving from a smaller to a larger number of items.
What is the significance of the average inter-item correlation in Cronbach's Alpha?
-The average inter-item correlation (R bar) is significant because it indicates the degree to which each item is related to every other item in the scale. Higher average correlations generally lead to higher reliability estimates, assuming a sufficient number of items.
How does the size of the correlations between items affect Cronbach's Alpha?
-The size of the correlations between items affects Cronbach's Alpha in that larger correlations typically result in a higher reliability estimate. However, even with low average correlations, a large number of items can still yield a high reliability estimate.
What does it mean if a Cronbach's Alpha value is 0.73?
-A Cronbach's Alpha value of 0.73 indicates that 73% of the variance in the composite score is considered reliable variance, meaning that the items in the scale are generally consistent and measure the intended construct well.
What is the impact of having 60 items in a scale with an average inter-item correlation of 0.07 on Cronbach's Alpha?
-Even with a low average inter-item correlation of 0.07, having 60 items in a scale can result in a high Cronbach's Alpha value (e.g., 0.8), indicating that a large number of items can compensate for low correlations and still provide a reliable measure.
What is the typical correlation matrix you might get from a 5-item scale in the behavioral sciences?
-A typical correlation matrix from a 5-item scale in the behavioral sciences would have positive correlations between items, with magnitudes that are small to moderate, such as correlations of 0.35 between item 1 and item 2, and 0.42 between item 1 and item 3.
How does the concept of 'true score variance' relate to Cronbach's Alpha?
-In the context of Cronbach's Alpha, 'true score variance' refers to the portion of the total variance in the composite scores that is considered reliable and due to the underlying construct being measured. Cronbach's Alpha is essentially the ratio of true score variance to total variance.
Outlines
📊 Understanding Cronbach's Alpha for Internal Consistency Reliability
This paragraph explains the concept of internal consistency reliability using Cronbach's Alpha. It focuses on composite scores rather than individual item scores. The formula for Cronbach's Alpha is discussed, which is a ratio of the number of items multiplied by the average inter-item correlation, divided by the total variance in the composite scores. An example is provided using a 5-item scale with positive, small to moderate correlations between items. The reliability estimate is calculated to be 0.73, indicating that 73% of the variance in the composite score is reliable. The impact of the number of items in a scale on Cronbach's Alpha is also emphasized, with a nonlinear positive effect as the number of items increases.
🔢 Impact of Item Count on Cronbach's Alpha
This paragraph continues the discussion on Cronbach's Alpha by illustrating the impact of the number of items in a scale. An example is given comparing a 5-item scale with an average inter-item correlation of 0.3 to a 60-item scale with a much lower average correlation of 0.07. Despite the lower correlation, the Cronbach's Alpha estimate for the 60-item scale is higher at 0.82, demonstrating that 82% of the variance in the composite scores is reliable. This highlights the significant effect of the number of items on the reliability estimate, with a rapid increase in internal consistency reliability as the number of items increases from 2 to 10, followed by a steady increase.
Mindmap
Keywords
💡Composite scores
💡Internal consistency reliability
💡Cronbach's Alpha
💡Inter-item correlation
💡Standardized Cronbach's Alpha
💡True score variance
💡Total variance
💡Correlation matrix
💡Number of items
💡Behavioral sciences
💡Reliability estimate
Highlights
Composite scores are used to assess the internal consistency reliability of a test or scale.
Cronbach's alpha is a measure of how well a set of items or indicators measure a single unidimensional latent construct.
There are multiple formulas for calculating Cronbach's alpha, but the most accessible one is a ratio of true score variance to total variance.
The formula for Cronbach's alpha involves multiplying the number of items (K) by the mean inter-item correlation (r bar).
Internal consistency reliability can be applied to composite scores based on sums of items, subscales, or other positively correlated constructs.
Cronbach's alpha can be calculated using standardized data (correlations) or unstandardized data (covariances).
The numerator of the Cronbach's alpha formula is K times r bar, representing the average inter-item correlation.
The denominator is the total variance in the composite scores.
Cronbach's alpha estimates the proportion of reliable variance in the composite scores.
An example calculation of Cronbach's alpha for a 5-item scale with positive, small to moderate inter-item correlations is provided.
The average inter-item correlation for the 5-item scale is 0.3, resulting in a Cronbach's alpha of 0.73.
This means 73% of the variance in the composite scores is considered reliable variance.
The number of items in a scale has a positive nonlinear effect on the Cronbach's alpha estimate of internal consistency reliability.
As the number of items increases, there is a rapid increase in reliability from 2 to 10 items, followed by a steady increase from 11 onwards.
An example is given where a 60-item scale with a low average inter-item correlation of 0.07 still yields a high Cronbach's alpha of 0.8.
This demonstrates that even with low inter-item correlations, a large number of items can result in high reliability.
It is important to consider the number of items when estimating the reliability of a scale using Cronbach's alpha.
The impact of the number of items on Cronbach's alpha is significant and should not be overlooked.
Transcripts
Browse More Related Video

What is Cronbach's Alpha? - Explained Simply

Negative Cronbach's alpha???
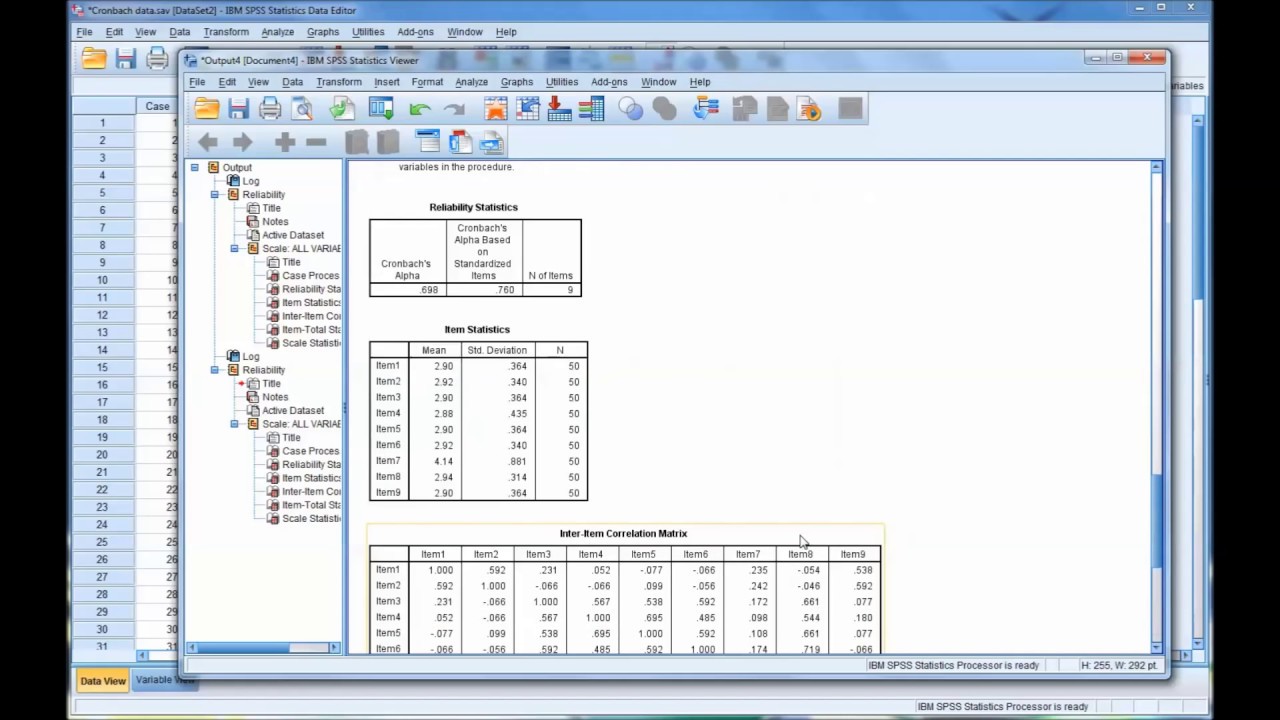
Calculating and Interpreting Cronbach's Alpha Using SPSS

Cronbach's alpha or Coefficient alpha in simple language - DU Professor

Mastering to Increase Cronbach's alpha value | Reliability Test | Simple| using SPSS
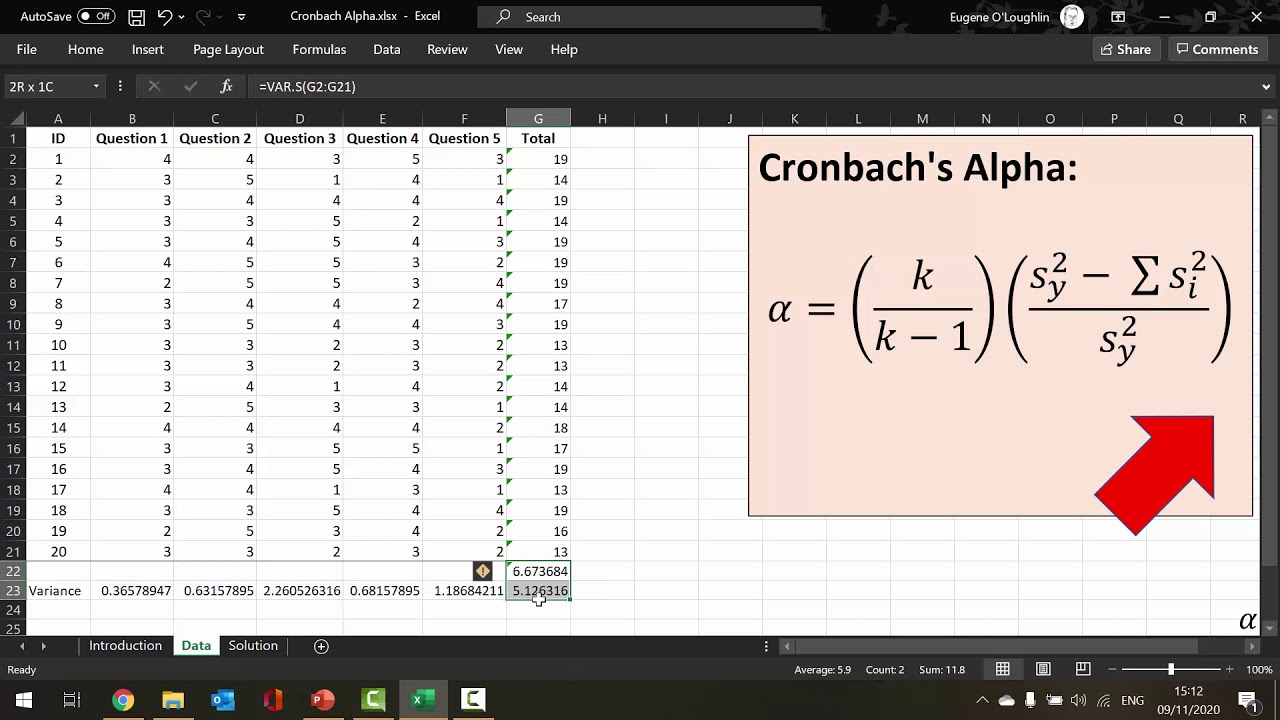
How To... Calculate Cronbach's Alpha in Excel
5.0 / 5 (0 votes)
Thanks for rating: