[Quiz] Regularization in Deep Learning, Lipschitz continuity, Gradient regularization
TLDRThis video script delves into the world of regularization techniques for neural networks, explaining their importance in improving a network's performance and generalization. It begins by defining regularization as a method to enhance the solution to a neural network's objective function. The script uses the analogy of fitting a function through given points to illustrate the concept of overfitting and how regularization terms can enforce smoothness, leading to better generalization. It then discusses two common types of regularization: L1 and L2 (Tikhonov or weight decay), highlighting their differences in penalizing weights. The video also explores Lipschitz continuity, a property that can be enforced through weight clipping to prevent steep changes in the loss function, which is particularly useful when training GANs and defending against adversarial attacks. The script concludes by mentioning advanced regularization techniques that enforce a constant gradient, potentially eliminating local optima and improving training. The host invites feedback and provides additional resources for further learning.
Takeaways
- 📚 **Regularization Defined**: Regularization is a technique used to improve the performance of a neural network by modifying its objective function.
- 🔍 **Objective Function Role**: The objective or loss function guides the neural network on what to learn, while regularization dictates how it should learn it.
- 📈 **Overfitting and Regularization**: Regularization helps to prevent overfitting by discouraging complex models that fit the training data too closely.
- 🟢 **Example of Regularization**: Adding a regularization term can transform an overfit red curve into a generalized green curve that fits the data better.
- 📊 **Common Regularizations**: L1 and L2 (Tikhonov or weight decay) regularizations are commonly used, where L1 adds the absolute sum of weights and L2 adds the squared sum.
- ⚖️ **L1 vs L2 Regularization**: L1 regularization treats all weights equally, while L2 disproportionately penalizes larger weights, leading to a more even distribution of weight sizes.
- 🔧 **Generalization and Simplicity**: Regularization promotes simpler solutions that generalize better by favoring models that do not memorize the training data excessively.
- 🧮 **Lipschitz Continuity**: A function is Lipschitz continuous if the change in output is proportionally limited by the change in input, which can be enforced through weight clipping.
- 🚧 **GANs and Lipschitz**: Lipschitz continuity can help stabilize the training of Generative Adversarial Networks (GANs) by preventing extreme jumps in the discriminator's performance.
- 📉 **Vanishing Gradient Problem**: In GANs, an overly powerful discriminator can lead to a vanishing gradient problem for the generator, which Lipschitz regularization can mitigate.
- 🔄 **Adversarial Attacks**: Lipschitz regularization can defend against adversarial attacks by ensuring that small changes in input do not drastically alter the output.
Q & A
What is the primary purpose of regularization in neural networks?
-Regularization is used to help a neural network solve its objective function more effectively by preventing overfitting and improving generalization to unseen data.
How does the addition of a regularization term affect the loss function?
-The regularization term is added to the loss function, modifying it to not only penalize the error in predictions but also to encourage certain desirable properties in the network's weights.
What is the difference between L1 and L2 regularization?
-L1 regularization adds the absolute sum of the network's weights to the loss term, while L2 (or Tikhonov) regularization adds the sum of the squares of the weights. L1 tends to promote sparsity in the weights, whereas L2 encourages smaller, more evenly distributed weights.
Why is it beneficial to enforce smoothness in the function that a neural network learns?
-Enforcing smoothness can help prevent overfitting by creating a function that generalizes well to new, unseen data. Smooth functions are less likely to make drastic changes in output for small changes in input, which is desirable for robust predictions.
What is Lipschitz continuity, and how does it relate to neural network training?
-A function is Lipschitz continuous if a change in the input value does not cause a change in the output value by more than a certain constant times that input change. In neural networks, enforcing Lipschitz continuity can help prevent extreme changes in outputs for small changes in inputs, which can be useful for stable training and defense against adversarial attacks.
How can weight clipping be used to enforce Lipschitz continuity in a neural network?
-Weight clipping involves setting an upper limit on the absolute value of a network's weights. By clipping weights that exceed this limit, it ensures that the output change due to an input change is bounded, thus enforcing a form of Lipschitz continuity.
Why is it important to have a smooth loss function during the training of a GAN?
-A smooth loss function ensures that small changes in the generator's output do not lead to large jumps in the discriminator's output. This helps avoid vanishing gradient problems and allows for more stable and effective training of the GAN.
What is the advantage of a neural network having a constant gradient in terms of training?
-A neural network with a constant gradient does not have any local optima, as the gradient is never zero. This means that the network can be trained more effectively, as it can always make progress towards a better solution regardless of its current state.
How can Lipschitz regularization help defend against adversarial attacks?
-Lipschitz regularization enforces a limit on how much the output can change with respect to small changes in the input. This makes it more difficult for adversarial attacks to cause a significant shift in the output by only slightly altering the input.
What is the main challenge when training a GAN, and how can regularization techniques help address it?
-The main challenge in training a GAN is the unstable training dynamics, where the discriminator can become too good too quickly, leading to vanishing gradients. Regularization techniques like enforcing Lipschitz continuity can help maintain a smooth loss landscape, allowing for more stable and effective training.
Why might one choose L1 regularization over L2 in certain scenarios?
-L1 regularization can be preferred when sparsity in the weight matrix is desired, as it tends to push many weights to exactly zero. This can lead to a more interpretable model and is useful when feature selection is important.
How does the concept of generalization relate to the choice of regularization technique?
-The choice of regularization technique is closely tied to the concept of generalization. Regularization methods aim to prevent overfitting, which is when a model performs well on training data but poorly on new, unseen data. By promoting generalization, the model can better handle new data and make more reliable predictions.
Outlines
📚 Introduction to Regularization Techniques
This paragraph introduces the concept of regularization in neural networks. The host explains that regularization is a technique to improve how a neural network solves its objective function. It prevents overfitting by enforcing smoothness in the model's output, as illustrated by the example of fitting a function through given points. Two common regularization methods, L1 and L2 (Tikhonov or weight decay), are discussed, with L1 adding the absolute sum of weights to the loss and L2 adding the squared sum. The differences in how they affect weights are highlighted, with L2 shrinking weights more evenly and punishing larger weights more. The benefits of regularization in terms of generalization and preventing overfitting are also covered.
🔍 Advanced Regularization: Lipschitz Continuity
The second paragraph delves into a more advanced regularization technique related to Lipschitz continuity. Lipschitz continuity is defined, and its importance in limiting the rate of change of a function's output in response to changes in input is emphasized. The concept of enforcing Lipschitz continuity through weight clipping is introduced, which caps the maximum absolute value of a weight to prevent sharp output changes. The benefits of this approach in training GANs by avoiding vanishing gradient problems and improving the stability of the discriminator and generator are discussed. Additionally, the paragraph touches on how Lipschitz regularization can mitigate adversarial attacks by ensuring that small input changes do not lead to significant output changes, thereby requiring more noticeable alterations to fool the classifier.
Mindmap
Keywords
💡Regularization
💡Loss Function
💡L1 Regularization
💡Tikhonov Regularization (L2 Regularization)
💡Lipschitz Continuity
💡Weight Clipping
💡Gradient
💡Adversarial Attacks
💡Generalization
💡Overfitting
💡GANs (Generative Adversarial Networks)
Highlights
Regularization is any technique that helps a neural network solve its objective function in a better way.
Regularization is added to the loss function to guide the network on how it should achieve its objective.
The red curve example illustrates overfitting, where a function fits every sample point but generalizes poorly for unseen data.
A regularization term can enforce smoothness, leading to a better generalization as shown by the green curve.
Two common regularizations are L1 and Tikhonov (L2) regularization, which are built into most optimizers like Adam.
L1 regularization adds the absolute sum of all network weights to the loss, while L2 adds the sum of squared weights.
L1 regularization does not prioritize which weights to reduce, focusing on lowering the total weight sum.
L2 regularization shrinks weights more evenly, with higher weights being punished more, leading to better generalization.
Lipschitz continuity ensures that changes in input do not cause disproportionately large changes in output.
A network's Lipschitz constant can be computed, providing an upper limit on the slope of its function.
Weight clipping is a simple method to enforce Lipschitz continuity by setting an upper limit on the absolute value of weights.
Enforcing Lipschitz continuity can help with training GANs by preventing large jumps in the discriminator's performance.
Lipschitz regularization helps prevent vanishing gradient problems by ensuring the loss function changes smoothly.
A better regularization technique than Lipschitz continuity is enforcing a constant gradient, which theoretically eliminates local optima.
Lipschitz regularization can defend against adversarial attacks by ensuring small input changes do not cause large output changes.
Enforcing a low Lipschitz constant makes it harder for adversarial attacks to significantly alter a model's output with minor input perturbations.
The presenter encourages feedback in the comments and provides additional links and sources for further reading.
Transcripts
Browse More Related Video

MIT Introduction to Deep Learning | 6.S191

Deep Learning Crash Course for Beginners

How to Create a Neural Network (and Train it to Identify Doodles)

Ordinary Differential Equations 9 | Lipschitz Continuity [dark version]
Gradient descent, how neural networks learn | Chapter 2, Deep learning
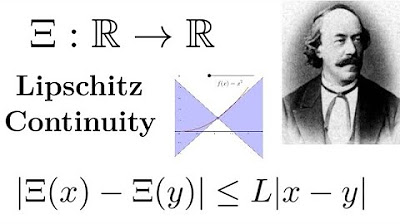
Intro to Lipschitz Continuity + Examples
5.0 / 5 (0 votes)
Thanks for rating: