Chain Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare
7 Jan 201107:41
EducationalLearning
32 Likes 10 Comments

TLDRIn this recitation video, the professor focuses on the application of the chain rule to find two values of theta where the derivative of the function cosine squared theta to the fourth equals zero. The video begins by explaining the meaning of theta in trigonometric functions and the composition of three functions in the given expression. The professor then guides the audience through the process of taking the derivative step by step, using the chain rule. The derivative is expressed in terms of theta by substituting the intermediate variables x and w with their respective expressions in terms of theta. The final expression derived is negative 8 theta to the third times the cosine of theta to the fourth times the sine of theta to the fourth. The video concludes by finding the two values of theta that make the derivative equal to zero, with theta equals zero being the most straightforward solution. The second solution is found by setting the cosine of theta to the fourth equal to zero, which leads to theta being pi over 2 to the 1/4, demonstrating the application of the chain rule in a more complex scenario.

Takeaways
  • đź“š The video focuses on the application of the chain rule to find the derivative of a composite function, specifically cos^2(theta^4).
  • 🎓 Theta (theta) is used as a variable often associated with trigonometric functions and represents an angle measure.
  • 🔍 The function given is a composition of three functions: an outermost squaring function, a cosine function, and an innermost function that raises theta to the fourth power.
  • 🧩 To apply the chain rule, the derivative is found by multiplying the derivatives of the individual functions, from the outermost to the innermost, with respect to their respective variables.
  • 📉 The derivative of cos^2(theta^4) with respect to theta is found to be -8theta^3 cos(theta^4) sin(theta^4).
  • âś‹ The problem requires finding two values of theta where the derivative equals zero.
  • 🔑 An immediate solution is theta = 0, as it makes the entire expression zero.
  • 🧮 To find the second value, consider the cosine function cos(theta^4), which can be zero if theta^4 equals pi/2 or pi/2 + pi.
  • 🔬 Solving theta^4 = pi/2 gives theta = (pi/2)^{1/4}, which is one of the required values.
  • đź“Ś The second value can be found by adding pi to theta, but since only two values are requested, this step is not explicitly shown in the script.
  • đź“ť The process involves understanding the composition of functions and the application of the chain rule to complex functions involving trigonometric identities.
Q & A

  • What is the main topic of the video segment?

    -The main topic of the video segment is the application of the chain rule in calculus to find two values for theta where the derivative of cosine squared theta to the fourth equals zero.

  • What does the variable theta typically represent in trigonometric functions?

    -Theta typically represents the variable that measures angle in trigonometric functions.

  • What does the notation 'cosine squared theta to the fourth' mean?

    -The notation 'cosine squared theta to the fourth' means taking the cosine of theta, raising it to the fourth power, and then squaring the result.

  • What is the first step in solving the given problem?

    -The first step is to take the derivative of the given function with respect to theta using the chain rule.

  • How many functions are composed in the given function?

    -There are three functions composed in the given function: an outermost squaring function, a cosine function, and an innermost function that raises its input to the fourth power.

  • What is the outermost function in the composition?

    -The outermost function in the composition is the squaring function, represented as x squared.

  • What is the derivative of cosine with respect to w?

    -The derivative of the cosine function with respect to w is negative sine of w.

  • What is the derivative of theta to the fourth with respect to theta?

    -The derivative of theta to the fourth with respect to theta is 4 theta to the third.

  • What is the expression for dy/d theta in terms of theta?

    -The expression for dy/d theta in terms of theta is negative 8 theta to the third times cosine of theta to the fourth times sine of theta to the fourth.

  • What is the easiest value for theta that makes the derivative equal to zero?

    -The easiest value for theta that makes the derivative equal to zero is theta equals 0.

  • What is another value for theta that could make the derivative equal to zero?

    -Another value for theta that could make the derivative equal to zero is when theta to the fourth equals pi over 2, which would make the cosine of theta to the fourth equal to zero.

  • How does the chain rule help in finding the values for theta where the derivative is zero?

    -The chain rule helps in finding the values for theta where the derivative is zero by breaking down the composite function into simpler functions and applying the derivative to each part, then combining the results to form the final derivative expression.

Outlines
00:00
đź“š Introduction to the Chain Rule and Problem Statement

This segment of the video introduces the topic of the chain rule and presents a problem to the audience. The professor welcomes the viewers back to recitation and sets the stage for a discussion on the chain rule. The problem involves finding two values for the variable theta such that the derivative of the function 'cosine squared theta to the fourth' equals zero. The professor clarifies that theta typically represents an angle in trigonometric functions and that the function involves squaring the cosine of theta raised to the fourth power. The goal is to apply the chain rule to find the values of theta that satisfy the given condition. The professor also emphasizes the importance of understanding the composition of functions when applying the chain rule, which in this case involves three functions: squaring a function, taking the cosine, and raising to the fourth power.

05:01
🔍 Deriving the Function and Applying the Chain Rule

The professor begins by rewriting the given function to clearly show the composition of three functions: squaring, taking the cosine, and raising to the fourth power. The outermost function is identified as 'x squared', with 'x' being the cosine of 'w', and 'w' being theta to the fourth. The chain rule is then applied, with the professor reminding viewers of the formula dy/d theta = dy/dx * dx/dw * dw/d theta. The derivatives for each part are calculated: dy/dx is 2x, dx/dw is the derivative of the cosine function which is negative sine, and dw/d theta is 4 times theta to the third power. The professor then substitutes 'x' and 'w' with their respective expressions in terms of theta to simplify the derivative. The resulting derivative is a product of three terms, and the problem asks to find where this derivative equals zero. The professor identifies theta equals 0 as an obvious solution and then discusses the more challenging part of finding when the cosine of theta to the fourth equals zero. The solutions involve finding values of theta such that theta to the fourth equals pi/2 or pi, leading to theta being pi/2 to the 1/4 or pi/2 to the 1/4 plus pi, respectively. However, the professor notes that only two values were requested, so the discussion concludes with these solutions.

Mindmap
Keywords
đź’ˇChain Rule
The Chain Rule is a fundamental theorem in calculus used to compute the derivative of a composite function. In the video, the Chain Rule is applied to find the derivative of the function cosine squared theta to the fourth with respect to theta. It's essential for understanding how to break down the complex function into simpler components and compute the derivative step by step.
đź’ˇTheta
Theta (θ) is a Greek letter commonly used in mathematics and physics to denote an angle. In the context of the video, theta represents the variable that measures the angle in trigonometric functions. It's central to the problem as the derivative of the function is taken with respect to theta, and the values of theta that make the derivative zero are sought.
đź’ˇDerivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. In the video, the derivative of the given function is calculated to find the points where the rate of change is zero, which are the solutions to the problem.
đź’ˇCosine Function
The cosine function is a trigonometric function that describes a wave pattern and is often used to model periodic phenomena. In the video, the cosine function is raised to the fourth power and squared, making it a part of the composite function whose derivative is being calculated.
đź’ˇSquared
To square a number means to multiply the number by itself. In the context of the video, 'squared' refers to the operation performed on the cosine of theta to the fourth, which is then squared to form the complete function. This operation increases the complexity of the function and its derivative.
đź’ˇComposite Function
A composite function is a function composed of two or more functions. In the video, the function of interest is a composite of three functions: an outermost squaring function, a cosine function, and an innermost function that raises theta to the fourth power. Understanding the composition is crucial for applying the Chain Rule.
đź’ˇOutermost Function
The outermost function is the function that is on the outside when a composite function is represented in nested form. In the video, the outermost function is 'x squared', where 'x' itself is a function of 'w', and 'w' is a function of theta. Identifying the outermost function is a step in applying the Chain Rule.
đź’ˇInnermost Function
The innermost function is the function that is on the inside when a composite function is represented in nested form. In the video, the innermost function is 'theta to the fourth', which is raised to the power of four. The Chain Rule requires understanding the relationship between the innermost and outermost functions.
đź’ˇDerivative of Cosine
The derivative of the cosine function with respect to its variable is the negative sine function. In the video, when applying the Chain Rule, the derivative of the cosine function is used as one of the components to find the overall derivative of the composite function.
đź’ˇProduct of Functions
In the context of the video, the product of functions refers to the mathematical operation where multiple functions are multiplied together to form a new function. The derivative of the product of the cosine and sine functions, each raised to a power and involving theta, is calculated to find the values of theta that make the derivative zero.
đź’ˇZero Derivative
A zero derivative indicates a point where the rate of change of the function is zero, which often corresponds to a maximum, minimum, or point of inflection. In the video, finding the values of theta that make the derivative of the given function zero is the main goal of the exercise.
Highlights

Introduction to the chain rule and its application in finding values for theta where the derivative equals zero.

Explanation of theta as a variable commonly used in trigonometric functions to represent an angle.

Clarification of the function as cosine of theta to the fourth, squared.

Use of the chain rule to find the derivative of a composite function involving three functions.

Identification of the outermost function as x squared and the subsequent functions in the composition.

Derivation of the derivative dy/dx as 2x for the outermost function.

Derivation of dx/dw as negative sine of w, where w is theta to the fourth.

Calculation of dw/d theta as 4 theta to the third, given w is a function of theta to the fourth.

Substitution of w and x in terms of theta to simplify the derivative expression.

Final expression of the derivative as negative 8 theta to the third cosine of theta to the fourth sine of theta to the fourth.

Identification of theta equals 0 as the simplest solution for the derivative to be zero.

Discussion on the necessity for at least one factor in the product to be zero for the derivative to be zero.

Solution for theta where cosine theta to the fourth equals zero, using the properties of cosine function.

Use of theta equals pi over 2 to the 1/4 as an example to satisfy the condition for the derivative to be zero.

Mention of adding pi to theta to get another solution, but stopping at two solutions as per the question's requirement.

Emphasis on understanding the composition of functions and their derivatives for the application of the chain rule.

Demonstration of how to transform a complex derivative problem into a simpler form by introducing intermediate variables.

Illustration of the process to solve for the derivative of a function composed of three parts, emphasizing the step-by-step approach.

Explanation of how to handle the derivative of a squared trigonometric function, which is a common type of problem in calculus.

Transcripts

Browse More Related Video

Calculus 1: Finding Limits of Trigonometric Functions | Math with Professor V

Trig limit using pythagorean identity | Limits and continuity | AP Calculus AB | Khan Academy

Ex 2: Simplify Trigonometric Expressions

Integrals: Trig Substitution 2

How to Convert From Polar Equations to Rectangular Equations (Precalculus - Trigonometry 40)

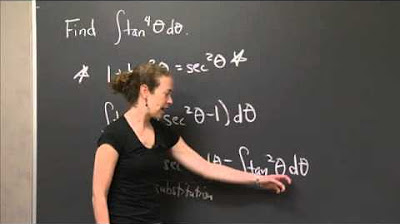
Integral of tan^4 (theta) | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Chain RuleCalculusDerivativeThetaTrigonometryEducationalMathematicsRecitationCosine FunctionZero DerivativeLearning Resource