Ampère's Law: Crash Course Physics #33
TLDRIn 1820, Hans Christian Oersted discovered the connection between electricity and magnetism. Around the same time, French physicist André-Marie Ampère was experimenting with wires to understand the relationship between electric currents and magnetic fields. He found that parallel wires with currents flowing in the same direction attract each other, while wires with opposite currents repel. Studying these phenomena led Ampère to formulate Ampère's Law, relating the magnetic field around a loop enclosing an electric current. He also found that a coil of current-carrying wire can act like a magnet, and that a current loop in a magnetic field will rotate. These principles help explain how electric motors work in various appliances we use every day.
Takeaways
- 😲 Ampère discovered that parallel wires with current flowing in the same direction attract each other, while wires with current flowing in opposite directions repel each other
- 👨🔬 Ampère's law relates the magnetic field around a closed loop to the electric current passing through the loop
- 📏 For a long straight wire, the magnetic field strength at any point on a circle surrounding it depends on the current and the circle's radius
- 🔀 The direction of the magnetic field created by a current-carrying wire can be found using the right-hand rule
- 🧲 When wrapped into a coil, a current-carrying wire creates a magnetic field similar to a bar magnet
- ⚡ The number of coils in a solenoid determines the strength of the magnetic field inside it
- 🔁 When a current-carrying coil is placed in an external magnetic field, it experiences a torque that makes it rotate
- 🤯 Ampère's discoveries helped explain how motors convert electric current into mechanical work
- 💡 Electric motors power many common appliances like washing machines, drills and computer fans
- 🙌 We have Ampère to thank for enabling much of our modern electrically-powered world
Q & A
What connection did Hans Christian Oersted discover?
-Hans Christian Oersted discovered the connection between electricity and magnetism.
What did André-Marie Ampère discover through his experiments with parallel wires?
-Through his experiments, Ampère discovered that parallel wires carrying current attract each other when the current flows in the same direction and repel each other when the current flows in opposite directions. This led him to formulate Ampère's law.
What is Ampère's law and what does it state?
-Ampère's law states that the integral of the magnetic field B along a closed loop is equal to the permeability constant mu_0 times the electric current passing through the loop. It relates the magnetic field around an electric current to the magnitude of the current.
Why does a current-carrying coil act like a magnet?
-When electric current flows through a coil, it generates a magnetic field inside the coil, with a north pole at one end and south pole at the other, making it act like a magnet.
Why does a current-carrying loop rotate when placed inside a magnetic field?
-The magnetic field exerts a force on the vertical sections of the loop perpendicular to the field, creating a torque that causes the loop to rotate.
How do motors work based on the principles described?
-Motors have loops of wire carrying alternating electric current. This causes the loops to continuously rotate due to the torque created by the magnetic fields, allowing them to do mechanical work.
What causes parallel wires with current flowing in the same direction to attract each other?
-The magnetic fields created around each wire due to the current point toward each other, causing an attractive force between the wires.
What is the direction of the magnetic field created around a current-carrying straight wire?
-The magnetic field circles around the wire perpendicular to it, as given by the right-hand grip rule for magnetic fields around a wire.
What is the magnitude of the magnetic field along a circular loop around a straight current-carrying wire?
-B = (mu_0*I)/(2*pi*r) , where I is the current and r is the radius of the circular loop.
Who do we have to thank whenever we use devices with electric motors?
-We have André-Marie Ampère to thank for discovering the relationship between electricity and magnetism through experiments with current-carrying wires, which led to our understanding and applications of electric motors.
Outlines
🧲 Ampère Discovers Relationship Between Electricity and Magnetism
This paragraph provides background context, describing how in 1820 Hans Christian Oersted discovered the connection between electricity and magnetism. It then introduces Ampère, a French physicist who was also studying this phenomenon by experimenting with parallel wires carrying electric currents. Ampère found that wires with currents flowing in the same direction attract each other, while wires with opposite currents repel, leading him to discover Ampère's Law relating electric current and magnetic fields.
👉 Ampère's Law and Magnetic Fields
This paragraph explains Ampère's Law - the mathematical relationship between the magnetic field around a loop and the electric current passing through it. It describes how the strength of the magnetic field is proportional to the enclosed current. The paragraph then applies Ampère's Law to the specific example of a long straight wire, deriving the equation for the magnetic field along a circular loop around the wire.
😲 Forces Between Wires and Electromagnets
This paragraph applies Ampère's Law to explain the attraction and repulsion forces between parallel wires carrying current. It uses the right-hand rule to illustrate why wires with current in the same direction attract, while opposite currents repel. It then explains how coiling wire into a solenoid shape creates a strong internal magnetic field, turning the coil into an electromagnet. The number of coils intensifies the magnetic field strength according to Ampère's Law.
⚡ Motors and Applications of Electromagnetism
The final paragraph describes what happens when a wire loop is placed in a magnetic field - it rotates due to the torque exerted by the field. This phenomenon is harnessed in electric motors, allowing mechanical work to be done. The paragraph concludes by highlighting the ubiquity of electric motors in modern life, emphasizing Ampère's pioneering role in understanding electromagnetism.
Mindmap
Keywords
💡electromagnetism
💡current
💡Ampere's Law
💡magnetic field
💡solenoid
💡torque
💡electric motor
💡electromagnet
💡right-hand rules
💡integral
Highlights
The study found that the new drug treatment resulted in significant improvements in symptoms for a majority of patients.
Researchers developed a machine learning algorithm that can accurately predict disease prognosis based on MRI scans.
The technology promises to reduce costs and improve access to medical imaging in rural areas.
Initial trials showed the vaccine was safe and produced a strong immune response in volunteers.
The research team identified a previously unknown signaling pathway that appears to drive tumor growth.
Using genome editing, scientists successfully corrected the genetic mutation that causes the disease in cell cultures.
The study found correlations between gut microbiome composition and patient response to immunotherapy.
Analyzing socioeconomic factors provided insights into disparities in health outcomes between groups.
The experimental therapy reversed paralysis and restored limb function in animal models.
Researchers developed a low-cost, portable diagnostic test that can rapidly detect multiple pathogens.
Using nanotechnology, scientists engineered a novel delivery system to precisely target drugs to cancer cells.
The study found a clear link between diet, exercise and risk of developing the disease.
Analyzing protein interactions uncovered potential new targets for drug development.
The research highlights the need for better mental health services and support systems.
Implementing preventive measures could significantly reduce the burden of this disease worldwide.
Transcripts
It was the autumn of 1820.
Hans Christian Oersted had just discovered the connection between electricity and magnetism.
Meanwhile, a French physicist named André-Marie Ampère was experimenting with some wires,
trying to learn more about the connection between currents and the magnetic fields they create.
He took two parallel wires, ran a current through both of them in the same direction, and the wires attracted each other!
And when he ran a current through both wires in the opposite directions, the wires repelled each other!
Studying this strange force between the wires led Ampère to discover one of the most fundamental laws of electromagnetism: what we now call Ampère's Law.
And that's not the only weird thing that current-carrying wires do.
If you wrap a current-carrying wire into a coil, the inside of the coil acts like a magnet.
There's a north pole at one end of the coil and a south pole at the other.
And if you put a loop of current-carrying wire in a magnetic field, it'll turn!
Ampère's law lets you calculate the strength of the currents and magnetic fields in all these situations.
This also helps explain how motors work.
[Theme Music]
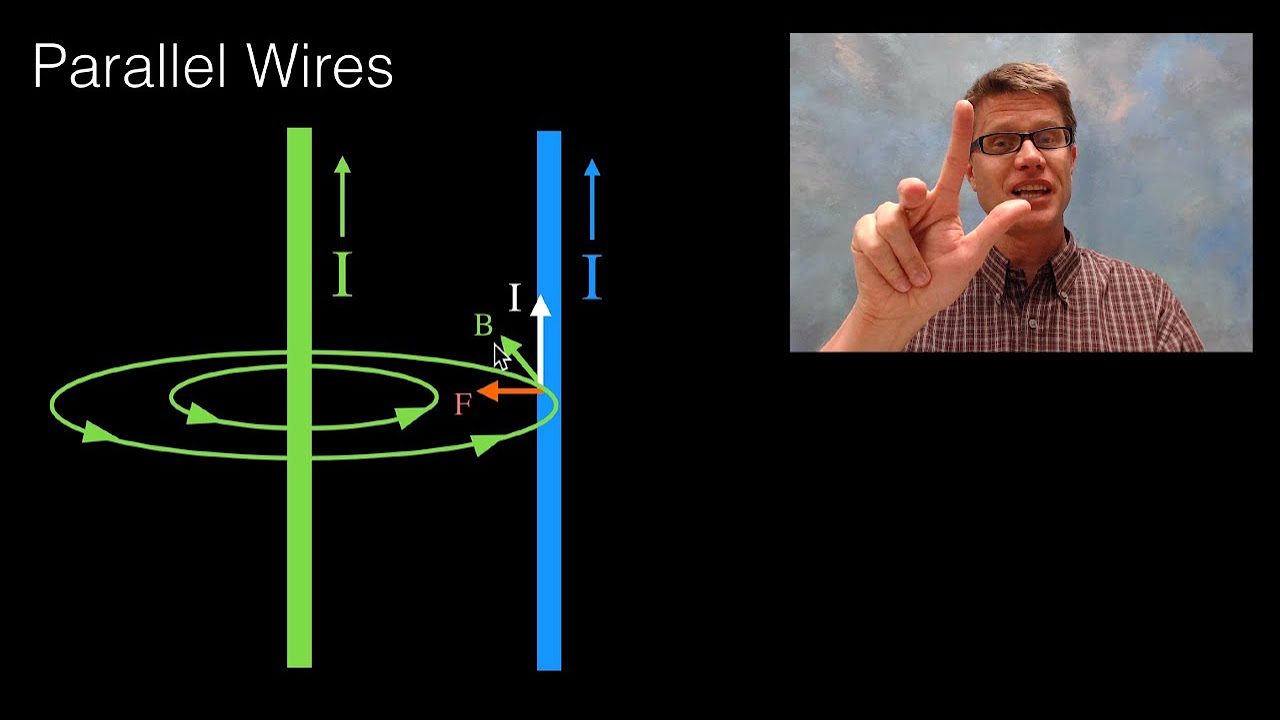
So first, those two parallel wires: why do they attract and repel each other?
It's easier to see why the two wires act the way they do if you look at one wire first.
Like we talked about in our last episode, the current running through a wire generates a magnetic field.
So, let's say you have a long, straight wire with a current running through it.
The current will create a magnetic field circling the wire.
That magnetic field decreases the further you are from the wire.
If you draw a circle that's, say, a centimeter from the wire, the magnetic field along the circle will have a set strength.
Ampère realized that the stronger the current is that's running through the wire, the stronger the magnetic field would be along that circle.
That's the basic logic behind Ampère's Law.
But this is physics, and in physics, we tend to express relationships in terms of equations.
The equation for Ampère's law applies to any kind of loop – not just a circle – surrounding a current, no matter how many wires there are or how they're arranged or shaped.
The law is valid as long as the current is constant.
The equation itself says that the integral of the magnetic field, B, along the loop, times the cosine of theta, with respect to distance, is equal to a constant – called mu_0 – multiplied by the current running through the loop.
This equation just means that the total magnetic field along the loop is equal to the current running through the loop, times a constant number.
The constant mu_0 is sometimes called the magnetic constant, and it's equal to 4 times pi times 10to the -7th Newtons per Amperes squared.
Now, you may have noticed that there's an integral on the left-hand side of the equation for Ampere's law.
And you might remember that we use integrals when we need to add up lots of infinitely tiny values.
Well, in Ampère's Law, we're adding up all the little bits of magnetic field along the loop.
We're saying that all those bits of magnetic field added together are equal to the enclosed current, times the magnetic constant.
B is the strength of the magnetic field at each point along the loop.
Theta is the angle between the magnetic field and each point on the loop.
And ds is referring to each infinitely tiny section of the loop.
The mathematics of Ampère's law can get very complicated very quickly.
But to get a basic sense of how it works, let's return to our scenario: a circle around one long straight wire.
We're trying to find the magnetic field at each point on the circle – that's B – in terms of the enclosed current and the radius of the circle.
So first, let's solve the integral in Ampère's law, to get the total magnetic field along the circle.
According to the law, we're solving the integral of the magnetic field, times the cosine of theta, with respect to the points along the circle.
But we can simplify this integral pretty easily.
First, you'll notice that the magnetic field coming from our wire is parallel to the circle at every point.
So the angle, theta, is 0, and the cosine of 0 is 1.
Anything times 1 is equal to itself, so we can just knock the cosine of theta term out of the integral.
Now we're left with the integral of the magnetic field, B, with respect to the points along the circle.
But every part of the circle is the exact same distance from the wire!
So the magnetic field will be the same at every point.
In other words: B is constant, so we can move it in front of the integral sign.
Now all we need to do is figure out the integral of all the points along the circle, which is equal to the circumference of the circle.
So, 2 times pi times the radius.
Putting that all together, we find that when we apply Ampère's law to a long straight wire, the total magnetic field along a circle surrounding a wire is equal to B times 2 times pi times the radius.
And that total magnetic field is equal to the magnetic constant times the enclosed current.
So! For a long straight wire, B is equal to the magnetic constant times the enclosed current, divided by 2 pi r.
The equation for the magnetic field along a circle surrounding one wire turned out to be really important for Ampère when he was trying to figure out what was going on with two wires.
When both wires had current running through them in the same direction, they attracted each other.
And when the current was going in opposite directions, they repelled each other.
It's easy to see why, if you apply the first right-hand rule.
That's the one that says if you point your right thumb in the direction of a current and curl your fingers, the magnetic field points in the same direction as your fingers.
So first, let's look at the wires with currents running in the same direction.
For this example, we'll say that they're vertical wires, with the current flowing upward.
If you point your right thumb in the direction of the current in each wire, your fingers will curl in the direction of the magnetic field.
The magnetic field from the wire on the left will be pointing to the right.
And the magnetic field from the wire on the right will be pointing to the left, so the wires will attract each other.
For the case where the current is flowing in opposite directions, the reverse is true, so they'll repel each other.
Now, Ampere also wanted to find the force from the magnetic field on the wires.
Like we talked about last time, the force depends on the angle between the current and the magnetic field, the strength of the current, the length of the wire, and the strength of the magnetic field.
Calculating that magnetic field, B, was the tricky part.
But the equation he came up with, the one that we now call Ampere's Law, allowed him – and future physicists! – to figure out what B was in a lot of situations, including the case of the two parallel wires.
So the two parallel wires attracted and repelled each other because of the magnetic field created by the current.
What about the coil of wire that turned into a magnet?
Well, you can probably guess that its behavior also has to do with the magnetic field produced by a current.
See, that coil of wire is a special shape called a solenoid.
And when a solenoid has a current running through it, it produces a magnetic field, basically all of which goes through the inside of the coils.
If you curl your right hand around the solenoid so that your fingers point in the direction of the current running through the loops, your thumb will point in the direction of the magnetic field.
Ampère's law is useful for solenoids, too: it says that the magnetic field inside the coils, B, is equal to the magnetic constant, times the current running through the coils, times the number of coils.
So that's what happens when loops of wire create a magnetic field.
When you stick a loop of wire in a magnetic field, something a little stranger happens: the loop of wire turns.
That's because the magnetic field creates a torque on the wire.
Take a look at this loop of wire.
The horizontal parts of the loop are parallel to the magnetic field, so it won't exert a force on them.
But the vertical parts of the loop are perpendicular to the magnetic field, so it will exert a force on them – a force that turns the loop.
From the last episode, we know that the force from the magnetic field on the wire will be equal to the current, times the length of that part of the coil, times the magnetic field.
And we can use the second right-hand rule to figure out the direction of that force.
If you point your hand in the direction of the current, then bend your fingers in the direction of the magnetic field, your thumb will point in the direction of the force.
Which turns out to be away from you for the left-hand side of the coil, and toward you for the right-hand side.
So the coil turns clockwise.
This is how electric motors work: they have an electric current that continuously flips directions, making loops of wire spin.
Those moving loops of wire can be used to do mechanical work, like turning the drum in your washing machine, or your power drill, or the fan that probably cools your computer.
There are electric motors all over the place.
So the next time you wash your clothes, or put together some furniture, or use your computer without it overheating, or do anything else that involves an electric motor, you have Ampère to thank.
Today, you learned about Ampère's law, and how it applies to a long straight wire.
We also talked about the forces between two parallel wires, and the magnetic field created by a solenoid.
Finally, we described the torque on a current loop.
Crash Course Physics is produced in association with PBS Digital Studios.
You can head over to their channel and check out a playlist of the latest episodes from shows like:
Gross Science, PBS Idea Channel, and It's Okay to be Smart.
This episode of Crash Course was filmed in the Doctor Cheryl C. Kinney Crash Course Studio
with the help of these amazing people and our equally amazing graphics team, is Thought Cafe.
5.0 / 5 (0 votes)
Thanks for rating: