Lesson 1 - Basic Trig Identities Involving Sin, Cos, and Tan
TLDRThis transcript outlines a comprehensive lesson plan for a trigonometry and precalculus tutorial, emphasizing the importance of mastering essential mathematical techniques for success in higher-level courses like calculus and sciences. The tutor introduces the concept of trigonometric identities, which are fundamental relations used to simplify and solve trigonometric equations. The 'trig rainbow' is a mnemonic device presented to help students remember the relationships between sine, cosine, tangent, cotangent, secant, and cosecant. The lesson demonstrates how to prove and apply these identities, using them to solve equations and simplify expressions. The goal is not to memorize every identity but to become comfortable with their usage, allowing students to tackle complex problems with confidence in future studies.
Takeaways
- 📚 Start with the basics: The importance of understanding fundamental trigonometric functions like sine, cosine, and tangent in the context of both triangles and the unit circle.
- 🌈 The Trig Rainbow: A mnemonic device to remember the relationships between the primary trigonometric functions (sine, cosine, tangent) and their reciprocals (cosecant, secant, cotangent).
- ↔️ Reciprocal Relationships: Sine is the reciprocal of cosecant, cosine is the reciprocal of secant, and tangent is the reciprocal of cotangent, which are key to simplifying trigonometric expressions.
- 🔢 Trigonometric Identities: Learning to use and prove essential trigonometric identities that are vital for solving more complex problems in calculus and other STEM fields.
- 📈 Building Skills: The necessity of practicing with trigonometric identities to build proficiency, which will be beneficial for advanced courses like calculus and physics.
- 📝 Practice and Review: Encouragement to practice by working through problems in the lessons, reviewing the material, and seeking additional practice in textbooks.
- 📈 Progression of Lessons: The lessons are designed to build upon previous knowledge, starting with fundamental concepts and moving towards more complex applications.
- 🔁 Use of Trigonometric Functions: Understanding how to rewrite trigonometric functions in terms of each other using the Trig Rainbow, which simplifies problem-solving.
- 📋 Memorization vs. Application: The goal is not to memorize every identity but to become comfortable with them, knowing how and when to apply them effectively.
- 🔍 Understanding the Proof Process: Learning how to prove trigonometric identities by transforming one side of an equation to match the other using algebraic and trigonometric properties.
- 🧩 Pieceing Together Solutions: Recognizing that solving trigonometric problems often involves multiple steps and the use of various identities to reach a simplified and solvable form.
Q & A
What is the main focus of the second volume of the Trigonometry and Precalculus tutor?
-The main focus of the second volume is to continue building essential skills in trigonometry and precalculus, with a significant emphasis on trigonometric identities, which are crucial for success in calculus and other STEM fields.
Why are trigonometric identities important in solving trigonometric equations?
-Trigonometric identities are important because they can help simplify complex equations involving trigonometric functions, making them easier to solve and allowing for the cancellation of terms or the transformation of expressions into more manageable forms.
What is the 'trig rainbow' and how does it help in remembering trigonometric identities?
-The 'trig rainbow' is a mnemonic device that lists trigonometric functions in a logical order, helping to visualize and remember the relationships between them. It aids in recalling that sine is to cosecant as cosine is to secant, and tangent is to cotangent, allowing for easy derivation of fundamental trigonometric identities.
What are the three fundamental trigonometric identities that can be derived from the trig rainbow?
-The three fundamental identities are: sine of theta equals 1 over cosecant of theta, cosine of theta equals 1 over secant of theta, and tangent of theta equals 1 over cotangent of theta.
How does the concept of the unit circle relate to the definitions of sine, cosine, and tangent?
-The unit circle is a circle with a radius of 1 centered at the origin. The definitions of sine, cosine, and tangent are derived from the coordinates of a point on the unit circle corresponding to a given angle. Sine represents the y-coordinate, cosine the x-coordinate, and tangent is the ratio of sine to cosine.
What is the purpose of the law of sines and the law of cosines in mathematics and science?
-The law of sines and the law of cosines are used to solve for unknown angles and side lengths in triangles, particularly non-right triangles. They are fundamental in various branches of mathematics, science, and engineering for problems involving triangles and spherical geometry.
Why is it recommended to watch the lessons in sequence and practice solving problems?
-Watching the lessons in sequence ensures that learners build on previously learned concepts and gradually develop a deeper understanding of trigonometry and precalculus. Practicing problem-solving helps reinforce the concepts, improves the ability to apply them, and prepares students for more complex problems in advanced courses.
How does the concept of the unit circle help in understanding the relationship between sine and cosine?
-The unit circle provides a geometric interpretation of sine and cosine. For any angle, the sine is represented by the y-coordinate and the cosine by the x-coordinate of the point where the terminal side of the angle intersects the unit circle, illustrating their correlation and periodic nature.
What is the significance of understanding the relationship between tangent and cotangent?
-Understanding the relationship between tangent and cotangent is significant because it allows for the simplification of trigonometric expressions and the solving of equations involving these functions. Knowing that tangent is sine over cosine and cotangent is cosine over sine helps in transforming and manipulating trigonometric equations.
Why is it suggested to review the first volume of the Trigonometry and Precalculus tutor before starting the second volume?
-Reviewing the first volume is important because it covers essential skills and concepts that are foundational for the second volume. Without a solid understanding of topics such as the unit circle, complex numbers, and graphing, learners may struggle to grasp the more advanced material presented in the second volume.
How can the trigonometric identities be used to prove other trigonometric identities?
-Trigonometric identities can be used to prove other identities by substituting known relationships and using algebraic manipulations. This process involves applying the identities to one side of an equation to transform it into an equivalent form that matches the other side, thereby proving the identity.
Outlines
📚 Introduction to Trigonometry and Precalculus Tutor Volume 2
This paragraph introduces the second volume of a trigonometry and precalculus tutorial series. The speaker emphasizes the importance of mastering essential techniques for success in precalculus, trigonometry, and higher-level calculus courses. It is mentioned that the lessons will focus on trigonometric identities, which are fundamental in various mathematical disciplines. The paragraph also advises new students to review volume one to ensure they have a grasp on basic concepts before proceeding.
🌈 The Trig Rainbow: Visualizing Trigonometric Functions
The speaker introduces the 'Trig Rainbow', a mnemonic device to help remember the relationships between trigonometric functions. By listing the functions in a specific order (sine, cosine, tangent, cotangent, secant, cosecant), the speaker shows how each function can be expressed in terms of its reciprocal. This method simplifies the memorization of identities and provides a visual aid for understanding and solving trigonometric problems.
🔢 Fundamental Trigonometric Identities and Problem Solving
This paragraph delves into the fundamental identities derived from the Trig Rainbow and their applications. The speaker clarifies that while there are six identities presented, only three are fundamental, with the others being derived from them. The paragraph also discusses the definition of the tangent function and its relation to sine and cosine. The speaker demonstrates how to manipulate these identities to solve trigonometric equations, emphasizing the importance of understanding rather than memorizing these relationships.
📉 Proving Trigonometric Identities through Substitution
The speaker illustrates the process of proving trigonometric identities using algebraic manipulation and substitution. By starting with a given identity, the speaker shows how to work with one side of the equation to demonstrate its equivalence to the other side. The examples provided involve simplifying expressions using the Trig Rainbow identities. The goal is not to memorize every identity but to become comfortable with their application in solving problems.
🚀 Applying Trigonometric Identities in Advanced Mathematics
In this paragraph, the speaker discusses the application of trigonometric identities in more complex problems and their importance in higher-level mathematics courses, including calculus. The focus is on becoming proficient with identities to the point where students can effectively use them without being intimidated by their complexity. The speaker encourages students to practice and become familiar with these identities to enhance their problem-solving skills for future mathematical challenges.
Mindmap
Keywords
💡Trigonometry
💡Precalculus
💡Trigonometric Identities
💡Unit Circle
💡Sine, Cosine, and Tangent
💡Trig Rainbow
💡Law of Sines and Cosines
💡
💡Proof
💡Cotangent
💡Secant
💡Cosecant
Highlights
The course continues from where Trigonometry and Precalculus Volume 1 ended, focusing on essential techniques for success in precalculus, trigonometry, and beyond.
Trigonometric identities, which are proven relations, are a significant focus of the course and are crucial for solving equations involving trig functions.
The importance of understanding the unit circle, complex numbers, and graphing trig functions as foundational knowledge for the course.
The 'Trig Rainbow' is introduced as a mnemonic device to remember the relationships between trigonometric functions.
Sine of an angle is equivalent to 1 over the cosecant of the same angle, a fundamental trig identity.
Cosine is related to secant, and tangent to cotangent, with these relationships forming the basis of the Trig Rainbow mnemonic.
The course emphasizes the importance of not just memorizing identities, but understanding how to apply them in problem-solving.
The tangent function is defined as sine over cosine, a fundamental concept derived from the unit circle and triangle definitions.
Cotangent is the reciprocal of tangent, represented as cosine over sine, which is a direct result of the Trig Rainbow mnemonic.
The course will cover how to prove trig identities, such as cosine times secant equals one, using logical substitutions.
Sine times secant equals tangent is another example of an identity that students are expected to prove using trigonometric relations.
The course aims to build comfort with trig identities so that students can effectively use them in more complex problems.
The Trig Rainbow mnemonic is a tool to help students remember the fundamental relationships between trigonometric functions without memorization.
The course will progressively introduce more complex identities and practice problems to prepare students for calculus and other advanced math courses.
Students are encouraged to practice solving problems on their own and consult textbooks for additional practice after each lesson.
The goal of the course is to ensure students have a strong foundation in trigonometry and precalculus to excel in calculus and related fields.
The Trig Rainbow mnemonic is a practical application that can be used in advanced math and science classes, including when dealing with complex problems.
Transcripts
Browse More Related Video
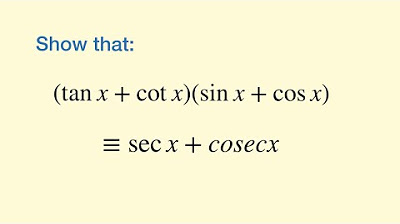
Secant, Cosecant and Cotangent - (2 of 4: Trigonometric Identities)

Derivatives of Trig Functions (Sin, Cos, Tan) in Calculus - [1-4]

Ultimate trig identity problem study guide!

Trig - 0.4 Fundamental Trig Identities
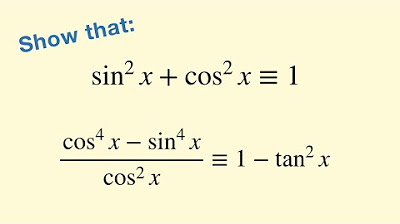
Intro to Trigonometric Identities - part 1

Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial
5.0 / 5 (0 votes)
Thanks for rating: