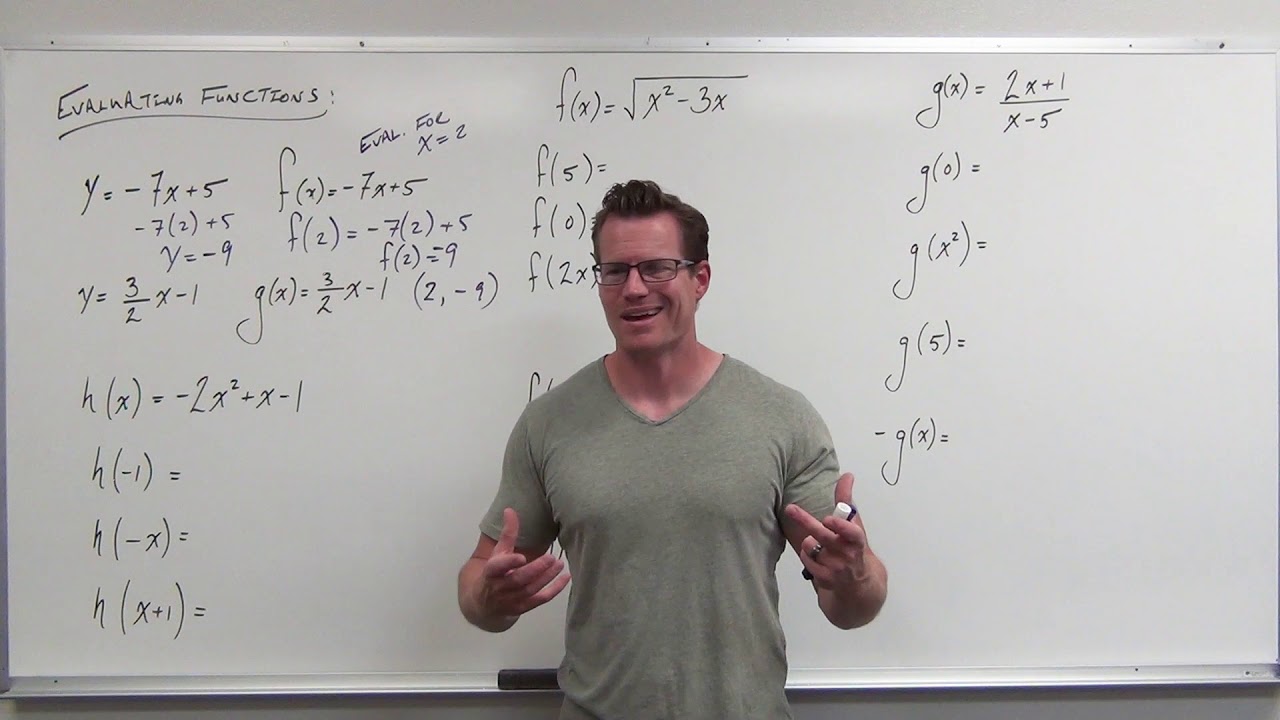Calculus Teacher explains why trigonometry is important for Calculus
TLDRThe video script discusses the transition from algebra to precalculus and then to calculus, emphasizing the importance of understanding trigonometric identities and abstract thinking. It highlights how precalculus serves as a stepping stone, introducing variables treated as trigonometric functions, which prepares students for the complexities of calculus. The script also touches on the concept of limits and how calculus deals with infinitely small quantities, a concept that was historically challenging but has been overcome with clever mathematical methods. Additionally, it mentions the relevance of vector mathematics in physics and its integration into advanced calculus. The speaker encourages students to invest time and effort into precalculus to develop higher-level thinking skills and to ask questions to deepen their understanding.
Takeaways
- 📐 **Trigonometric Identities:** Precalculus introduces students to trigonometric identities, which are crucial for understanding calculus and solving more complex equations involving trigonometric functions.
- 🧮 **Abstraction in Precalculus:** The shift from algebra to precalculus involves treating trigonometric functions as variables, which adds a layer of abstraction and prepares students for the abstract thinking required in calculus.
- 🔢 **Algebraic Foundations:** Precalculus builds upon algebraic skills, teaching students to work with variables and functions, including the application of the Pythagorean theorem.
- 🔑 **Law of Cosines:** The script discusses the application of the law of cosines in solving triangles, which is a practical example of how precalculus concepts are applied.
- 🚀 **Transition to Calculus:** Precalculus serves as a stepping stone to calculus, where students will combine their knowledge of algebra and trigonometric functions with new concepts like limits.
- 📉 **Limits and Infinitesimals:** Calculus involves the concept of limits, particularly when dealing with functions that approach zero, which is a significant shift from traditional algebraic operations.
- 🔄 **Newton's Method:** The script mentions Newton's approach to handling situations where both the numerator and denominator approach infinity, which is a fundamental concept in calculus.
- 🤔 **Understanding Abstract Concepts:** Students are encouraged to embrace abstract thinking, which is essential for grasping more complex mathematical ideas in calculus.
- 🤓 **Familiarity with Trigonometric Functions:** Becoming comfortable with trigonometric functions in precalculus makes the transition to calculus smoother, as these functions are frequently used in calculus problems.
- 📚 **Vector Applications:** The study of vectors in precalculus is not only important for physics but also lays the groundwork for vector calculus, which is a significant part of higher-level mathematics.
- 💡 **Conceptual Challenges:** The script emphasizes the importance of understanding how to conceptualize and solve problems involving very small or infinitely small quantities, which is a key aspect of calculus.
Q & A
What is the significance of trigonometric identities in the transition from precalculus to calculus?
-Trigonometric identities are crucial as they represent an additional layer of abstraction beyond algebra. They prepare students to treat trigonometric functions as variables, which is essential for calculus where functions are manipulated and limits are considered.
How does the concept of dealing with variables in precalculus differ from calculus?
-In precalculus, students deal with trigonometric functions as variables, whereas in calculus, they deal with the rates of change and limits, often represented through algebraic manipulations but with an emphasis on the concept of infinity.
What is the role of the Pythagorean theorem in the context of precalculus and calculus?
-The Pythagorean theorem is foundational in understanding relationships between sides of a right triangle. In precalculus, it's used with variables, while in calculus, it can be applied in more complex contexts, such as when dealing with limits and rates of change.
How does the concept of limits relate to the idea of infinity in calculus?
-In calculus, limits are used to understand the behavior of functions as the input approaches a certain value, often infinity. This concept allows for the manipulation of expressions that would otherwise be undefined, such as division by zero.
What is the importance of understanding abstract concepts in precalculus for future studies in calculus?
-Understanding abstract concepts in precalculus is vital as it prepares the mind for higher-level thinking required in calculus. It helps students to think of functions not just as variables, but as entities that can change and be manipulated in complex ways.
How does the concept of vectors relate to the study of physics and calculus?
-Vectors are essential in physics for describing forces and motions in multiple dimensions. In calculus, vector calculus extends the methods of calculus to vector fields, which has applications in physics and engineering.
What is the challenge students face when dealing with the idea of both the numerator and denominator approaching zero in calculus?
-The challenge lies in understanding how to handle expressions where both parts are getting infinitely small. Traditional arithmetic rules do not apply, and students must learn new concepts such as limits to make sense of these scenarios.
How did Sir Isaac Newton contribute to the understanding of calculus?
-Newton developed the concept of fluxions, which is an early approach to calculus that deals with the rates of change and the idea of infinitesimals. His work laid the foundation for modern calculus, particularly in handling expressions involving infinitesimals.
What is the purpose of learning trigonometric identities in precalculus?
-Trigonometric identities are essential for solving more complex trigonometric equations and for understanding the relationships between different trigonometric functions. They are also used in calculus, where a solid understanding of these identities can simplify problem-solving.
Why is it important to become comfortable with abstract thinking in precalculus?
-Becoming comfortable with abstract thinking is important because it prepares students for the abstract nature of calculus, where they will encounter concepts like limits and infinitesimals, which require a higher level of abstraction than precalculus.
How does the study of precalculus serve as a stepping stone to higher-level thinking skills?
-Precalculus introduces students to more abstract concepts than algebra, such as treating functions as variables and understanding vector operations. These skills are foundational for advanced mathematics and physics, making precalculus a crucial stepping stone.
What advice would you give to students who are struggling with the abstract concepts in precalculus?
-Encourage students to invest time and effort into understanding these concepts, ask questions, and seek help when needed. Emphasize that the struggle with abstraction is a normal part of the learning process and that persistence will lead to a deeper understanding of the material.
Outlines
📚 The Transition from Algebra to Calculus via Precalculus
This paragraph discusses the progression from algebra to calculus through precalculus. It emphasizes the importance of trigonometric identities and how they are treated as variables in precalculus, which is a step towards the abstraction required for calculus. The speaker explains that in precalculus, students learn to solve equations with trigonometric functions instead of simple variables, which prepares them for the concept of limits in calculus. The transition involves thinking of functions as variables, which is a significant cognitive shift. Calculus is described as primarily algebra with the introduction of limits and the concept of infinitely small quantities. The speaker also touches on the historical development of calculus and how it deals with division by zero through the use of limits.
🚀 The Relevance of Vectors in Physics and Advanced Mathematics
The second paragraph delves into the application of vectors, not only in precalculus but also in physics and advanced calculus. It highlights how vector mathematics is fundamental in understanding physical phenomena such as force and torque. The speaker mentions that in the third semester of calculus, students will perform calculus operations on vectors, indicating the interconnectedness of mathematical concepts. The paragraph also encourages students to invest time and effort into understanding precalculus, as it serves as a stepping stone to higher-level thinking skills. The speaker poses a question about the concept of limits as a variable approaches zero, which is a fundamental concept in calculus, and acknowledges the historical ingenuity humans have shown in dealing with mathematical infinities.
Mindmap
Keywords
💡Trigonometric Identities
💡Abstraction
💡Pythagorean Theorem
💡Law of Cosines
💡Quadratic Equations
💡Calculus
💡Limits
💡Vector Calculus
💡Physics
💡Infinity
💡Derivatives
Highlights
Trigonometric identities are a key component in the transition from algebra to precalculus and then to calculus.
In precalculus, students learn to deal with trigonometric functions as variables, adding a layer of abstraction.
Solving equations with trigonometric functions prepares students for calculus concepts.
The law of cosines is used to solve ambiguous triangles, which is a significant step towards understanding calculus.
Calculus is predominantly algebra, but introduces the concept of limits and infinitesimals.
Understanding limits involves dealing with expressions where both the numerator and denominator approach zero.
Isaac Newton developed methods to handle cases where the numerator and denominator both become infinitely small.
Precalculus training with abstract concepts makes calculus less daunting.
Trigonometric identities learned in precalculus are essential for calculus.
Vector mathematics is not only used in physics but also in advanced calculus.
Vectors are integrated into calculus in the third semester, where calculus operations are performed on them.
Precalculus serves as a stepping stone to higher-level thinking skills and is integral to various fields.
Students are encouraged to invest time and effort into precalculus for its long-term benefits.
The concept of infinity and limits is introduced from the very first day in calculus.
Human ingenuity over centuries has led to clever ways to deal with mathematical infinities.
The speaker emphasizes the importance of asking questions to fully grasp the concepts.
The material covered in precalculus and calculus has practical applications in fields like physics.
The interconnectivity of precalculus, calculus, and physics is highlighted as beneficial for a comprehensive understanding.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: