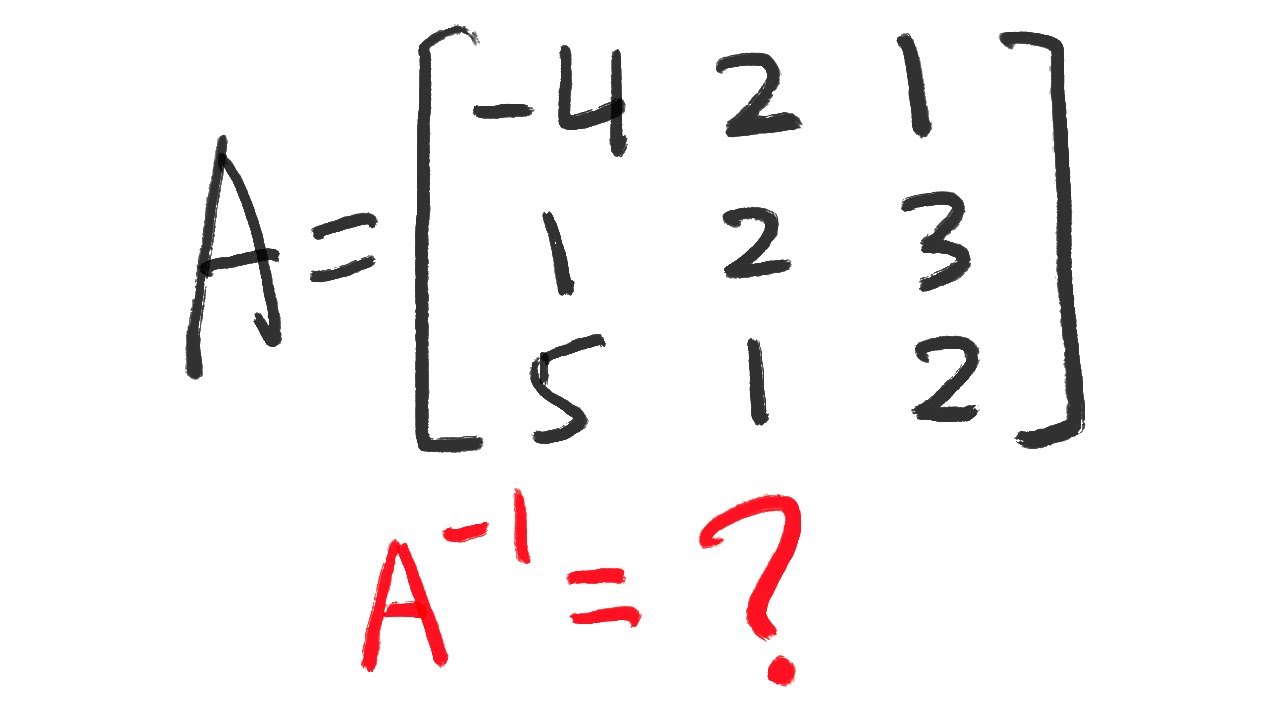How to find The Inverse of a (3 × 3) matrix Using Determinant and Co-factor
TLDRThis video tutorial explores the method of finding the inverse of a 3x2 matrix using the cofactor (co-actor) approach. The instructor begins by defining Matrix A and systematically calculates the cofactors for each element, adjusting for sign alternation across the matrix. The determinant of the submatrices is found, and these cofactors are used to create the adjugate matrix by transposing the cofactor matrix. The determinant of Matrix A is then calculated, and using this, the inverse of Matrix A is derived. The tutorial concludes with a practice exercise for the viewers, encouraging them to apply the cofactor method to another matrix and share their results.
Takeaways
- 📌 The script focuses on finding the inverse of a 3x2 matrix using the cofactor approach.
- 🔢 Matrix A is given with elements: [1 2; 1 -1; 2 1].
- 🌟 The cofactor matrix will have dimensions similar to the original matrix, and its elements are signed according to a specific pattern (positive, negative, positive, etc.).
- 📐 The first element of the cofactor matrix is calculated by eliminating the first row and column of Matrix A and finding the determinant of the remaining submatrix.
- 🔍 Each element of the cofactor matrix is determined by following the pattern of eliminating the appropriate row and column from Matrix A and calculating the determinant.
- ✅ The determinant of a submatrix is calculated by eliminating one row and one column and multiplying the remaining elements.
- 🌀 The sign of the determinant alternates, following the pattern of (-1)^(n+m) where n is the row number and m is the column number.
- 📝 The adjugate matrix (also called the adjoint matrix) of A is found by taking the transpose of the cofactor matrix.
- 🔢 The inverse of Matrix A is found by dividing 1 by the determinant of A and multiplying it by the adjugate matrix.
- 📊 An exercise is provided for the viewer to find the inverse of another matrix B with elements: [2 -3; 5 1; 6 0].
- 💡 The video aims to help viewers understand the process of finding the inverse of a matrix using the cofactor approach and encourages them to practice with the provided exercise.
Q & A
What is the main topic of the video script?
-The main topic of the video script is finding the inverse of a 3x2 matrix using the cofactor approach.
What is the first step in finding the inverse of a matrix?
-The first step in finding the inverse of a matrix is to solve for the cofactors of the matrix.
How does the sign pattern work for the cofactors in a 3x3 matrix?
-The sign pattern for the cofactors in a 3x3 matrix alternates as negative, positive, negative, positive, negative, positive.
What is the determinant of the 2x2 matrix formed by the first column of the given matrix?
-The determinant of the 2x2 matrix formed by the first column of the given matrix is -1 * (-2) - 1 * 2, which equals 0.
How is the cofactor matrix transposed to find the adjugate matrix?
-The adjugate matrix is found by transposing the cofactor matrix, which involves swapping the columns with the corresponding rows.
What is the determinant of the given matrix A?
-The determinant of the given matrix A is calculated by multiplying the elements on the main diagonal and subtracting the product of the elements on the other diagonal, resulting in 15.
How is the inverse of matrix A found?
-The inverse of matrix A is found by taking the adjugate matrix, dividing each element by the determinant of A, and then multiplying by the reciprocal of the determinant.
What is the final form of the inverse of matrix A?
-The final form of the inverse of matrix A is a 3x3 matrix with elements 0, 1/3, 1/5; 1/5, 2/3, 1/5; and 1/15, 0, 1/3.
What is the exercise given at the end of the video script?
-The exercise given at the end of the video script is to find the inverse of a given matrix B with elements 2, -3, 5; 6, 0, 1; and 15, -7, 2.
How can viewers share their solutions to the exercise?
-Viewers are encouraged to share their solutions to the exercise in the comment section of the video.
What is the significance of the cofactor approach in matrix operations?
-The cofactor approach is significant in matrix operations as it provides a method to calculate the inverse of a matrix, which is crucial for various mathematical and engineering applications.
Outlines
📌 Introduction to Finding the Inverse of a 3x2 Matrix
This paragraph introduces the process of finding the inverse of a 3x2 matrix using the Cauchy matrix approach. It begins by defining the given matrix A with elements 1, 2, 1, 2, -1, 2, 1, 1, -2 and explains the goal of finding its inverse, denoted as A^-1. The method involves solving for the cofactors of matrix A, emphasizing the importance of their signs which alternate in a specific pattern. The paragraph outlines the steps to calculate the cofactors by eliminating certain elements from the original matrix and computing the determinants of the resulting submatrices. It also highlights the dimension of the matrix and its relation to the dimensions of the cofactors.
🔢 Detailed Steps for Calculating Cofactors and Inverse
This paragraph delves into the detailed steps of calculating the cofactors and the inverse of matrix A. It explains how to eliminate elements from the original matrix to find the determinants that form the cofactors. The paragraph provides a step-by-step guide on how to compute the determinants for each cofactor, including the handling of signs and the resulting values. It then describes how to transpose the cofactors to find the adjugate matrix of A, which is essential for calculating the inverse. The paragraph concludes with the presentation of the final adjugate matrix and the method to find the inverse by dividing the adjugate matrix by the determinant of the original matrix.
📝 Exercise: Finding the Inverse of a Given Matrix
This paragraph concludes the video script by providing an exercise for the viewers to apply the learned method of finding the inverse of a matrix. It presents a new matrix B with elements 2, -3, 5, 6, 0, 1, and 15, and challenges the viewers to find its inverse using the cofactor approach. The paragraph encourages the viewers to share their solutions in the comment section, fostering engagement and interactive learning. It also recaps the process of finding the determinant of matrix A and its inverse, reinforcing the concepts and techniques discussed throughout the video script.
Mindmap
Keywords
💡inverse matrix
💡cofactor
💡matrix dimensions
💡determinant
💡adjugate matrix
💡transpose
💡linear equations
💡sign pattern
💡element elimination
💡matrix multiplication
Highlights
Introduction to finding the inverse of a 3x2 matrix using the cofactor approach.
Explanation of the matrix setup and identification of matrix A with its elements.
Detailed process on how to solve for the cofactor of matrix A, emphasizing the alternating sign rule for cofactors.
Computation of the cofactor for the first element in the matrix, showing the elimination process and determinant calculation.
Explanation of the process to compute the determinant of a reduced 2x2 matrix from matrix A.
Calculation and adjustment of signs for the second element's cofactor, resulting in a positive six.
Determination of the cofactor for the third position in matrix A with a resultant positive three.
Methodology for computing the cofactors of the second row of matrix A, highlighting determinant findings.
In-depth analysis of the determinant calculation for various matrix sub-sections, showcasing negative and positive adjustments.
Introduction of the adjoint matrix (adint of mat A), explaining the transformation from cofactors to the adjoint by transposing rows to columns.
Overview of calculating the inverse of matrix A by using the determinant and the adjoint matrix.
Explanation of determinant calculation for matrix A using the cofactor expansion method.
Comprehensive guide on transforming the determinant results into the final inverse matrix expression.
Summary of the mathematical processes and logic used throughout the calculation of the matrix inverse.
Closing remarks and an invitation to viewers to attempt solving for the inverse of a different matrix using the explained cofactor approach.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: