Simultaneous Equations with Three Unknowns

corbettmaths
31 Dec 201809:41
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a step-by-step guide on solving simultaneous equations with three unknowns, using a specific set of equations as an example. The presenter emphasizes the importance of clear working and methodical approach, recommending the use of different colors or annotations for clarity. The process involves eliminating one variable by combining two equations, resulting in two new equations with only two variables. These are then solved using standard methods, with the obtained values substituted back into one of the original equations to find the third variable. The presenter also suggests checking the solution by substituting the values into another equation to ensure accuracy.

Takeaways
  • 📚 Begin by familiarizing yourself with the basics of simultaneous equations and their solutions, especially if dealing with three unknowns.
  • 👀 Carefully set out your work to ensure clarity, which helps in avoiding mistakes and makes it easier to check your work later.
  • 🎨 Use different colors or labeling techniques to distinguish between different variables and steps in your working process.
  • 🚫 Always aim to eliminate one variable at a time; starting with 'z' in this case, makes the process more manageable.
  • 🔢 Double equations strategically to create terms that can be added or subtracted to eliminate variables.
  • 🔄 After eliminating 'z', you'll be left with two equations involving only 'x' and 'y', which simplifies the problem significantly.
  • 🔢 Use the two simplified equations to solve for one of the remaining variables, then substitute this value back into one of the original equations to find the last variable.
  • 🔍 Always check your solutions by substituting the found values back into the original equations to ensure their correctness.
  • 📈 The process can be summarized as: elimination of one variable, solving the resulting two-variable system, and checking the solution by substitution.
  • 📝 Annotation and clear labeling of your steps are crucial for understanding and for checking your work, especially in an exam setting.
  • 🎓 The video emphasizes the importance of carefulness with signs and following the steps to successfully solve simultaneous equations with three unknowns.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is solving simultaneous equations with three unknowns.

  • What is the first recommendation the speaker gives for solving these types of equations?

    -The first recommendation is to set out your work clearly, ensuring it's easy to understand and review for both the marker and yourself.

  • How many equations does the speaker initially have to work with?

    -The speaker initially has three equations to work with.

  • Which variable does the speaker choose to eliminate first and why?

    -The speaker chooses to eliminate the variable 'z' first because it can be nicely canceled out by doubling and adding or subtracting the equations.

  • What does the speaker do to eliminate 'z' from two of the equations?

    -The speaker doubles equation C and then adds it to equation A to eliminate 'z'.

  • What are the two new equations obtained after eliminating 'z'?

    -The two new equations obtained are 7x - 3y = 31 (equation D) and 7x - y = 29 (equation E).

  • How does the speaker solve for 'y' after obtaining equations D and E?

    -The speaker subtracts equation E from equation D to eliminate 'x', which results in -3y + y = 31 - 29, leading to y = -1.

  • What value does the speaker find for 'x' after substituting the value of 'y' into equation E?

    -After substituting y = -1 into equation E, the speaker finds that 7x = 28, leading to x = 4.

  • How does the speaker determine the value of 'z'?

    -The speaker substitutes the values of x and y into one of the original equations (equation A) and solves for 'z', finding that z = 2.

  • What does the speaker recommend after finding the values for 'x', 'y', and 'z'?

    -The speaker recommends checking the values by substituting them into one of the original equations, not one of the multiplied ones, to ensure the solution is correct.

  • How does the speaker emphasize the importance of careful work in solving these equations?

    -The speaker emphasizes the importance of being very careful with the signs and following the steps diligently to ensure correct results in exams or homework.

Outlines
00:00
📚 Introduction to Solving Simultaneous Equations with Three Unknowns

This paragraph introduces the topic of solving simultaneous equations with three unknowns, using a specific set of equations as an example. The speaker emphasizes the importance of setting out work clearly and recommends reviewing previous videos on related topics for better understanding. The process begins with the recommendation to annotate work thoroughly, possibly using different colored pens for clarity. The speaker then proceeds to explain the initial steps of solving the equations, focusing on eliminating one variable by combining two of the given equations. The chosen variables to solve for are x, y, and z, and the speaker illustrates how to cancel out the z variable by doubling equation C and adding it to equation A, resulting in a new equation D.

05:01
🔢 Substitution and Verification of Solutions

In this paragraph, the speaker continues the process of solving the simultaneous equations by using the newly formed equation D to find the value of y. By subtracting equation E from D, the speaker eliminates the x variable and solves for y, finding that y equals negative one. The speaker then substitutes the value of y into equation E to determine the value of x, which is found to be four. To ensure accuracy, the speaker recommends verifying the solutions by substituting the found values back into one of the original equations. The verification process confirms that the solutions are correct, with the values of x, y, and z being 4, -1, and 2, respectively. The speaker concludes by reiterating the importance of careful annotation and following a systematic approach to solving simultaneous equations with three unknowns.

Mindmap
Keywords
💡simultaneous equations
Simultaneous equations refer to a set of mathematical equations that are to be solved at the same time. In the video, the main theme revolves around solving such equations which involve three unknowns, x, y, and z. The process involves manipulating these equations to find the values of the variables that satisfy all the equations simultaneously. For example, the video provides a system of equations to solve: 3x + y - 2z = 7, x - 3y + 4z = 15, and 2x - 2y + z = 12.
💡unknowns
In the context of the video, unknowns are the variables x, y, and z that appear in the simultaneous equations. These are the values that the viewer is trying to determine. The term 'unknown' emphasizes that their values are not known initially but can be found through the process of solving the equations. The video demonstrates how to systematically find the values of these unknowns by setting up and solving a system of simultaneous equations.
💡variable elimination
Variable elimination is a technique used to solve systems of linear equations by adding or subtracting equations to eliminate one variable at a time. In the video, the presenter uses this method to eliminate the variable z from two of the equations by doubling one of the equations and adding it to another, thus simplifying the system and allowing for the solution of the remaining variables x and y.
💡annotating work
Annotating work refers to the process of labeling and explaining each step of a mathematical solution to ensure clarity and avoid mistakes. In the video, the presenter emphasizes the importance of annotating one's work when solving simultaneous equations with three unknowns, as it helps in tracking the steps taken and makes it easier to identify and correct any errors that might occur during the solution process.
💡test paper
A test paper is a document used in educational settings for assessing a student's understanding of a particular subject matter through a written examination. In the context of the video, the presenter mentions the use of a test paper as a platform for solving simultaneous equations, highlighting the need for clear and organized working, which is often required in exam settings.
💡corporate maps
Although not explicitly defined in the video, corporate maps likely refer to a method or tool used for visualizing and solving systems of equations, possibly through matrices or graphical representations. The presenter recommends reviewing videos on corporate maps for a better understanding of simultaneous equations, suggesting that it is a relevant technique in this mathematical context.
💡equations with tournaments
The term 'equations with tournaments' is not a standard mathematical term but seems to be used in the context of the video to refer to a specific method or set of techniques for solving simultaneous equations. The presenter suggests that viewers should review previous videos on this topic for a refresher, indicating that it is a significant part of the process being explained.
💡labeling
Labeling in the context of the video refers to the act of assigning labels (such as 'a', 'b', 'c', 'd', 'e') to the different equations in the system of simultaneous equations. This helps in organizing the equations and making the solution process more manageable and less prone to confusion. For instance, the video involves labeling the original equations and the derived equations (like 'equation d' and 'equation e') for easy reference.
💡substitution
Substitution is a mathematical technique used to solve a system of equations by replacing one variable with its equivalent value from another equation. In the video, after eliminating one variable (z), the presenter uses substitution to find the values of the remaining variables (x and y) by inserting the values obtained from the simplified equations back into one of the original equations.
💡checking solutions
Checking solutions involves verifying the values found for the variables by substituting them back into the original equations to ensure they satisfy all the equations simultaneously. The video emphasizes the importance of this step to confirm the correctness of the solutions obtained. For example, after finding the values for x, y, and z, the presenter checks the solution by substituting these values into one of the original equations (equation b) to confirm that it holds true.
💡algebra
Algebra is a branch of mathematics that uses symbols and rules of operations to solve equations. In the video, the process of solving simultaneous equations with three unknowns is an application of algebraic techniques. The presenter uses fundamental algebraic operations such as addition, subtraction, and the manipulation of equations to find the values of the variables, illustrating the practical use of algebra in problem-solving.
Highlights

The video introduces a method for solving simultaneous equations with three unknowns, using a specific set of equations as an example.

The importance of setting out work clearly when solving complex equations is emphasized for clarity and ease of error checking.

The strategy of canceling out one variable by combining two equations is recommended, starting with the variable 'z' in this case.

Equation 'C' is obtained by doubling Equation 'C' from the original set, which helps in canceling out 'z'.

Equation 'A' is also manipulated to facilitate the cancellation of 'z', resulting in Equation 'D'.

Two new equations, 'D' and 'E', with only 'x' and 'y' are formed after canceling out 'z', simplifying the problem.

The method of subtracting the equations to cancel out 'x' is described, leading to the solution for 'y'.

The value of 'y' is found to be -1 by solving the resulting simple equation after canceling 'x'.

Substituting the value of 'y' into one of the new equations ('E') allows for the calculation of 'x'.

The value of 'x' is determined to be 4 after substitution and simplification.

The original equations are used again, with the known values of 'x' and 'y', to solve for 'z'.

The value of 'z' is found to be 2 after substituting and simplifying the equation.

The video emphasizes the importance of checking the solution by substituting the values back into a different original equation to ensure accuracy.

The process is summarized as a systematic approach to solving simultaneous equations with three variables, highlighting the flexibility in choosing which variable to eliminate first.

The video concludes by encouraging careful attention to signs and steps, framing the topic as straightforward and manageable for exam situations.

Annotated work is showcased to aid understanding and demonstrate the process of solving the equations.

Transcripts

Browse More Related Video

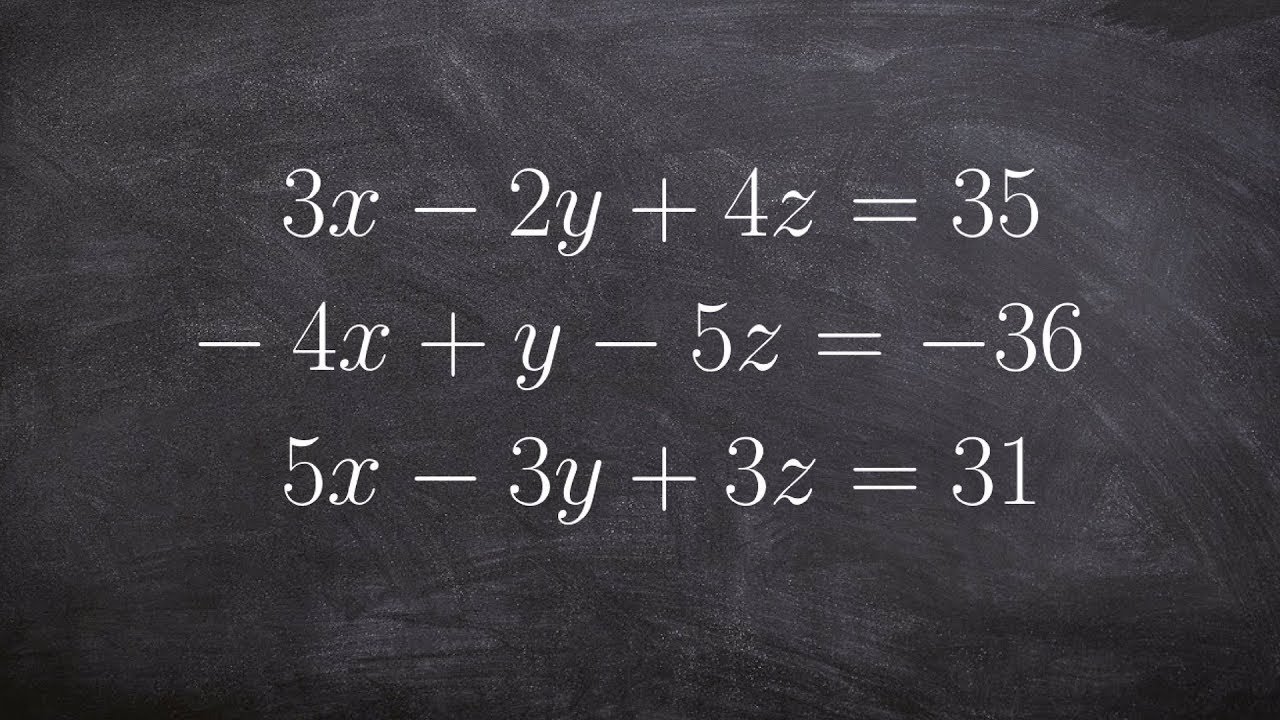
Solve a system with three variables

Solving 3 Equations for 3 Unknowns Using a Matrix in Row Echelon Form

Using Substitutions to Solve Equations (Precalculus - College Algebra 23)

7.3.1 Row Echelon Form of Linear Systems of Equations

7.1.3 Solving a System of Equations Using Elimination

7.1.1 Solving a System of Equations Using Substitution

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsSimultaneous EquationsThree UnknownsAlgebraEducationalTutorialClear ExplanationProblem SolvingChord MathVideo Guide