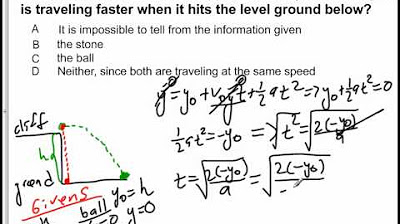
2015 AP Physics 1 free response 4
TLDRThe script explores the physics of two identical spheres released from the same height with different initial conditions. Sphere A falls straight down with no initial velocity, while Sphere B is given a horizontal velocity. Despite traveling different distances, both spheres reach the ground simultaneously due to the constant acceleration of gravity acting on them equally. The script explains this phenomenon through a free-body diagram and a graph of horizontal velocity components, highlighting that the horizontal motion does not affect the time of fall when air resistance is negligible.
Takeaways
- 📈 Two identical spheres are released from the same height with one having an initial horizontal velocity and the other having none.
- 🌐 Sphere A falls straight down with no initial horizontal velocity, while Sphere B is given a horizontal velocity and travels a distance D before landing.
- 🕒 Both spheres reach the ground at the same time despite Sphere B covering a greater distance.
- 🚫 Air resistance is considered negligible in this scenario.
- 🎨 A free-body diagram at time T sub F over two should show and label the forces exerted on each sphere, which are the same due to their identical mass and the force of gravity.
- 📊 For the horizontal components of velocity, Sphere A has zero horizontal velocity throughout its fall, while Sphere B maintains a constant horizontal velocity V sub zero until impact.
- 🔄 The spheres' horizontal velocities do not affect the time it takes for them to fall, as the force of gravity and the vertical distance are the same for both.
- 🛑 Sphere B's horizontal velocity remains constant until the moment of impact, at which point it becomes zero.
- 🤔 The key to understanding why both spheres hit the ground at the same time lies in recognizing that their vertical motions are identical, despite the difference in horizontal motion.
- 📐 The vertical acceleration due to gravity is uniform for both spheres, leading to their simultaneous impact even though they travel different paths.
- 🌟 The problem illustrates the principle of independent motion, where the horizontal and vertical components of motion can be analyzed separately to determine the outcome of a physical scenario.
Q & A
What is the initial condition of the spheres when released from the device?
-Both spheres are released from the same height H at time equals zero, with Sphere A having no initial velocity and falling straight down, while Sphere B is given an initial horizontal velocity of magnitude V_subzero.
What is the significance of the free-body diagram requested in the script?
-The free-body diagram is meant to illustrate and label the forces acting on each sphere at the moment they reach the ground (T_subF over two). Since air resistance is negligible, the only force acting on the spheres during their flight is gravity, which is identical for both spheres due to their identical mass.
How does Sphere A's horizontal velocity change over time?
-Sphere A does not have any horizontal velocity throughout its fall. It only experiences a vertical acceleration due to gravity, hence its horizontal velocity remains constant at zero.
What can be said about Sphere B's horizontal velocity during its flight?
-Sphere B maintains a constant horizontal velocity of magnitude V_subzero throughout its flight, as air resistance is negligible and no other forces act in the horizontal direction to change its speed.
How does the force of gravity affect the two spheres differently in the vertical direction?
-The force of gravity affects both spheres in the same way in the vertical direction. They both experience the same acceleration due to gravity, as they have the same mass and are subject to the same gravitational field.
Why do the spheres reach the ground at the same time despite traveling different distances?
-The spheres reach the ground at the same time because the horizontal motion of Sphere B does not affect the time it takes to fall vertically. Both spheres have the same vertical distance to cover and are accelerated at the same rate due to gravity, hence they fall at the same time.
What is the final horizontal velocity of Sphere B as it hits the ground?
-As Sphere B hits the ground, its horizontal velocity abruptly decreases to zero, as the force of impact and friction with the ground stops its horizontal motion instantaneously.
How does the velocity graph of Sphere A differ from that of Sphere B?
-The velocity graph of Sphere A is a horizontal line at zero, indicating no horizontal velocity change over time. In contrast, Sphere B's graph shows a constant horizontal velocity (V_subzero) until impact, at which point it drops to zero.
What would be the total velocity of Sphere B if you were to consider its horizontal and vertical components at the moment before impact?
-At the moment before impact, the total velocity of Sphere B would be the vector sum of its horizontal velocity (V_subzero) and its vertical velocity (which would be equal to Sphere A's vertical velocity at the same time of fall). However, the question does not provide information on Sphere B's vertical velocity, so a precise calculation cannot be made.
How does the trajectory of Sphere B differ from that of Sphere A?
-While Sphere A follows a straight vertical path due to the lack of horizontal velocity, Sphere B traces a parabolic trajectory because it has a constant horizontal velocity and an accelerating vertical velocity due to gravity.
What is the implication of the horizontal motion on the overall distance traveled by Sphere B?
-The horizontal motion implies that Sphere B travels a greater overall distance than Sphere A during its fall, due to the constant horizontal velocity component. However, this does not affect the time it takes for Sphere B to reach the ground, as the horizontal and vertical motions are independent in the context of their fall from the same height.
Outlines
🎥 Free-Fall Motion and Forces
This paragraph describes an experiment involving two identical spheres released from the same height with different initial conditions. Sphere A is released with no initial velocity, while Sphere B is given a horizontal velocity. Despite the differences in their paths and velocities, both spheres reach the ground at the same time due to the force of gravity acting on them. The only force acting on the spheres during their fall is gravity, which affects both spheres identically since they have the same mass. A free-body diagram is drawn to illustrate the force of gravity on each sphere at the moment they hit the ground.
📈 Velocity Components over Time
The paragraph focuses on the horizontal components of the velocities of the two spheres as a function of time. Sphere A, having no horizontal velocity, is represented by a flat line across the time axis. Sphere B, with an initial horizontal velocity V_sub_zero, maintains this velocity until it hits the ground. The graph illustrates that Sphere B's horizontal velocity remains constant throughout its flight, unaffected by gravity, which only influences the vertical motion. The final velocities of both spheres in the horizontal direction are also discussed, with Sphere B's velocity reducing to zero upon impact.
🧠 Understanding Simultaneous Impact
This section provides an explanation for why both spheres reach the ground at the same time despite traveling different distances. It emphasizes that the only force acting on the spheres during their descent is gravity, which affects both spheres equally due to their identical mass. Both spheres start with zero vertical velocity and are accelerated downward at the same rate, g, resulting in the same vertical velocity at any given time during their fall. The different horizontal velocities do not influence the time it takes for each sphere to cover the vertical distance, leading to their simultaneous impact with the ground. The paragraph also discusses the composition of Sphere B's velocity, which, while larger when considering both components, does not affect the time to cover the vertical distance.
Mindmap
Keywords
💡identical spheres
💡initial velocity
💡gravity
💡free-fall
💡horizontal distance
💡air resistance
💡free-body diagram
💡acceleration
💡velocity components
💡time of flight
💡force of gravity
Highlights
Two identical spheres are released from the same height at time equals zero.
Sphere A has no initial velocity and falls straight down.
Sphere B is given an initial horizontal velocity of magnitude V sub zero.
Both spheres reach the ground at the same time T sub F, despite sphere B covering more distance.
Air resistance is considered negligible in this scenario.
The only force acting on each sphere during flight is gravity.
The force of gravity is identical on both spheres due to their equal mass.
Sphere A has no horizontal velocity throughout its fall.
Sphere B maintains a constant horizontal velocity V sub zero until it hits the ground.
The horizontal component of velocity for sphere A remains zero, represented by a flat line on the graph.
The horizontal component of velocity for sphere B remains constant at V sub zero, represented by a horizontal line on the graph.
The spheres reach the ground at the same time because they are accelerated at the same rate in the vertical direction.
The vertical distance each sphere must cover is the same, hence they fall simultaneously.
Sphere B's horizontal velocity does not affect the time it takes to cover the vertical distance.
The sum of sphere B's velocity components results in a larger overall velocity, but not a greater vertical velocity.
In the vertical direction, both spheres cover the same distance in the same amount of time, resulting in simultaneous impact.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: