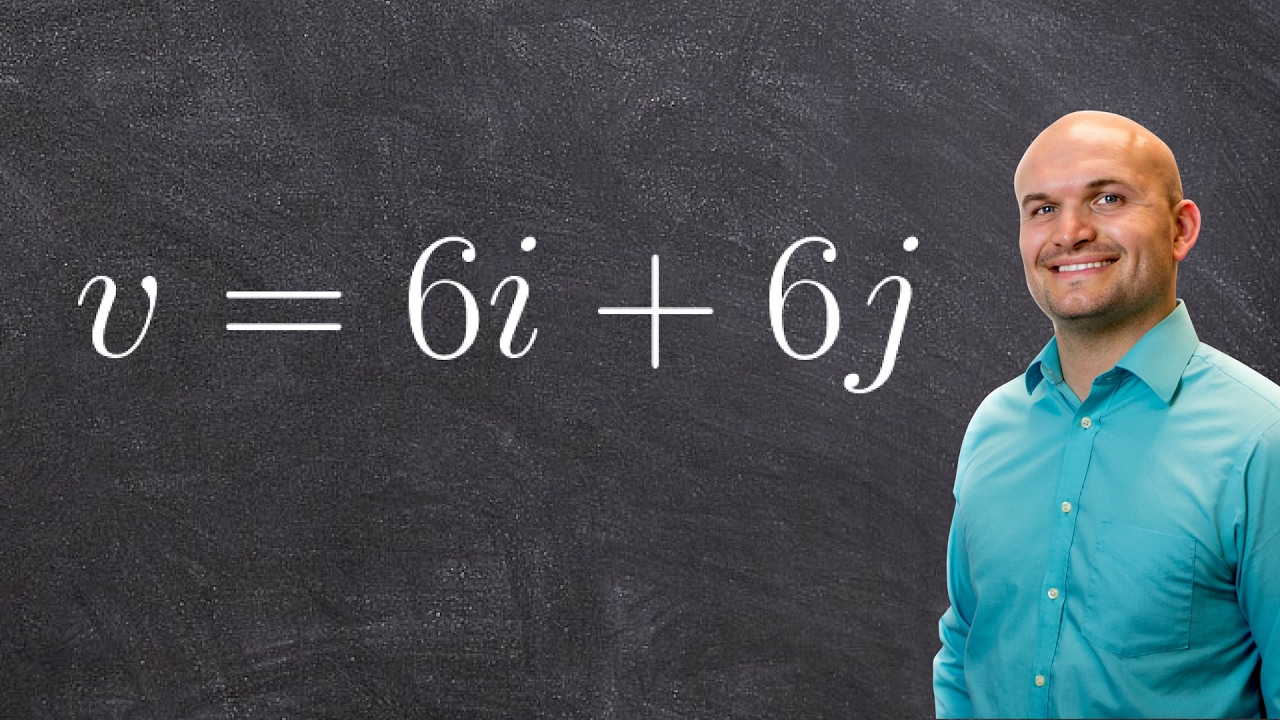01 - Calculating Magnitude of a Vector & Direction, Part 1 (Vector Magnitude & Angle)
TLDRThis lesson delves into vector calculations, focusing on determining a vector's magnitude and direction using its components. The instructor uses graphical examples to illustrate the process of calculating the magnitude and angle, emphasizing the application of the Pythagorean theorem and trigonometric functions. The importance of verifying the calculated angles against the vector's actual position is highlighted, with a detailed explanation of how to adjust angles obtained from the inverse tangent function to accurately reflect the vector's quadrant.
Takeaways
- 📐 Vectors can be described in two ways: by their components (x and y) or by their magnitude and direction (angle).
- 🔢 To find the magnitude of a vector given its components, apply the Pythagorean theorem: magnitude = √(Fx^2 + Fy^2).
- 📐 The angle (θ) of a vector relative to the positive x-axis can be found using the tangent function and the inverse tangent (arctangent).
- 📊 When working with the inverse tangent, always check the angle against the vector's quadrant to ensure the result makes sense geometrically.
- 🔄 For vectors in the second quadrant, a negative inverse tangent result indicates the angle is actually greater than 90 degrees and should be adjusted by adding 180 degrees.
- 📈 The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side, which is used to find the angle using the inverse tangent function.
- 🔎 When calculating vector angles, it's crucial to interpret the results correctly, especially when dealing with angles that span different quadrants.
- 🌟 The vector's direction is crucial in determining whether the calculated angle from the inverse tangent is correct or needs adjustment.
- 📚 Understanding the relationship between vector components and their magnitude and direction is fundamental for solving physics problems involving motion and forces.
- 🛠️ Practice is essential for mastering the calculation of vector magnitudes and angles, especially when dealing with different quadrants and the associated angle adjustments.
Q & A
What is the main topic of this physics lesson?
-The main topic of this physics lesson is calculating the vector magnitude and angle, and how to find these using the components of a vector.
What are the two ways to describe a vector?
-A vector can be described either in terms of its x and y components or in terms of its magnitude and direction.
How is the magnitude of a vector calculated using its components?
-The magnitude of a vector is calculated using the Pythagorean theorem, which states that the square root of the sum of the squares of its x and y components gives the length of the vector.
What is the significance of the Pythagorean theorem in vector calculations?
-The Pythagorean theorem is significant in vector calculations because it allows us to find the magnitude (or length) of a vector when we know its x and y components, by treating the components as sides of a right triangle.
How is the angle of a vector calculated from its components?
-The angle of a vector is calculated using the tangent function, specifically as the inverse tangent (arctangent) of the ratio of the y-component to the x-component.
Why is it important to check the calculated angle from the inverse tangent function?
-It is important to check the calculated angle because the inverse tangent function only gives an angle in the range from negative PI/2 to positive PI/2 (or -90 to 90 degrees). If the vector is in a different quadrant, the angle may need to be adjusted by adding or subtracting 180 degrees to match the actual direction of the vector.
What happens when the components of a vector have different signs?
-When the components of a vector have different signs, it indicates that the vector is in a different quadrant, and the calculated angle from the inverse tangent function may need to be adjusted by adding 180 degrees to accurately represent the vector's direction.
How can you verify if the calculated angle for a vector is correct?
-You can verify if the calculated angle is correct by comparing it with the expected direction of the vector based on its components. If the calculated angle does not match the expected direction, you may need to adjust it by adding or subtracting 180 degrees.
What is the relationship between the angle inside a right triangle formed by vector components and the angle calculated from the inverse tangent function?
-The angle inside the right triangle formed by vector components is complementary to the angle calculated from the inverse tangent function. If the inverse tangent gives an angle of 45 degrees, the angle inside the triangle is 90 - 45 = 45 degrees.
In the context of this lesson, what is the significance of the quadrant in which a vector lies?
-The quadrant in which a vector lies is significant because it affects the direction of the angle measured from the positive x-axis. Different quadrants require different adjustments to the angle calculated by the inverse tangent function to correctly represent the vector's direction.
How can you find the components of a vector if you are given its magnitude and angle?
-If you are given the magnitude and angle of a vector, you can find its components by using trigonometric functions. The x-component is found by multiplying the magnitude with the cosine of the angle, and the y-component is found by multiplying the magnitude with the sine of the angle.
Outlines
📚 Introduction to Vector Magnitude and Angle Calculation
This paragraph introduces the concept of calculating the vector magnitude and angle, emphasizing the importance of understanding vectors in physics. The lesson plan is outlined, highlighting that the current lesson focuses on calculating magnitude and angle from given components, with future lessons covering vector addition through components and introduction to motion and acceleration. The significance of vectors in solving motion problems is stressed, and a brief review of previous lessons is provided, setting the stage for the detailed explanation of how to calculate the magnitude and angle of a vector using its components.
🔢 Calculating Magnitude and Angle from Components
The paragraph delves into the process of calculating the magnitude and angle of a vector from its x and y components. A step-by-step explanation is given, starting with a graphical example and progressing to the mathematical application of the Pythagorean theorem to find the magnitude. The concept of breaking a vector into components is reiterated, and the calculation is demonstrated using specific values for F sub X and F sub Y. The paragraph also explains how to find the angle using the tangent function and the inverse tangent, providing a clear method for determining both the magnitude and direction of a vector.
📐 Quadrant-Specific Vector Analysis
This section focuses on analyzing vectors in different quadrants, emphasizing the need to be cautious when calculating the angle. The example given involves a vector in the second quadrant, with a negative x component and a positive y component. The calculation of the magnitude using the Pythagorean theorem is repeated, resulting in a different magnitude. The paragraph then discusses the process of finding the angle using the tangent function and inverse tangent, highlighting the importance of verifying the calculated angle against the vector's position in the quadrant. The concept of adjusting the angle by adding 180 degrees when necessary is introduced, ensuring that the angle aligns with the vector's actual direction.
🔄 Understanding Inverse Tangent and Angle Adjustment
The paragraph further explores the use of the inverse tangent function in calculating vector angles and the potential for ambiguous results. It explains that the calculator's inverse tangent function assumes the vector is in a specific quadrant, which may not always be the case. The concept of adding 180 degrees to the angle to correct its direction is elaborated, ensuring that the angle is consistent with the vector's actual position. The paragraph also provides a clear example of how to adjust the angle from negative 45 degrees to 135 degrees by adding 180 degrees, reinforcing the importance of this adjustment for accurate vector analysis.
📌 Final Thoughts on Vector Analysis
In the concluding paragraph, the speaker reiterates the importance of understanding the inverse tangent function and its limitations when calculating vector angles. The paragraph emphasizes the need to verify the calculated angle against the vector's position and to adjust the angle as necessary. The concept of the calculator's programmed limitation is discussed, explaining why the inverse tangent may give an angle that seems incorrect without adjustment. The speaker encourages the audience to follow through to the next section for further examples and clarification on calculating vector magnitude and angle in all quadrants.
Mindmap
Keywords
💡Vector
💡Magnitude
💡Angle
💡Components
💡Pythagorean Theorem
💡Tangent Function
💡Inverse Tangent
💡Quadrants
💡Trigonometry
💡Force
💡Physics Concepts
Highlights
Lesson focuses on calculating vector magnitude and angle.
Vector components can be used to determine the magnitude and direction of a vector.
The Pythagorean theorem is applied to find the magnitude of a vector.
The tangent function is used to find the angle of a vector from the positive x-axis.
The angle calculated from the inverse tangent function needs to be verified against the vector's actual position.
A negative angle from the inverse tangent function indicates the vector is in the opposite quadrant.
The magnitude of a vector is always positive and can be found using the Pythagorean theorem regardless of the vector's direction.
The angle of a vector can be 180 degrees off from the inverse tangent function's result if the vector is in a different quadrant.
The process of calculating vector magnitude and angle is applicable to various physics and motion problems.
The components of a vector form a right triangle, allowing for the application of trigonometric functions.
The graphical representation of vectors helps in understanding the calculation of magnitude and angle.
The lesson introduces the concept of vector addition using components, which is a fundamental concept in physics.
The importance of verifying the results of the inverse tangent function is emphasized to ensure the accuracy of vector angle calculations.
The lesson provides a step-by-step approach to vector calculations, emphasizing the importance of each step.
The practical application of vector calculations is demonstrated through the use of force vectors.
The lesson sets the stage for further exploration of motion and acceleration in one dimension, emphasizing the role of vectors.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: