A Brief Look at the Force of Drag using Numerical Modeling (or The Euler Method)

Flipping Physics

9 May 201421:59

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Mr. P introduces the concept of numerical modeling, specifically the Euler method, to account for air resistance in projectile motion. The lesson delves into the conditions for projectile motion, the impact of drag on an object's trajectory, and the calculations involved in determining the force of drag. Utilizing a spreadsheet, the video demonstrates how to calculate the effects of drag on a Lacrosse ball, concluding that air resistance decreases the horizontal displacement by approximately nine millimeters, validating the initial statement.

Takeaways

📚 Numerical modeling, specifically the Euler method, is a technique used to solve ordinary differential equations and can be applied to include the force of drag in projectile motion calculations.
🌬️ Air resistance significantly impacts projectile motion, altering the object's acceleration and velocity, thus affecting its trajectory.
🎾 The conditions for an object to be in projectile motion include traveling through the air in two dimensions and initially ignoring air resistance.
📐 The force of drag is calculated using the formula: Drag = 1/2 * ρ * V² * D * A, where ρ is the density of the medium, V is the velocity, D is the drag coefficient, and A is the cross-sectional area of the object.
🏓 The drag coefficient (D) for a smooth sphere, like a Lacrosse ball, is approximately 0.5 according to NASA.
📊 The density of air at sea level and 15 degrees Celsius is approximately 1.275 kg/m³, which is crucial for calculating the force of drag.
📈 The Euler method involves breaking down the motion into small time intervals and assuming constant acceleration within each interval to simplify the calculations.
🔢 Excel can be used to perform complex calculations related to the motion of objects, including handling the iterative nature of the Euler method efficiently.
📌 The initial velocity conversion from miles per hour to meters per second is necessary for consistent units in calculations.
🌐 The actual displacement of an object in the x-direction with air resistance is slightly less than the ideal displacement without air resistance.
🔄 The process of updating the position and velocity at each small time step allows for the simulation of the object's motion while accounting for the changing forces acting on it.

Q & A

What is the main topic of discussion in the transcript?
-The main topic of discussion is the inclusion of air resistance in projectile motion calculations using numerical modeling, specifically the Euler method.
Who is Mr. P and what is his role in the transcript?
-Mr. P is a teacher or presenter who is leading the discussion on projectile motion and numerical modeling, providing explanations and guiding the students through the concepts.
What is the Euler method?
-The Euler method is a numerical technique used for solving ordinary differential equations. It is applied here to model the motion of an object considering air resistance.
What are the conditions for an object to be in projectile motion according to the transcript?
-For an object to be in projectile motion, it must be flying through the air in two dimensions and air resistance must be ignored.
How does air resistance affect the motion of an object?
-Air resistance decreases the displacement in the x-direction of the object and changes the acceleration in the y-direction, making it no longer constant negative 9.81 meters per second squared.
What is the typical equation for the force of drag?
-The typical equation for the force of drag is F_drag = 0.5 * ρ * V^2 * C_d * A, where ρ is the density of the medium, V is the velocity of the object, C_d is the drag coefficient, and A is the cross-sectional area of the object.
What is the drag coefficient for a smooth sphere according to NASA?
-According to NASA, the drag coefficient for a smooth sphere is about 0.5.
How does the density of air affect the drag force?
-The density of air affects the drag force as it is a part of the force of drag equation. A higher density of air results in a greater drag force acting on the object.
What is the significance of using Excel in this context?
-Excel is used to perform the numerous calculations involved in numerical modeling efficiently. It allows for the easy manipulation of data and the application of formulas to model the motion of the object over time.
How does the velocity of the object change due to drag force?
-The velocity of the object changes as the drag force, which depends on the velocity, alters the net force and consequently the acceleration of the object. This results in a non-uniformly accelerated motion.
What was the calculated difference in displacement caused by air resistance?
-The calculated difference in displacement caused by air resistance was 0.00859 meters, which is approximately nine millimeters or just less than one centimeter.

Outlines

00:00

📚 Introduction to Projectile Motion and Numerical Modeling

The first paragraph introduces the concept of projectile motion and the impact of air resistance on it. Mr. P explains that while air resistance is typically neglected in calculations, it does affect the horizontal displacement of a ball. The Euler method, a numerical modeling technique, is introduced as a way to incorporate air resistance into the calculations. The historical context of Leonhard Euler and his method for solving ordinary differential equations is provided. The conditions for an object to be in projectile motion are discussed, emphasizing the need to ignore air resistance. The paragraph concludes with a discussion on the forces acting on the ball and the typical equation for the force of drag.

05:00

📈 Density, Velocity, and Drag Force Calculations

This paragraph delves into the specifics of calculating the drag force on the ball, considering the density of air and the velocity of the object. The density of air at sea level and 15 degrees Celsius is used, and the velocity's dependency on the drag force is discussed. The concept of uniformly accelerated motion (UAM) is clarified, and the Euler method's approach of breaking the motion into short parts with constant acceleration is explained. The paragraph highlights the complexity of these calculations and introduces the use of Excel for simplification.

10:03

🔢 Deriving Equations for Acceleration and Position

The focus of this paragraph is on deriving the equations for acceleration, final velocity, and final position in the x-direction. The net force in the x-direction is calculated, and the acceleration is determined using the drag force equation. The initial velocity in the x-direction is converted from miles per hour to meters per second. The acceleration in the x-direction is calculated, and the final velocity and position after 1/100th of a second are determined using the UAM equations. The process is explained step by step, with an emphasis on the importance of each calculation.

15:03

📊 Excel Modeling for Numerical Analysis

This paragraph demonstrates the practical application of Excel for numerical modeling. The Lacrosse ball's specifications, such as weight, mass, and drag coefficient, are input into the spreadsheet. The equations for the x-direction are set up in Excel, with explanations on absolute and relative references. The process is then repeated for the y-direction, taking into account the differences in drag force and gravity. The paragraph emphasizes the efficiency of using Excel for complex calculations and the potential for further analysis and adjustments to the model.

20:05

🎯 Comparing Ideal and Actual Displacement with Drag

The final paragraph synthesizes the information and calculations from the previous sections to compare the ideal and actual displacement of the ball in the x-direction when air resistance is considered. The velocity changes over time due to the drag force are analyzed, and the resulting displacements are calculated. The difference caused by air resistance is quantified, confirming Mr. P's earlier statement that air resistance decreases the horizontal displacement by less than a centimeter. The Excel file used in the video is mentioned as a resource for further exploration of the topic.

Mindmap

Keywords

💡Projectile Motion

Projectile motion is a type of motion where an object is launched into the air and moves under the influence of gravity alone, typically in a two-dimensional path. In the video, the concept is initially discussed in the context of neglecting air resistance but later, the inclusion of air resistance through numerical modeling is explored to understand its effect on the motion.

💡Air Resistance

Air resistance is the force that opposes the motion of an object through the air. It is a type of drag force that increases as the object's velocity increases. In the context of the video, air resistance is a crucial factor that needs to be considered when calculating the motion of a ball in real-world scenarios, as it affects the ball's displacement and velocity.

💡Euler Method

The Euler method, also known as numerical modeling, is a technique used to solve ordinary differential equations with discrete calculations. It approximates the solution of a system by breaking it down into small time steps and calculating the state variables at each step. In the video, the Euler method is used to model the motion of a ball including the effects of air resistance.

💡Drag Coefficient

The drag coefficient is a dimensionless number that is used in fluid dynamics to quantify the drag force on an object in a fluid, such as air. It depends on the shape, size, and surface properties of the object. In the video, the drag coefficient is a key parameter used in the calculations to model the force of air resistance on the ball.

💡Cross-Sectional Area

The cross-sectional area of an object is the area that is perpendicular to the direction of motion, through which the object is traveling. It is important in calculating the force of drag as it directly influences the magnitude of the drag force. In the context of the video, the cross-sectional area of the ball is used to determine the force of drag acting on it.

💡Density of Air

The density of air is a measure of mass per unit volume of air. It varies with altitude, temperature, and pressure, and plays a significant role in determining the magnitude of the drag force on an object moving through the air. In the video, the density of air at sea level and a specific temperature is used to calculate the drag force acting on the ball.

💡Acceleration

Acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that describes how quickly an object speeds up, slows down, or changes direction. In the video, the concept of acceleration is central to understanding how air resistance affects the motion of the ball, as it leads to changes in the ball's velocity and position.

💡Uniformly Accelerated Motion (UAM)

Uniformly accelerated motion is a type of motion in which an object's acceleration is constant. This means that the object's velocity changes by equal amounts in equal intervals of time. In the video, the motion of the ball is not uniformly accelerated due to the changing drag force, but the Euler method allows for the approximation of constant acceleration over very short time intervals.

💡Excel

Excel is a spreadsheet application developed by Microsoft that allows users to organize, format, and calculate data using formulas and functions. In the video, Excel is used as a tool to perform the complex calculations required for numerical modeling and to implement the Euler method for the ball's motion.

💡Free Body Diagram

A free body diagram is a graphical representation that shows all the forces acting on an object. It helps in visualizing and analyzing the physical situation to determine the motion of the object. In the video, a free body diagram is drawn to identify and calculate the forces acting on the ball, such as gravity and drag.

💡Circumference

Circumference is the linear distance around the edge of a circle or circular object. It is an important parameter for calculating the cross-sectional area and the drag force acting on a spherical object like a ball. In the video, the circumference of the Lacrosse ball is used to determine its radius and subsequently its cross-sectional area.

Highlights

Numerical modeling, specifically the Euler method, is introduced as a way to include air resistance in projectile motion calculations.

The Euler method was devised by 18th-century mathematician Leonhard Euler for solving ordinary differential equations.

Air resistance decreases the displacement in the x-direction of a ball by less than 1 centimeter, according to Mr. P's previous statement.

Projectile motion traditionally ignores air resistance, assuming constant acceleration in the y-direction (9.81 m/s^2) and constant velocity in the x-direction.

The force of drag is calculated using the equation Fdrag = 1/2 * ρ * V^2 * D * A, where ρ is the density of the medium, V is the velocity, D is the drag coefficient, and A is the cross-sectional area.

The drag coefficient (D) for a smooth sphere, such as a Lacrosse ball, is approximately 0.5 according to NASA.

The density of air at sea level and 15 degrees Celsius is approximately 1.275 kg/m^3.

The Lacrosse ball's radius is calculated to be about 0.031835 meters based on its given circumference and weight.

The Euler method breaks down motion into very short parts where the acceleration can be assumed constant, allowing for the use of uniformly accelerated motion (UAM) equations.

Excel is used to harness the power of numerical modeling by automating the repetitive calculations required for the Euler method.

The initial velocity in the x-direction is converted from 10.0 miles per hour to 4.4694444 meters per second.

The acceleration in the x-direction is calculated to be -0.13953 meters per second squared.

The final velocity in the x-direction after 1/100th of a second is 4.46805 meters per second, showing a decrease due to drag.

The final position in the x-direction after 1/100th of a second is 0.04469 meters, demonstrating the effect of drag on displacement.

The acceleration in the y-direction starts at -9.81 m/s^2 but is not constant due to the changing velocity and drag force in the y-direction.

The Euler method allows for the calculation of the ball's motion with air resistance, proving that the displacement difference due to drag is approximately 9 millimeters.

The Excel file used for the numerical modeling is made available on Mr. P's website for further exploration and modification.

Transcripts

Browse More Related Video

(Part 1 of 2) An Introductory Projectile Motion Problem with an Initial Horizontal Velocity

AP Physics 1 - Air Resistance

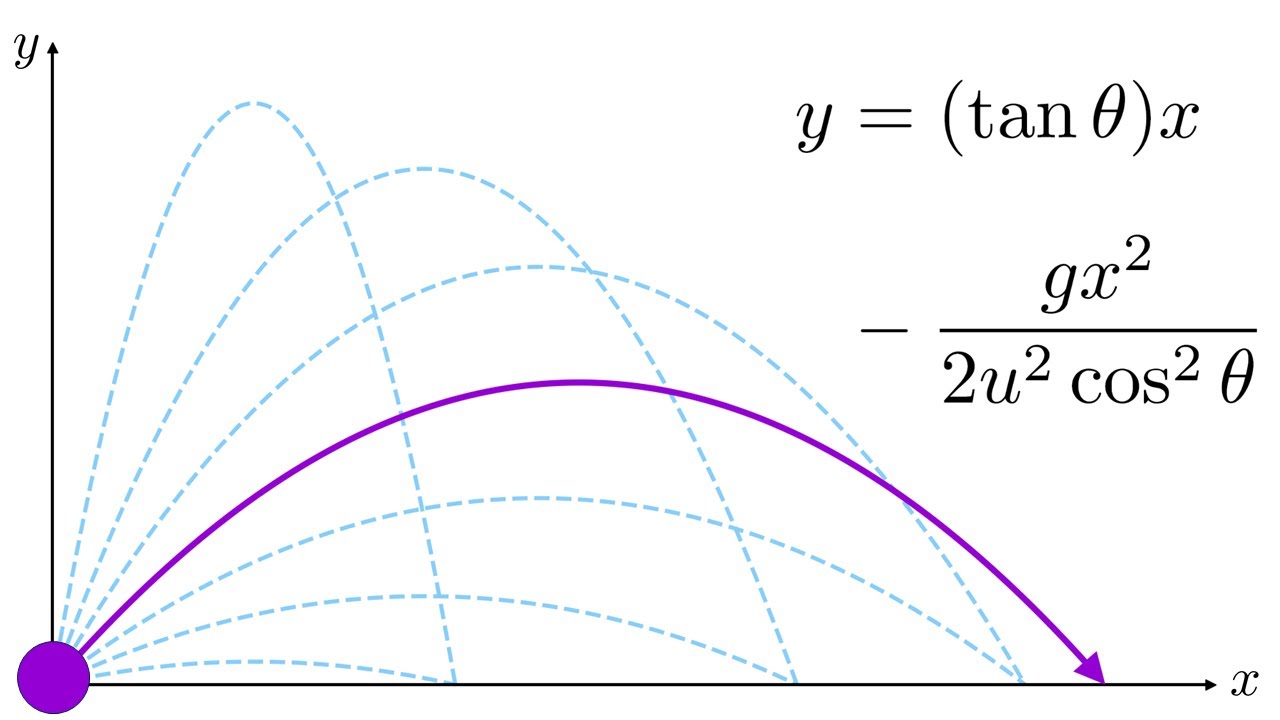
Trajectory of a projectile without drag

College Physics 1: Lecture 12 - Projectile Motion

College Physics 1: Lecture 18 - Friction and Drag

Nerd-A-Pult - An Introductory Projectile Motion Problem

Related Tags

Projectile Motion Drag Force Numerical Modeling Euler Method Physics Education Excel Application Lacrosse Ball Air Resistance Force Analysis Acceleration Calculation