AP Physics 1 - Rotational Kinetic Energy

Dan Fullerton
21 Mar 201309:02
EducationalLearning
32 Likes 10 Comments

TLDRIn this lesson, Dan Fullerton explores rotational kinetic energy, drawing parallels with translational kinetic energy. He explains how to calculate the kinetic energy of rotating objects using the formula one-half the moment of inertia times the square of the angular velocity. The lesson uses examples like a spinning basketball and an ice skater to illustrate concepts, and concludes with a problem involving a bowling ball to demonstrate the application of these principles. The key takeaway is understanding the relationship between moment of inertia, angular velocity, and rotational kinetic energy in various scenarios.

Takeaways
  • ๐ŸŒŸ Kinetic energy has two forms: translational (due to linear motion) and rotational (due to spinning or rotation).
  • ๐Ÿ“ The formula for translational kinetic energy is KE_trans = 1/2 * m * v^2, where m is mass and v is velocity.
  • ๐Ÿ”„ The formula for rotational kinetic energy is KE_rot = 1/2 * I * ฯ‰^2, where I is the moment of inertia and ฯ‰ is the angular velocity.
  • ๐Ÿคธโ€โ™€๏ธ Analogous relationships exist between linear and rotational motion, such as displacement (s = R * ฮธ), velocity (v = R * ฯ‰), and acceleration (a = R * ฮฑ).
  • ๐Ÿ€ The basketball example demonstrates how to calculate both translational and rotational kinetic energy, with the basketball having a total kinetic energy of approximately 20.6 joules.
  • โšฝ๏ธ For the soccer ball example, the moment of inertia is approximated using the formula for a hollow sphere (I = 2/3 * m * r^2).
  • ๐Ÿ’ƒ The ice skater example illustrates how reducing the moment of inertia (by pulling arms and legs in) results in an increase in angular velocity, and consequently, a doubling of the rotational kinetic energy.
  • ๐ŸŒ๏ธโ€โ™€๏ธ The ice skater's increased rotational kinetic energy is due to the conservation of angular momentum; when the skater pulls in her arms and legs, she does work that adds to her rotational kinetic energy.
  • ๐ŸŽณ The bowling ball example shows how to find the rotational kinetic energy, assuming it rolls without slipping, using the moment of inertia formula for a solid sphere (I = 2/5 * m * r^2).
  • ๐Ÿ”ข The total kinetic energy of the bowling ball is the sum of its translational and rotational kinetic energies, calculated to be approximately 176 joules.
  • ๐Ÿ“š Understanding rotational kinetic energy is crucial for analyzing and solving problems involving rotating objects in physics.
Q & A

  • What is the main topic of the lesson?

    -The main topic of the lesson is rotational kinetic energy.

  • How is translational kinetic energy calculated?

    -Translational kinetic energy is calculated using the formula 1/2 * mass * (velocity)^2.

  • What is the formula for rotational kinetic energy?

    -The formula for rotational kinetic energy is 1/2 * moment of inertia * (angular velocity)^2.

  • What is the relationship between linear and angular kinetic energy formulas?

    -Both formulas have a similar structure, with 1/2 multiplied by the respective inertia (mass for linear and moment of inertia for angular) and the square of the velocity (either linear or angular).

  • How does the basketball's moment of inertia relate to its mass and radius if it is approximated as a hollow sphere?

    -For a hollow sphere, the moment of inertia is 2/3 * mass * (radius)^2.

  • What is the total kinetic energy of the basketball with a mass of 0.62 kg, traveling at 8 m/s, and spinning at 5 radians per second?

    -The total kinetic energy is the sum of its translational kinetic energy (19.84 joules) and its rotational kinetic energy (0.75 joules), which is approximately 20.6 joules.

  • What happens to an ice skater's angular velocity when she brings her arms and legs closer to her body?

    -When the ice skater brings her arms and legs closer to her body, her moment of inertia decreases. Since angular momentum remains constant, her angular velocity increases.

  • How does the rotational kinetic energy change when the ice skater's moment of inertia is reduced by half?

    -When the moment of inertia is reduced by half and angular momentum remains constant, the rotational kinetic energy doubles because the angular velocity increases by a factor of two, and it is squared in the kinetic energy formula.

  • What is the moment of inertia of a solid sphere?

    -The moment of inertia of a solid sphere is given by the formula 2/5 * mass * (radius)^2.

  • Assuming a bowling ball rolls down a lane without slipping, how can you find its angular velocity?

    -The angular velocity of the bowling ball can be found by dividing its linear velocity by its radius (Omega = V/R).

  • What is the total kinetic energy of a 7 kg bowling ball with a radius of 10.9 cm, traveling at 6 m/s?

    -The total kinetic energy of the bowling ball is the sum of its translational kinetic energy (1/2 * 7 kg * (6 m/s)^2) and its rotational kinetic energy (1/2 * 0.033 kg m^2 * (55 rad/s)^2), which is approximately 176 joules.

Outlines
00:00
๐Ÿ“š Introduction to Rotational Kinetic Energy

This paragraph introduces the concept of rotational kinetic energy, comparing it with translational kinetic energy. It explains how to calculate the kinetic energy of a rotating object by discussing the types of kinetic energy and their formulas. The key points include the definition of translational and rotational kinetic energy, the relationship between mass, velocity, moment of inertia, and angular velocity, and the analogy between linear and rotational motion. The paragraph also provides an example of a basketball flying through the air, calculating both its translational and rotational kinetic energy to demonstrate the application of these concepts.

05:01
๐Ÿ’ƒ Ice Skater and Rotational Kinetic Energy

This paragraph explores the application of rotational kinetic energy in the context of an ice skater. It explains how the skater's angular velocity and rotational kinetic energy change when she brings her arms and legs closer to her body, thereby reducing her moment of inertia. The paragraph highlights the conservation of angular momentum and how it affects the skater's rotational velocity. It also discusses the work done by the skater and how it translates into increased rotational kinetic energy. Another example is given, where a bowling ball's rotational kinetic energy is calculated, assuming it does not slip while rolling down a lane.

Mindmap
Keywords
๐Ÿ’กRotational Kinetic Energy
Rotational kinetic energy refers to the energy of motion associated with an object's rotation. It is quantified by the formula one-half the product of the moment of inertia (I) and the square of the angular velocity (Omega). In the video, this concept is used to calculate the energy possessed by a rotating basketball and a bowling ball, emphasizing its importance in understanding their motion and dynamics.
๐Ÿ’กMoment of Inertia
The moment of inertia (I) is a measure of an object's resistance to rotational motion about a particular axis. It depends on both the mass of the object and how that mass is distributed relative to the axis of rotation. In the context of the video, the moment of inertia is crucial for calculating rotational kinetic energy and is derived for a hollow sphere and a solid sphere to analyze the basketball's and bowling ball's rotation, respectively.
๐Ÿ’กAngular Velocity
Angular velocity (Omega) is the rate at which an object rotates around a specific axis. It is measured in radians per second and is a fundamental component in the calculation of rotational kinetic energy. The video illustrates the concept by using the angular velocity of a spinning basketball and a rolling bowling ball to determine their rotational kinetic energies.
๐Ÿ’กTranslational Kinetic Energy
Translational kinetic energy is the energy of motion associated with an object moving in a straight line. It is calculated using the formula one-half the product of the object's mass (M) and the square of its velocity (V). In the video, translational kinetic energy is contrasted with rotational kinetic energy to highlight the different types of energy involved in an object's motion.
๐Ÿ’กAnalogues
In the context of the video, analogues refer to the parallels drawn between rotational and translational motion. The video explains how concepts like displacement, velocity, acceleration, and kinetic energy have analogous counterparts in both rotational and translational dynamics, such as angular displacement, angular velocity, and angular acceleration.
๐Ÿ’กIce Skater
The ice skater example in the video is used to illustrate the conservation of angular momentum and its implications on rotational kinetic energy. When the skater brings their arms and legs closer to their body, they reduce their moment of inertia, which in turn increases their angular velocity while keeping the angular momentum constant.
๐Ÿ’กBowling Ball
The bowling ball serves as an example in the video to demonstrate the calculation of rotational kinetic energy for a solid sphere. The ball's mass and radius are used to determine its moment of inertia and subsequently its rotational kinetic energy when rolling down a lane.
๐Ÿ’กWork
In the context of the video, work refers to the energy transfer that occurs when a force is applied over a distance. The skater's work in pulling their arms and legs in results in an increase in rotational kinetic energy, as the extra energy is converted into increased rotational motion.
๐Ÿ’กSolid Sphere
A solid sphere is a three-dimensional object with a uniform density throughout. In the video, the bowling ball is approximated as a solid sphere for the purpose of calculating its moment of inertia, which is different from that of a hollow sphere.
๐Ÿ’กHollow Sphere
A hollow sphere is a spherical object with an empty interior. In the video, the basketball is approximated as a hollow sphere to calculate its moment of inertia. This approximation is used to analyze the basketball's rotation and to determine its rotational kinetic energy.
Highlights

The lesson focuses on rotational kinetic energy and its calculation.

Kinetic energy of a rotating object is calculated using the formula one-half the moment of inertia times the square of the angular velocity.

There are parallels between translational and rotational kinetic energy, such as one-half mass compared to rotational inertia and linear speed squared to angular speed squared.

Analogs exist for various physical quantities in both translational and rotational contexts, such as displacement, velocity, acceleration, and time.

Newton's second law and the concept of net force and torque are applicable to both translational and rotational scenarios.

Linear momentum is given by the product of mass and velocity (P = mV), while angular momentum is the product of moment of inertia and angular velocity (L = Iฮฉ).

The basketball example demonstrates the calculation of both translational and rotational kinetic energy.

The moment of inertia for a hollow sphere is calculated as two-thirds the mass times the square of its radius.

The ice skater problem illustrates how a change in the moment of inertia affects angular velocity and rotational kinetic energy.

When the skater pulls her arms and legs in, her rotational kinetic energy doubles due to the decrease in moment of inertia and the increase in angular velocity.

The bowling ball example shows how to find the rotational kinetic energy assuming it does not slip.

The moment of inertia for a solid sphere is calculated as two-fifths the mass times the square of its radius.

The bowling ball's total kinetic energy is the sum of its translational and rotational kinetic energies.

Understanding rotational kinetic energy is crucial for applications in physics and engineering, such as in the analysis of spinning objects and machinery.

The lesson provides a comprehensive introduction to rotational kinetic energy, its theoretical foundations, and its practical applications.

For further information and assistance, resources such as eight plus physics com are recommended.

The lesson emphasizes the importance of understanding the relationship between rotational and translational kinetic energy for a deeper comprehension of motion and dynamics.

Transcripts

Browse More Related Video

Moment of Inertia Introduction and Rotational Kinetic Energy Derivation

Rotational kinetic energy | Moments, torque, and angular momentum | Physics | Khan Academy

Rotational Energy | Physics with Professor Matt Anderson | M12-17

AP Physics 1 - Rotational Dynamics

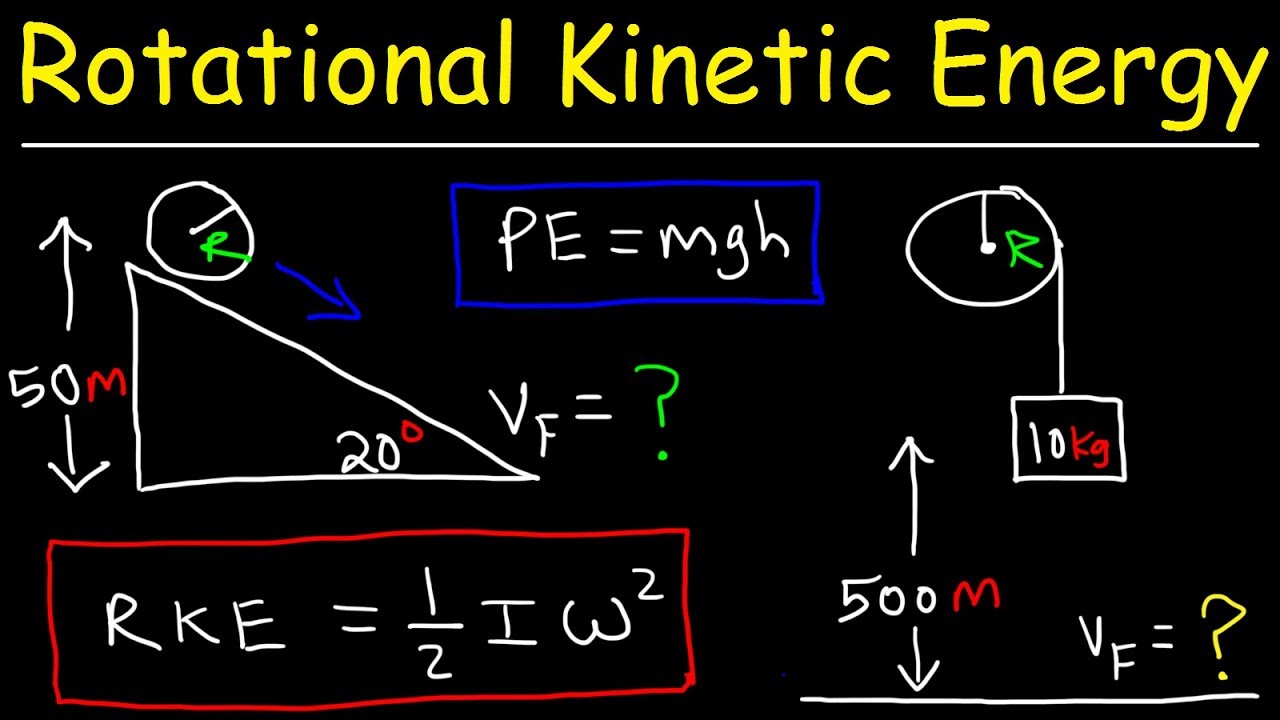
Rotational Kinetic Energy and Moment of Inertia Examples & Physics Problems

8.01x - Lect 19 - Rotating Objects, Moment of Inertia, Rotational KE, Neutron Stars

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EducationKinetic EnergyRotational DynamicsSports ScienceMechanicsClassroom LessonEnergy CalculationMomentum ConservationSkating TechniquesBowling Motion