High School Physics - Power
TLDRIn this informative video, Mr. Fullerton explains the concept of power, defining it as the rate at which work is done. He emphasizes the importance of understanding the relationship between power (measured in watts), work, and time. Through relatable examples involving moving a sofa, lifting weights, and a cyclist maintaining speed, Mr. Fullerton illustrates how power is calculated and how different scenarios can lead to varying power outputs. The video concludes with a comparison of power between two aliens lifting children, highlighting the significance of time in power calculation.
Takeaways
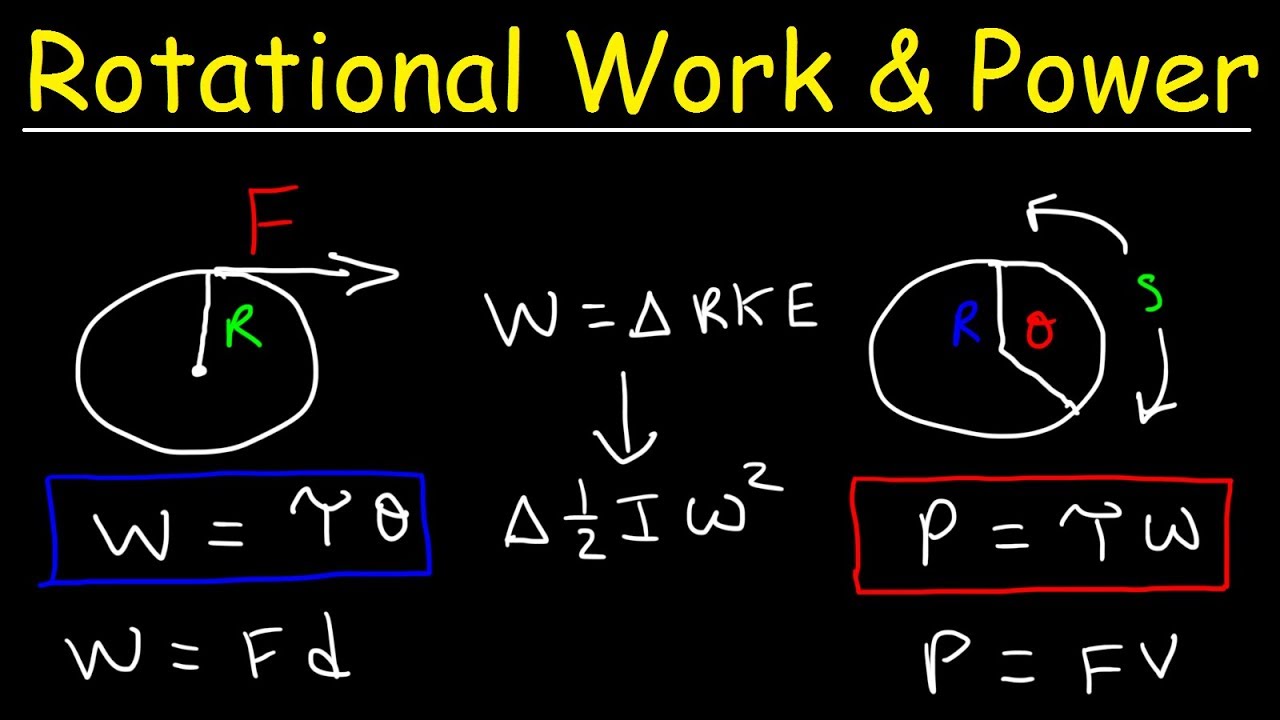
- 📚 Power is defined as the rate at which work is done, calculated as work done divided by the time taken to do that work.
- ⏱️ The unit of power is the watt (W), which is equivalent to a joule per second (J/s).
- 🔢 Capital 'P' represents power, and it's crucial to distinguish it from 'W' which represents work.
- 💡 When the same amount of work is done, the faster it is performed, the higher the power output.
- 🛋️ Example: Bob and Peter move a sofa with a 200 N force in 6 seconds, resulting in 100 W of power.
- 🏋️♂️ Kevin moves the same sofa with the same force but in 12 seconds, resulting in 50 W of power.
- 🔧 Power can also be calculated as force times average velocity (P = F * v_avg).
- 🏗️ Motor A lifts a 5000 N load at 2 m/s², producing 10 kW of power, while Motor B lifts a 4000 N load at 3 m/s², producing 12 kW of power.
- 🚴♂️ A 70 kg cyclist develops 210 W of power at a constant velocity of 7 m/s, exerting an average force of 30 N.
- 👽 Alien A lifts a 500 N child 0.4 m in 2 seconds with a power output of 100 W, while Alien B lifts a 400 N student 0.5 m in 1 second with a power output of 200 W.
- 📈 Power is directly proportional to the time taken to do work; less time for the same work results in higher power.
- 🔗 For more information and help, the script suggests visiting WWE plus physics.com.
Q & A
What is the definition of power?
-Power is the rate at which work is done, calculated as the work done divided by the time it took to do that amount of work.
What are the units of power?
-The units of power are joules per second, which is also known as a watt, abbreviated as W.
How can the same amount of work result in different power outputs?
-The same amount of work can result in different power outputs if it takes different amounts of time to complete, as power is directly related to the time taken to do the work.
In the example with Bob and Peter, what is the formula used to calculate the power they supplied?
-The formula used to calculate the power supplied by Bob and Peter is P = F * cos(theta) / T, where P is power, F is the force, theta is the angle between the force and displacement, and T is the time.
How much power did Bob and Peter supply when moving the sofa?
-Bob and Peter supplied 100 watts of power when moving the sofa, using the formula P = 200 N * 3 m / 6 s.
How does the formula for power differ when considering force and average velocity?
-When considering force and average velocity, the formula for power simplifies to P = F * v, where P is power, F is the force, and v is the average velocity.
Which motor, A or B, supplies more power when lifting weights at different velocities?
-Motor B supplies more power, with 12,000 watts (12 kilowatts), compared to Motor A's 10,000 watts (10 kilowatts).
How can you calculate the average force exerted by the cyclist in the given example?
-The average force exerted by the cyclist can be calculated using the formula F = P / v, where F is the force, P is the power (210 watts), and v is the average velocity (7 m/s), resulting in a force of 30 N.
What is the power developed by Alien A when lifting a 500-Newton child to a height of 0.4 meters in 2 seconds?
-The power developed by Alien A is 100 watts, calculated using the formula P = F * h / t, where F is the force (500 N), h is the height (0.4 m), and t is the time (2 s).
In the comparison between Alien A and Alien B, who developed more power when lifting weights?
-Alien B developed more power, with 200 watts, even though both aliens did the same amount of work (200 joules), as Alien B completed the work in a shorter time (1 second).
What is the main takeaway from the mini lesson on work and power?
-The main takeaway is understanding the relationship between work, power, and time, and how different scenarios can affect the power output, even when the same amount of work is done.
Outlines
📚 Introduction to Power and Calculation
This paragraph introduces the concept of power, explaining it as the rate at which work is done. It emphasizes the importance of understanding the relationship between power (P), work, and time. The unit of power is the watt (W), which is equivalent to joules per second. The paragraph uses examples of Bob and Peter moving a sofa and Kevin pushing the same sofa to illustrate how the time taken to do the same amount of work affects power output. It also introduces an alternative calculation for power, which is force times average velocity, and applies this to scenarios involving motors lifting weights at different velocities.
🚴♂️ Calculating Power in Real-World Scenarios
This paragraph delves into practical applications of power calculation through various scenarios. It starts with a cyclist maintaining a constant velocity and calculates the average force exerted on the bicycle. The paragraph then presents a problem involving aliens lifting children and compares the power developed by two different aliens. The focus is on understanding how the time taken to do work affects the power output, even when the same amount of work is done. The paragraph concludes by encouraging further exploration of physics concepts.
Mindmap
Keywords
💡Power
💡Work
💡Joule
💡Watt
💡Force
💡Displacement
💡Time
💡Average Velocity
💡Efficiency
💡Cosine Theta (cos θ)
💡Acceleration
Highlights
Power is defined as the rate at which work is done.
Power is calculated as work done divided by the time taken to do that work.
The unit of power is joules per second, also known as a watt, abbreviated as W.
The same amount of work can have different power outputs depending on the time taken.
Bob and Peter move a sofa with a combined force of 200 Newtons over 3 meters in 6 seconds, resulting in 100 watts of power.
Kevin moves the same sofa with a force of 200 Newtons over 3 meters in 12 seconds, resulting in 50 watts of power.
Power can also be calculated as force times average velocity.
Motor A lifts a 5000 Newton steel crossbar at 2 meters per second, supplying 10,000 watts or 10 kilowatts of power.
Motor B lifts a 4000 Newton steel support at 3 meters per second, supplying 12,000 watts or 12 kilowatts of power.
A 70 kg cyclist develops 210 watts of power at a constant velocity of 7 meters per second east.
Alien A lifts a 500 Newton child 0.4 meters in 2 seconds with a power output of 100 watts.
Alien B lifts a 400 Newton student 0.5 meters in 1 second with a power output of 200 watts.
Despite doing the same amount of work, Alien B develops more power due to the shorter time taken.
Understanding power and its calculation is crucial for solving various physics problems.
The lecture provides practical examples to illustrate the concept of power in real-world scenarios.
The relationship between work, force, displacement, and time is fundamental in power calculations.
The lecture emphasizes the importance of distinguishing between work (capital W) and power (capital P) with correct units.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: