prefixes in measurement explained and how to use them

PhysicsHigh
27 Jul 202005:58
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Paul from Physics High embarks on a journey through the evolution of computer storage, starting from a modest 64 kilobytes to an impressive 10-12 terabytes. He uses his personal computing history to introduce the concept of prefixes like kilo, mega, giga, and tera, which simplify the understanding of large numbers. Paul explains how these prefixes, used in various scientific measurements, represent powers of ten and are crucial for converting units into understandable terms. Through examples like the wavelength of light and the frequency of a radio station, viewers learn to apply these prefixes in practical situations, enhancing their comprehension of scientific notation and unit conversions.

Takeaways
  • πŸ“ˆ The speaker, Paul, illustrates the exponential growth in computer storage capacity over the years, highlighting the importance of understanding numerical prefixes for comprehending large data sizes.
  • πŸ”’ Prefixes are used to simplify the expression of large or small numbers by attaching them to base units, making it easier to conceptualize and work with the numbers in scientific contexts.
  • πŸ” The script emphasizes the importance of converting these prefixes into their corresponding powers of ten when performing calculations, to ensure accuracy in scientific and mathematical problems.
  • 🌐 Paul's journey from a 64 kilobyte computer in 1984 to a system with 10-12 terabytes of storage today exemplifies the rapid advancements in technology and data storage capabilities.
  • πŸ“ Basic units of measurement like meters and grams can be converted into more manageable figures using prefixes such as millimeters and kilograms, which are one thousandth and one thousand of the base units, respectively.
  • πŸ’‘ The script explains that the most common prefixes used in the sciences are related to powers of three (e.g., kilo, mega, giga, tera) and their corresponding negative exponents (e.g., milli, micro, nano).
  • πŸ“‹ When dealing with measurements, such as the wavelength of light or the frequency of a radio wave, it's crucial to convert the prefixed units into their SI unit equivalents for accurate calculations.
  • 🌟 The example of converting 632 nanometers to meters as 6.32 Γ— 10^(-7) meters in scientific notation demonstrates the practical application of understanding and using numerical prefixes correctly.
  • πŸ“ The relationship between the speed of light and the frequency of a radio wave is used to calculate the associated wavelength, showcasing the interplay between different scientific concepts and units.
  • πŸŽ“ Paul's explanation serves as an educational tool for understanding the significance of prefixes in science and mathematics, encouraging viewers to stay informed and engaged with these concepts.
  • πŸ‘‹ The video concludes with a friendly reminder of the importance of these prefixes and an invitation for viewers to continue learning and exploring the sciences.
Q & A

  • What was the storage capacity of Paul's first computer?

    -Paul's first computer had a storage capacity of 64 kilobytes.

  • How did Paul's computer storage capacity evolve over the years?

    -Paul's computer storage capacity evolved from 64 kilobytes to 40 megabytes, then to 2 gigabytes, and finally to between 10 and 12 terabytes.

  • What is the purpose of using prefixes in measurements according to the script?

    -Prefixes are used in measurements to help make sense of large or small numbers by representing different sizes, making them easier to conceptualize and work with in mathematical problems and sciences.

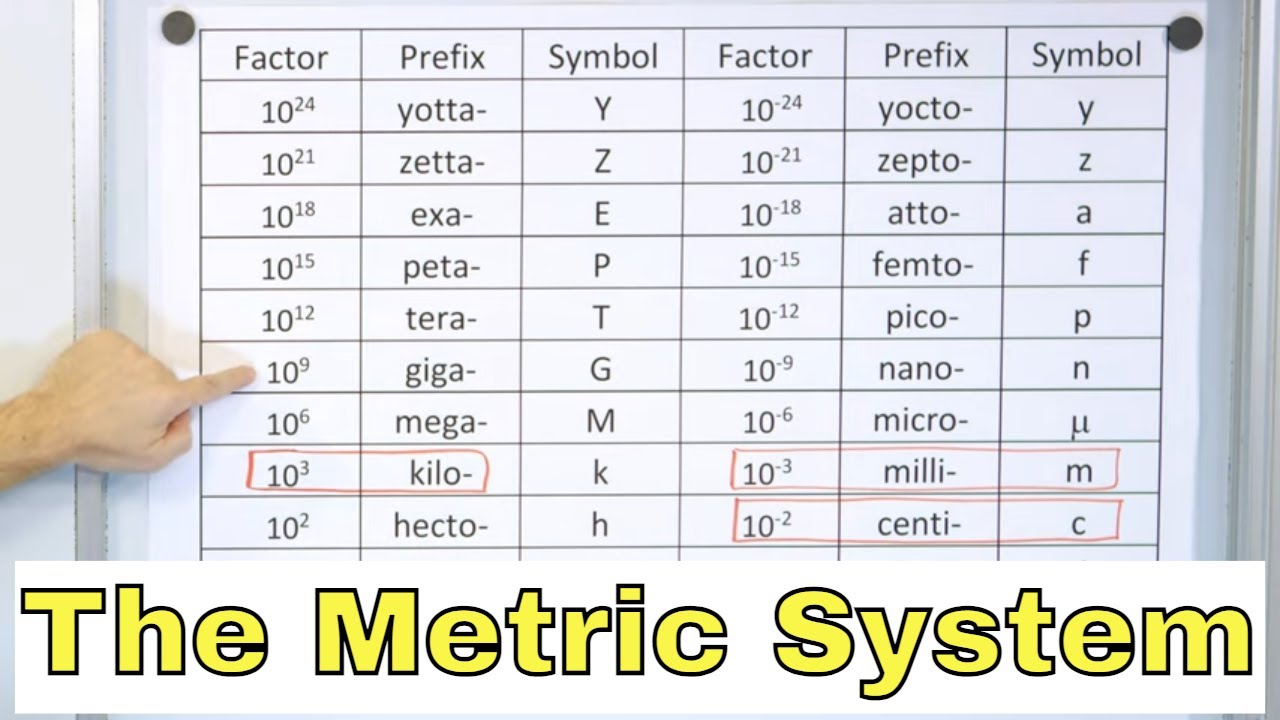
  • What is the prefix for 10 to the power of 3?

    -The prefix for 10 to the power of 3 is 'kilo', symbolized as 'k'.

  • What is the prefix for 10 to the power of 6?

    -The prefix for 10 to the power of 6 is 'mega', symbolized as 'M'.

  • What is the prefix for 10 to the power of 9?

    -The prefix for 10 to the power of 9 is 'giga', symbolized as 'G'.

  • What is the prefix for 10 to the power of 12?

    -The prefix for 10 to the power of 12 is 'tera', symbolized as 'T'.

  • How does one convert a prefix to its corresponding power for calculations?

    -To convert a prefix to its corresponding power for calculations, one must replace the prefix with the negative exponent value it represents. For example, 'nano' which stands for 10 to the power of negative 9, should be replaced with '-9' when doing calculations.

  • What is the SI unit for 'milli'?

    -The SI unit for 'milli' is 10 to the power of negative 3, representing one-thousandth of a unit.

  • What is the SI unit for 'micro'?

    -The SI unit for 'micro' is 10 to the power of negative 6, representing one-millionth of a unit.

  • How can one remember the meaning of 'nano' quickly?

    -One can remember the meaning of 'nano' by associating the letter 'n' in the prefix with the negative 9 it represents, as 'nano' equals 10 to the power of negative 9.

  • What is the formula to calculate the wavelength of a radio wave?

    -The formula to calculate the wavelength of a radio wave is the speed of light divided by the frequency of the wave. The speed of light is 3 times 10 to the power of 8 meters per second.

  • What is an example of using prefixes to simplify the expression of numbers?

    -An example of using prefixes to simplify the expression of numbers is expressing 10 kilometers as '10 km' instead of '10,000 meters', which makes the number easier to conceptualize and work with.

Outlines
00:00
πŸ“ˆ Evolution of Personal Computing Storage

This paragraph narrates the personal journey of Paul from Physics Hired with the evolution of his computer storage capacities. Starting with a 64 kilobyte hard drive in 1984, Paul describes the exponential growth in storage capacity over the years, highlighting the transition from kilobytes to terabytes. He emphasizes the importance of understanding prefixes in grasping these large numbers, which are crucial when dealing with measurements in the sciences. Paul explains how prefixes like kilo, mega, giga, and tera represent powers of three and how they can be used to make sense of vast quantities, such as storage sizes. He also introduces the concept of converting these prefixes back to their corresponding powers of ten when performing calculations, using the example of converting nanometers to meters in scientific notation.

05:02
πŸ“‘ Understanding Prefixes in Scientific Measurements

In this paragraph, Paul continues the discussion on scientific prefixes and their application in measurements, particularly in the context of wavelength calculations. He uses the example of a radio station frequency to illustrate how to calculate the associated wavelength by dividing the speed of light by the frequency. Paul emphasizes the need to convert the frequency measurement from megahertz to its correct unit (hertz) before performing the calculation, resulting in the appropriate length for the radio wave. This segment of the video script underscores the practical application of understanding and manipulating scientific prefixes for accurate problem-solving in various scientific fields.

Mindmap
Keywords
πŸ’‘Computer Storage
The term 'Computer Storage' refers to the amount of data that can be stored on a computer system. In the video, Paul uses the evolution of his personal computer's storage capacity as an example to illustrate the vast growth in technology over the years, from 64 kilobytes to 10 to 12 terabytes. This progression helps viewers grasp the concept of large numbers and the importance of prefixes in expressing them more understandably.
πŸ’‘Prefixes
In the context of the video, 'Prefixes' are used to denote different orders of magnitude in measurements, particularly in the field of computer storage and science in general. Prefixes help simplify the expression of large or small numbers by attaching a specific symbol and value to them, such as kilo (10^3), mega (10^6), giga (10^9), and tera (10^12). The video emphasizes the importance of understanding these prefixes for better conceptualization and calculation in scientific problems.
πŸ’‘Measurement Units
Measurement units are standardized quantities used to express the magnitude of physical properties such as length, mass, and time. In the video, Paul discusses how prefixes are commonly used with measurement units to create more understandable expressions of large or small values. For example, a millimeter is one thousandth of a meter, and a kilogram is a thousand grams.
πŸ’‘Scientific Notation
Scientific notation is a way of expressing numbers as a product of a number between 1 and 10 and a power of 10, which simplifies the writing and calculation of very large or small numbers. In the video, Paul explains that when dealing with computer storage or wavelengths, it's often necessary to convert the values with prefixes back into their scientific notation for calculations.
πŸ’‘Engineering Notation
Engineering notation is a subset of scientific notation where the number is expressed in a power of 10 that is a multiple or fraction close to a round number, typically within one order of magnitude. It is often used in engineering and sciences to simplify calculations and make numbers more readable. In the video, Paul refers to engineering notation when he replaces the prefix 'nano' with its corresponding power of 10, -9, in his calculation.
πŸ’‘Frequency
Frequency refers to the rate at which a repeating event occurs over a given period of time. In the context of the video, Paul uses the frequency of a radio station as an example to explain how understanding prefixes and units is crucial in calculating related physical properties, such as wavelength.
πŸ’‘Wavelength
Wavelength is the spatial distance between successive identical points in a wave, such as the peaks or troughs. In the video, Paul discusses the relationship between frequency and wavelength, using the example of a radio wave to demonstrate how understanding prefixes and unit conversions is essential for accurate scientific calculations.
πŸ’‘Speed of Light
The speed of light is the constant speed at which light, or other electromagnetic radiation, travels in a vacuum. It is approximately 3 x 10^8 meters per second and is a fundamental constant in physics. In the video, Paul uses the speed of light as a basis for calculating the wavelength of a radio wave, emphasizing the importance of using correct units and values in scientific calculations.
πŸ’‘Conversion
Conversion in the context of the video refers to the process of changing a physical quantity from one unit to another. This is essential in scientific calculations where values expressed in different units need to be converted to a common unit before performing operations. Paul explains how to convert values with prefixes, such as replacing 'nano' with its corresponding power of 10, to perform calculations accurately.
πŸ’‘Power of Three
The term 'Power of Three' relates to the concept of multiplying a number by itself three times, which is commonly used in the metric system for defining large prefixes. In the video, Paul mentions that many of the basic prefixes used in science are to the power of three or multiples thereof, such as kilo (10^3), mega (10^6), and tera (10^12).
πŸ’‘Conceptualization
Conceptualization in this context refers to the mental process of forming an idea or understanding of something abstract or complex. Paul emphasizes in the video the importance of using prefixes to help conceptualize large or small numbers, making them easier to grasp and work with in scientific calculations.
Highlights

Paul shares his personal story of computer storage evolution, from 64 kilobytes to 10 to 12 terabytes.

The importance of understanding prefixes in the context of science and measurements is emphasized.

The use of prefixes allows for more comprehensible representation of large or small numbers.

The basic unit of measurement is established as 1, without a prefix.

Kilo, representing 10 to the power of 3, is introduced with its symbol 'k'.

Mega, giga, and tera are identified as common prefixes with their respective symbols 'M', 'G', and 'T'.

Milli, micro, and nano are explained as prefixes for smaller units, with their symbols 'm', 'ΞΌ', and 'n'.

Deca, deci, centi, and centa are mentioned as prefixes outside the power of three pattern.

The process of converting prefixes back to their SI unit values for calculations is described.

An example of converting nanometers to meters for calculation purposes is provided.

Engineering notation is introduced as a method for calculations involving large or small numbers.

Scientific notation is also mentioned as a way to express very large or small numbers.

A practical application of using radio frequency and wavelength with appropriate unit conversion is demonstrated.

The importance of using correct units in calculations for accurate results is highlighted.

Paul's aim to educate about the nature and use of prefixes in science is shared.

The transcript concludes with Paul's sign-off, reinforcing the educational value of the content.

Transcripts

Browse More Related Video

Learn Metric Units & Unit Conversions (Meters, Liters, Grams, & more) - [5-8-1]

Converting units of measurement with scientific notation (3 examples)

02 - Learn Unit Conversions, Metric System & Scientific Notation in Chemistry & Physics

The Metric System and SI Units in Physics - [1-1-3]

Chemistry Reference table C

metric unit conversions shortcut: fast, easy how-to with examples

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ComputerHistoryStorageGrowthMetricPrefixesScienceEducationMathematicsUnitConversionEngineeringNotationPhysicsEducationalContentInformativeVideo