Conceptual understanding of flux in three dimensions | Multivariable Calculus | Khan Academy

Khan Academy

30 May 201208:22

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the concept of a three-dimensional function, 'rho', representing mass density of a fluid, and another vector function, 'v', representing the fluid's velocity. It introduces a third function 'f', the product of 'rho' and 'v', interpreted as momentum density. The script then explores the calculation of a surface integral of 'f' over a given surface, emphasizing its analogy to two-dimensional line integrals. The surface integral is conceptualized as the measure of mass passing through a surface per unit time, with applications ranging from water vapor in a bathroom to the flow of a river through a net.

Takeaways

📌 The concept introduces a 3D function 'rho' representing mass density of a fluid at any point in three dimensions.
📌 A scalar function is mentioned that provides a numerical value at every point in 3D space.
📌 The vector function 'v' describes the velocity of the fluid or gas at any point in three dimensions.
📌 A new function 'f' is defined as the product of 'rho' and 'v', which can be visualized as momentum density.
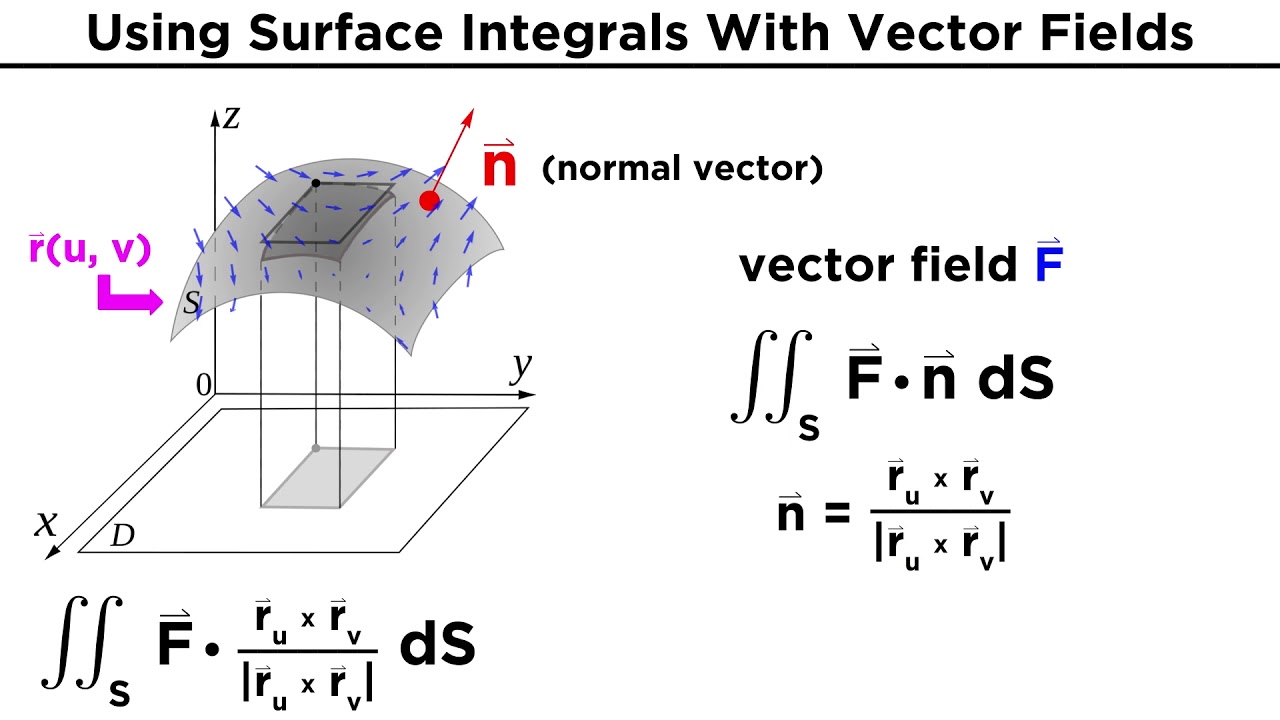
📌 The surface integral of function 'f' is considered, which involves the dot product of 'f' and the unit normal vector 'n' at each point on the surface 'dS'.
📌 The dot product essentially measures the component of 'f' that is normal to the surface, indicating the magnitude of this component.
📌 The units of 'f' are derived from the units of mass density and velocity, resulting in units of kilogram per second, representing the mass flow rate.
📌 The concept is analogous to the flux through a two-dimensional surface, applicable to scenarios like water vapor escaping through a bathroom window.
📌 The function 'f' can be used to calculate the mass of fluid flowing through a surface, such as water through a net in a river.
📌 The video script aims to provide a conceptual understanding of how to evaluate and interpret surface integrals in three-dimensional spaces.

Q & A

What is the function rho in the context of the script?
-The function rho represents the mass density of a fluid, which can be a gas or liquid like water, at any point in three-dimensional space.
What is the significance of the scalar function mentioned in the script?
-The scalar function mentioned provides a numerical value at any point in 3D space, although the specific nature of this function is not detailed in the script.
What does the vector function v represent?
-The vector function v represents the velocity of the fluid or gas at any point in three dimensions, providing both magnitude and direction.
How is the function f defined in relation to rho and v?
-The function f is defined as the product of rho and v, essentially giving a vector that represents the momentum density at any point in three-dimensional space.
What is the physical interpretation of the dot product f dot n?
-The dot product f dot n calculates the component of f that is normal to the surface, which can be interpreted as the magnitude of the momentum density perpendicular to the surface.
What does the surface integral of f dot n evaluate?
-The surface integral of f dot n evaluates the total mass, in kilograms per second, that is crossing a given surface at any moment in time.
How can the concept of f be visualized in a real-world scenario?
-The concept of f can be visualized as the mass of water vapor traveling through an open window in a bathroom, or the mass of river water flowing through a net placed within it.
What units does the function f have?
-The units of f are derived from the units of mass density (rho) and velocity (v), resulting in kilograms per second.
What is the role of the unit normal vector n in the calculation of the surface integral?
-The unit normal vector n specifies the direction that is perpendicular to the surface, allowing the dot product to determine the component of f that is normal to the surface.
How does the script relate the concept of a surface integral to line integrals?
-The script explains that the surface integral of f dot n is analogous to the flux through a two-dimensional surface, similar to how line integrals deal with one-dimensional paths.
What will be covered in the subsequent videos after the script?
-The subsequent videos will discuss how to calculate the surface integral and represent it in different ways, providing practical methods for applying the concepts introduced in the script.

Outlines

00:00

📐 Introduction to 3D Fluid Dynamics

This paragraph introduces the concept of operating in three dimensions with a function, rho (ρ), representing the mass density of a fluid at any point in space. It also presents two additional functions: a scalar function that assigns a numerical value to each point in 3D space and a vector function, v, representing the velocity of the fluid. The paragraph further discusses the product of rho and v, conceptualizing it as a vector that maintains the direction of velocity but modifies its magnitude, potentially representing momentum density. The goal is to evaluate the surface integral of this function f over a given surface, which involves understanding the units and the physical interpretation of the integral as it relates to the mass flow through a surface area.

05:02

🔢 Understanding the Surface Integral and its Physical Interpretation

This paragraph delves into the units and conceptual understanding of the surface integral of the function f, which is the product of mass density (rho) and velocity (v). It explains how the units of f are derived from the units of rho and v, resulting in kilograms per second, which can be interpreted as the rate of mass flow through a surface. The paragraph uses the analogy of water vapor in a bathroom and the flux through a 2D surface to illustrate this concept. It also introduces the idea of evaluating the integral over a net-like surface to determine the mass of fluid flowing through it at any given moment, providing a practical application of the surface integral in understanding fluid dynamics.

Mindmap

Keywords

💡three dimensions

The term 'three dimensions' refers to a geometric space that is characterized by three axes—typically labeled as x, y, and z—which are used to determine the position of a point in space. In the context of the video, it is the setting within which the fluid's mass density and velocity are defined, allowing for a comprehensive analysis of the fluid's behavior in a 3D space.

💡mass density

Mass density is a measure of the amount of mass per unit volume of a substance. In the video, it is represented by the function rho (ρ), which varies with position in the three-dimensional space and is crucial for understanding how the fluid's mass is distributed throughout the volume.

💡scalar function

A scalar function is a mathematical function that associates each point in a given space with a single numerical value, as opposed to a vector function which associates points with vectors. In the video, the scalar function is used to describe a property that varies from point to point in 3D space but does not involve direction.

💡vector function

A vector function maps each point in a space to a vector, which has both magnitude and direction. In the context of the video, the vector function v represents the velocity of the fluid at every point in three dimensions, providing information on how the fluid moves through space.

💡momentum density

Momentum density is a concept that relates the mass density of a substance with its velocity, effectively describing the amount of momentum per unit volume. In the video, the function f, which is the product of rho and v, is analogous to momentum density, capturing how much momentum is carried by the fluid at any point in space.

💡surface integral

A surface integral is a mathematical operation that extends the concept of an integral over a line (line integral) to a two-dimensional surface. It involves calculating the cumulative effect of a function over the points on a surface, represented by the integral of the function dot product with the surface's unit normal vector.

💡unit normal vector

A unit normal vector is a vector of magnitude 1 that is perpendicular to a surface at a given point. It is used in surface integrals to determine the direction and orientation of the surface with respect to the function being integrated. In the video, the unit normal vector n is used to calculate the surface integral of the function f.

💡dot product

The dot product is a binary operation that takes two vectors and returns a scalar value. It is calculated as the product of the magnitudes of the two vectors and the cosine of the angle between them. In the context of the video, the dot product is used to find the component of the function f that is in the direction of the unit normal vector n.

💡flux

In physics, flux refers to the rate at which a quantity such as mass, energy, or particles crosses a given surface. The concept is used to describe the flow of a substance through a boundary. In the video, the term is used to describe the mass of the fluid that is passing through a surface, such as a window or a net, per unit of time.

💡velocity

Velocity is a vector quantity that describes the speed of an object in a specific direction. In the context of the video, the function v represents the velocity of the fluid at every point in three-dimensional space, which is essential for understanding how the fluid moves and how its mass density is carried along with it.

💡units of measurement

Units of measurement are standardized quantities that are used to express the magnitude of physical quantities. In the video, units are crucial for understanding the physical meaning of the mathematical expressions and ensuring that the calculations are dimensionally consistent.

Highlights

Exploring a three-dimensional function, rho, representing the mass density of a fluid at any point in space.

Introducing a scalar function that provides a numerical value at any point in 3D space.

Defining a vector function, v, that gives the velocity of the fluid or gas at every point in three dimensions.

Creating a new function, f, which is the product of rho and v, representing a vector that could be conceptualized as momentum density.

Discussing the extension of concepts from two-dimensional line integrals to three-dimensional surface integrals.

Evaluating the surface integral of function f over a given surface, represented as f dot n where n is the unit normal vector.

Explaining that the dot product of two vectors indicates the magnitude of the component of f in the direction of the normal vector.

Describing the units of f as a combination of mass density and velocity units, resulting in units of kilogram per second.

Interpreting the surface integral of f as a measure of the mass of substance crossing a surface per unit of time.

Drawing an analogy between the flux through a two-dimensional surface and the mass of water vapor passing through an open window.

Using the example of a river to illustrate how the function f can represent the momentum density at any point and how a net could be used to measure the mass flow.

Emphasizing the practical application of these concepts in understanding the flow of fluids, such as water vapor or river water, through a given surface.

Outlining the plan to discuss in future videos how to calculate and represent these integrals in various ways.

Providing a conceptual understanding of the mathematical concepts through relatable examples like bathroom water vapor and river flow.

Highlighting the importance of the normal vector in determining the direction of the flow of mass across a surface.

Clarifying the role of the surface integral in determining the total mass flow across a surface at any given moment.

Transcripts

Browse More Related Video

Evaluating Surface Integrals

Conceptual clarification for 2D divergence theorem | Multivariable Calculus | Khan Academy

Surface integral ex2 part 1: Parameterizing the surface | Multivariable Calculus | Khan Academy

Constructing a unit normal vector to a surface | Multivariable Calculus | Khan Academy

Vector representation of a surface integral | Multivariable Calculus | Khan Academy

Evaluating Line Integrals

Conceptual understanding of flux in three dimensions | Multivariable Calculus | Khan Academy

Takeaways

Q & A

What is the function rho in the context of the script?

What is the significance of the scalar function mentioned in the script?

What does the vector function v represent?

How is the function f defined in relation to rho and v?

What is the physical interpretation of the dot product f dot n?

What does the surface integral of f dot n evaluate?

How can the concept of f be visualized in a real-world scenario?

What units does the function f have?

What is the role of the unit normal vector n in the calculation of the surface integral?

How does the script relate the concept of a surface integral to line integrals?

What will be covered in the subsequent videos after the script?