How to lie using visual proofs
TLDRThe video script discusses three intriguing fake mathematical proofs, each with increasing subtlety. The first incorrectly calculates the surface area of a sphere by unfolding it into a rectangle, while the second mistakenly proves that pi equals 4 by approximating a circle with jagged curves. The third, a Euclidean-style argument, falsely claims all triangles are isosceles due to a subtle error in constructing the angle bisector. These examples highlight the importance of rigorous thinking and critical analysis in mathematics, despite the elegance and intuitive appeal of visual proofs.
Takeaways
- 🔍 The script discusses three fake proofs and their implications for understanding mathematical concepts and the importance of rigor in proofs.
- 🔵 The first fake proof attempts to calculate the surface area of a sphere by unfolding its slices into a rectangle, but fails because the edges don't align perfectly, leading to an incorrect result.
- 🌐 The second proof is a classic argument that pi equals 4, based on approximating a circle with a square and then refining the shape, which is incorrect due to a misinterpretation of limits.
- 📐 The third proof, presented as a Euclidean-style argument, claims all triangles are isosceles, but contains a subtle error in the construction of the angle bisector.
- 🌀 The key issue with the sphere proof is the non-linear relationship between the width of the slices and their position on the sphere, leading to an overlap that doesn't disappear even with finer subdivisions.
- 🔍 The circle approximation example highlights the importance of understanding the limits of shapes and the need for rigorous mathematical proofs rather than relying solely on visual intuition.
- 📊 The script emphasizes that visual proofs, while helpful, cannot replace critical thinking and the need to identify hidden assumptions and edge cases.
- 🤔 The false proofs serve as educational tools to illustrate common pitfalls in mathematical reasoning and the necessity of a rigorous approach to proofs.
- 🔑 The concept of 'Gaussian curvature' is mentioned as a relevant term when discussing the geometry of curved surfaces versus flat space, indicating the complexity of dealing with spherical geometry.
- 🔎 The script concludes by reinforcing the message that while visual intuition is valuable, it must be complemented with critical thinking to avoid falling into the traps presented by seemingly convincing but incorrect mathematical arguments.
Q & A
What is the main topic of the transcript?
-The main topic of the transcript is the discussion of three fake proofs and their implications for understanding mathematical concepts and the importance of rigor in mathematical proofs.
What is the first fake proof about?
-The first fake proof is about a formula for the surface area of a sphere, which incorrectly suggests that the surface area can be calculated as pi squared times the radius squared, instead of the correct formula, which is 4 pi times the radius squared.
What is the issue with the fake proof for the surface area of a sphere?
-The issue with the fake proof is that it assumes that the unfolded surface of the sphere can be approximated as a perfect rectangle, which is not the case due to the non-linear relationship between the width of the wedges and their position on the sphere.
What is the second fake proof discussed in the transcript?
-The second fake proof is a simple argument that claims pi is equal to 4, based on a sequence of jagged curves that approximate a circle, with the incorrect assumption that the limit of these curves has a perimeter of 8, leading to the false conclusion about the value of pi.
Why is the second proof incorrect?
-The second proof is incorrect because it confuses the limit of the lengths of the curves with the length of the limit of the curves. The limit of the lengths is indeed 8, but this does not mean that the length of the limit of the curves, which is the actual circle, is also 8.
What is the third fake proof presented in the transcript?
-The third fake proof is a Euclid-style argument that falsely claims that all triangles are isosceles, based on incorrect assumptions and constructions, particularly with the angle bisector and the perpendicular lines drawn within the triangle.
What is the subtle mistake in the third fake proof?
-The subtle mistake in the third fake proof is the incorrect assumption that the intersection point of the angle bisector and the perpendicular bisector lies inside the triangle, which leads to false congruence claims and the incorrect conclusion that all triangles are isosceles.
What is the key lesson from the discussion of these fake proofs?
-The key lesson is that while visual intuition and diagrams can help elucidate mathematical concepts, they cannot replace rigorous critical thinking and the need to carefully examine hidden assumptions and edge cases in mathematical proofs.
How does the transcript relate to the broader theme of mathematical rigor?
-The transcript emphasizes the importance of mathematical rigor by showing how visually appealing but flawed proofs can lead to incorrect conclusions. It highlights the necessity of step-by-step deductive reasoning from axioms to establish mathematical truths accurately.
What is the significance of the example with the sphere and the concept of Gaussian curvature?
-The example with the sphere illustrates that the geometry of a curved surface, such as a sphere, is fundamentally different from the geometry of flat space, and that one cannot accurately flatten a sphere without accounting for its Gaussian curvature, which affects the local geometry and the area of the surface.
What is the relevance of the discussion on limiting arguments in the context of calculus?
-The discussion on limiting arguments is relevant to calculus because it highlights the need for care when using approximations, such as approximating the area under a curve with rectangles. It underscores the importance of understanding the error in these approximations and ensuring that the error approaches zero in the limit for the results to be valid.
Outlines
📐 Exploring False Proofs in Mathematics
This paragraph introduces the topic of discussing three fake proofs in mathematics, starting with a flawed proof for the surface area of a sphere. The proof involves subdividing the sphere into slices and unraveling them to form a shape whose area is mistakenly assumed to be that of a perfect rectangle, leading to an incorrect formula for the sphere's surface area. The paragraph also touches on the importance of critical thinking in mathematics and the limitations of relying solely on visual intuition.
🔍 The Pitfalls of Visual Intuition
The second paragraph delves into the reasons why the initial example of the sphere's surface area is incorrect, emphasizing the need for rigor in mathematical proofs. It then presents a seemingly plausible argument that pi equals 4 by approximating a circle with a square and its tangents. The paragraph highlights the nuances of this example and the importance of understanding the limit of a sequence of curves, which is a critical aspect of calculus. However, it points out that despite the visual appeal, the argument is flawed because it assumes that the limit of the lengths of the approximating curves is the length of the limit curve itself.
🤔 Deconstructing a False Euclidean Proof
This paragraph presents a false Euclidean-style proof that all triangles are isosceles, which is clearly incorrect. The paragraph challenges the audience to identify the subtle error in the proof. The proof involves constructing perpendicular bisectors and angle bisectors, leading to a series of congruent triangles and ultimately to the false conclusion that all triangles are isosceles. The paragraph ends by posing three possibilities: that all triangles are indeed equilateral, that Euclidean reasoning can lead to false results, or that there is an error in the proof, leaving the audience to ponder the true nature of the mistake.
🧩 Understanding the Geometry Behind False Proofs
The fourth paragraph provides an in-depth analysis of the geometry behind the false proofs discussed earlier. It explains why the sphere example fails due to the non-linear relationship between the width of the sphere's wedges and the angle from the z-axis. The paragraph also contrasts this with the valid proof involving pizza slices, highlighting the difference in how the shapes are flattened and the importance of Gaussian curvature in understanding the geometry of curved surfaces. The paragraph concludes with a discussion on the subtleties of limiting arguments and the critical need for precision and awareness of hidden assumptions in mathematical reasoning.
Mindmap
Keywords
💡Surface Area
💡Sphere
💡False Proof
💡Visual Intuition
💡Limit
💡Circle
💡Pi (π)
💡Euclidean Proof
💡Congruence
💡Gaussian Curvature
💡Critical Thinking
Highlights
The talk introduces three fake proofs, each with increasing subtlety, to discuss their implications for understanding math.
The first fake proof is about the surface area of a sphere and involves subdividing the sphere into vertical slices.
The flawed logic in the sphere proof is that it assumes the limit of finer and finer slices results in a perfect rectangle, which is incorrect.
The true surface area of a sphere is 4 pi r squared, not pi squared times r squared as the first fake proof suggests.
The second fake proof is a simple argument that claims pi equals 4 by using a square inscribed in a circle with radius 1.
The circle approximation argument is flawed because it assumes that the limit of the perimeters of approximating shapes equals the circumference of the circle.
The third fake proof offers a Euclidean style argument that all triangles are isosceles, which is obviously false.
The isosceles triangle proof fails because it incorrectly assumes the intersection point of the perpendicular bisector and angle bisector lies inside the triangle.
The importance of rigor and critical thinking in math is emphasized, as visual intuition and proofs can be misleading without proper scrutiny.
The talk highlights the difference between true mathematical proofs and visually intuitive arguments that may not hold up under closer examination.
The sphere example illustrates the issue of applying limiting arguments without considering the local flatness of curved surfaces.
Gaussian curvature is mentioned as a relevant concept when discussing the geometry of curved surfaces versus flat space.
The circle approximation proof is contrasted with a valid proof involving pizza slices, highlighting the necessity of proper geometric transformations.
The talk concludes with the message that visual proofs, while helpful, cannot replace the need for critical analysis and awareness of hidden assumptions.
A rearrangement puzzle is used as an analogy to explain how area can seem to appear or disappear due to subtle geometric changes.
The importance of being wary of lines that appear straight without explicit confirmation is stressed in the context of the sphere proof.
The concept of limits and their proper application in calculus is discussed, particularly in approximating areas under curves.
Transcripts
Browse More Related Video

Lecture 08: Circles, Pyramids, Cones and Spheres
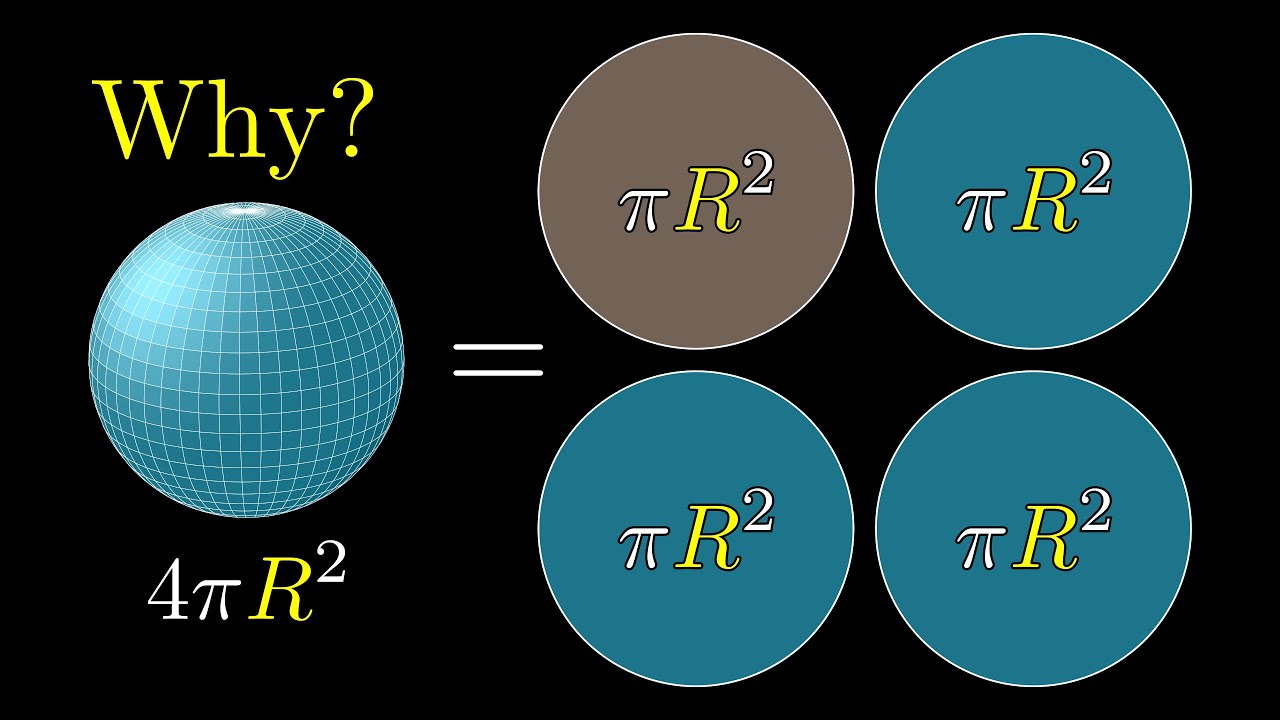
But why is a sphere's surface area four times its shadow?

Riemann approximation introduction | Accumulation and Riemann sums | AP Calculus AB | Khan Academy

Solid of Revolution (part 3)

The essence of calculus

How to do epsilon-delta proofs (ultimate calculus guide)
5.0 / 5 (0 votes)
Thanks for rating: