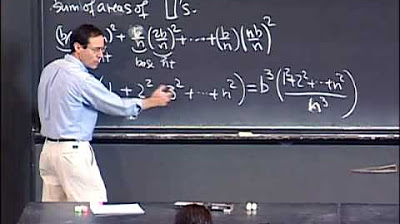Big Picture: Integrals
TLDRThis transcript from a calculus lecture introduces the concept of integrals, the inverse operation to differentiation. The professor explains how to move from knowing the slope (function two) to finding the height (function one) using the fundamental ideas of limits and summation. The process is illustrated with examples, emphasizing the accumulation of areas under the slope curve to approximate the original function. The lecture also touches on historical figures like Archimedes and the development of calculus by Newton and Leibniz.
Takeaways
- 📚 Calculus involves understanding the relationship between two functions: the height (y of x) and the slope (s of x).
- 🔄 The process of calculus often involves moving from knowing the slope (function two) to finding the height (function one), and vice versa.
- 📈 When dealing with straight lines, the slope is simply the rise (up) divided by the run (across).
- 🔢 For curved functions, the concept of the derivative (function two) is introduced by considering small distances and letting them approach zero.
- 👆 The reverse process of calculus involves integrating the slope function to find the height function, which can be done by recognizing patterns or using known formulas.
- 🌟 A key example is when the height function is x to the power of n, where the derivative is n times x to the power of n-1.
- 🔄 Understanding the reverse process often involves recognizing and applying the power rule, which states that the power drops by one when taking the derivative.
- 📊 The concept of integration is introduced as the reverse operation to differentiation, symbolized by the integral sign and the function s(x)dx.
- 🤔 The process of integration can be visualized as summing up the areas under the curve of the slope function as the steps (delta x) become infinitesimally small.
- 📈 The integral of a function can be thought of as the area under the curve of its derivative, which provides a way to move from the slope back to the height function.
- 💡 The video emphasizes the importance of understanding the fundamental processes of calculus, including the limit process and the relationship between functions and their derivatives and integrals.
Q & A
What are the two main functions discussed in the calculus lecture?
-The two main functions discussed are the height function, denoted as y of x, and the slope function, denoted as s of x.
How does the process of finding the slope of a function change when the function is curving?
-When the function is curving, the process involves taking a small distance across, a small distance up, dividing the two, and then letting the small distance get smaller and smaller, resulting in the derivative, which is the slope function.
What is the reverse process in calculus known as, and what does it involve?
-The reverse process is known as integration. It involves knowing the slope of a function at every point and using that information to find the height function, y of x, of the graph.
What is the significance of x to the nth power in the context of this lecture?
-x to the nth power is significant because it is a basic function that is commonly encountered in calculus. When y is x to the nth, the derivative (slope function) is n times x to the (n-1)th power.
How does the concept of limits come into play when going from the slope function back to the height function?
-The concept of limits is crucial because it involves taking the ratio of the change in y (delta y) to the change in x (delta x) and letting delta x approach 0, which gives the derivative at that point and allows us to find the original height function through integration.
What is the integral symbol used to represent in the context of calculus?
-The integral symbol represents the process of integration. It is used to denote the integral of a function with respect to x, which is the reverse process of differentiation.
How does the process of summing delta y's over individual steps relate to finding the original height function?
-Summing delta y's over individual steps is a way to approximate the original height function. By adding up all the changes in y (delta y's), we can recover the total change in y, which gives us the final height of the function.
What happens when the slope function is x to the nth power, and we want to find the corresponding height function?
-If the slope function is x to the nth power, the corresponding height function is x to the (n+1)th power divided by (n+1), so that when we differentiate it, the extra power cancels out, and we get back to x to the nth power as the slope.
How does the process of integration relate to the concept of area under a curve?
-Integration is fundamentally about finding the area under a curve. When we integrate a function, we are essentially summing up the infinitesimally small areas under the curve defined by the function's rate of change at each point.
What is the practical application of understanding the reverse process from slope to height in calculus?
-Understanding the reverse process from slope to height allows us to reconstruct the original function from its derivative, which is useful in various applications such as determining the total distance traveled given a rate of speed at different times, or finding the area under a curve representing various physical quantities.
What is the role of the function s of x in the context of this calculus lecture?
-The function s of x represents the slope of the tangent line to the graph of the height function y of x at any given point x. It is the derivative of the height function and provides the rate of change or slope at every point on the curve.
Outlines
📚 Introduction to Calculus Concepts
This paragraph introduces the fundamental concepts of calculus, focusing on the relationship between two functions: the height (y of x) and the slope (s of x). It explains how calculus is used to transition from one function to another, particularly from the height function to the slope function and vice versa. The discussion includes examples of power functions and the process of taking derivatives and integrals, highlighting the importance of recognizing patterns and applying algebraic manipulations to understand these mathematical processes.
🔄 Understanding the Reverse Process in Calculus
The second paragraph delves into the reverse process of calculus, which involves going from the slope function (s of x) back to the height function (y of x). It emphasizes the importance of recognizing the actual process behind this transformation, which involves limits and the concept of continuous change. The paragraph introduces the integral symbol and explains its connection to the sum of differential changes in the function, providing examples to illustrate how to recover the original function from its slope.
📈 Algebraic and Graphical Approach to Calculus
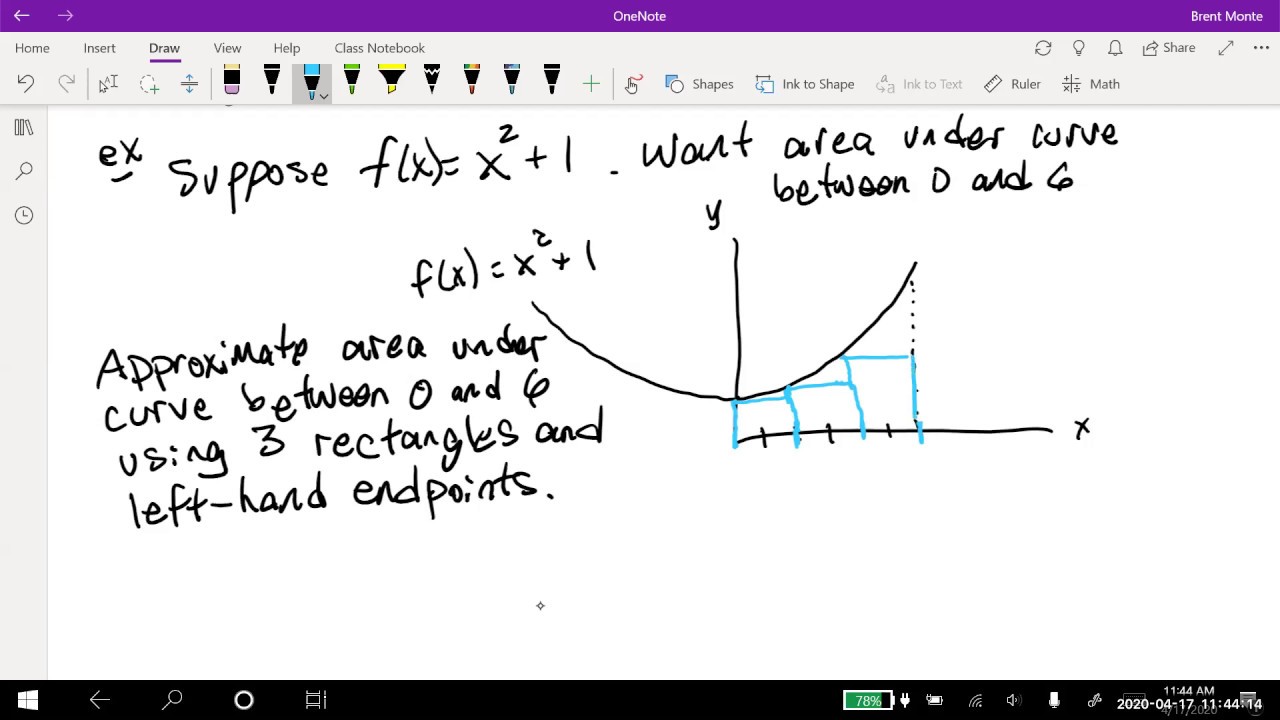
This paragraph transitions from arithmetic to algebraic and graphical representations of calculus concepts. It uses the idea of steps and slopes to explain how to calculate the total change in the function. The paragraph introduces the concept of delta y (the change in y) and delta x (the change in x), and how their ratio approaches the slope of the function. It also discusses the idea of taking limits as delta x approaches zero, which is a fundamental step in calculus.
🌟 The Limiting Process in Calculating Integrals
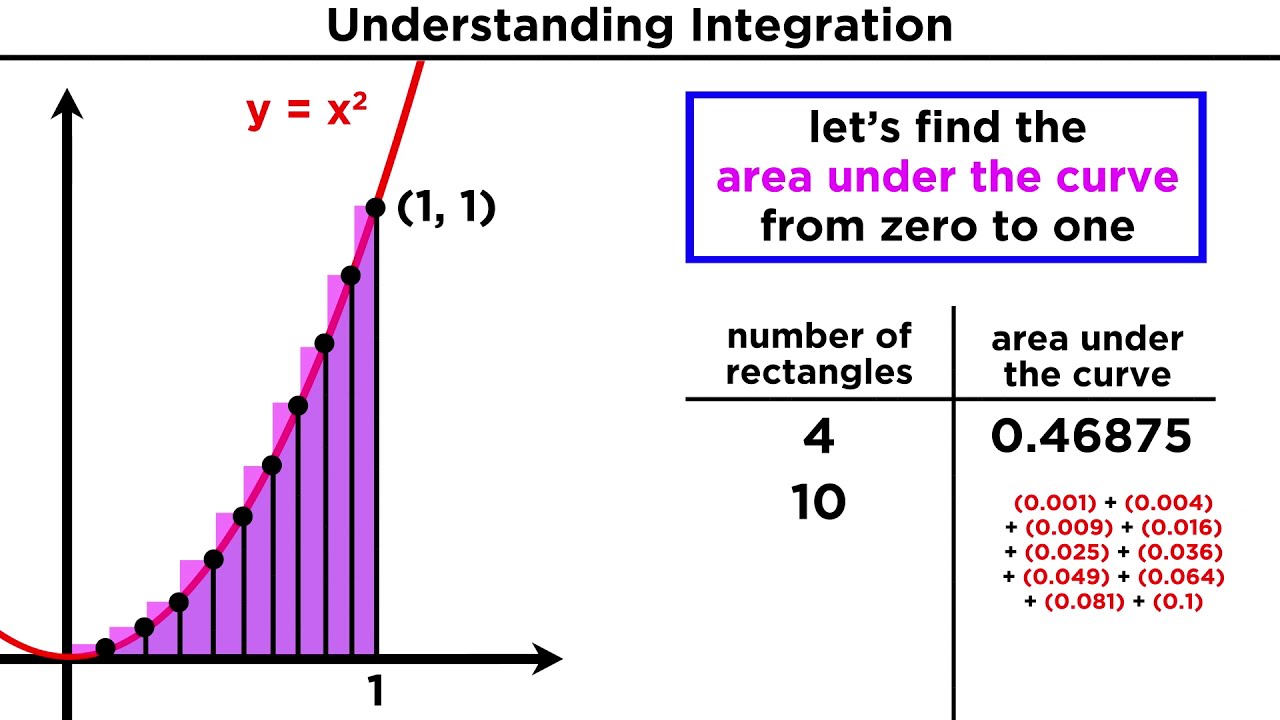
The fourth paragraph focuses on the limiting process involved in calculating integrals. It explains how as delta x becomes smaller, the sum of the slopes at different points approaches the actual function. The paragraph illustrates this concept with a practical example, showing how the integral of a function can be visualized as the area under a curve. It highlights the importance of the limit in refining the approximation of the integral to get the exact area.
🎓 Historical Context and the Power of Integration
This paragraph provides historical context by mentioning the contributions of mathematicians like Archimedes, Newton, and Leibniz to the field of calculus. It emphasizes the power of integration and how it allows us to move from the slope function back to the original function. The paragraph also discusses the process of integration using a specific example, showing how to approximate the area under a curve by summing the areas of rectangles and how this approximation improves as delta x becomes smaller.
📊 Visualizing the Integral and the Final Graph
The final paragraph discusses the visualization of the integral and the resulting graph of the function. It explains how the area under the slope curve represents the integral and how this can be used to find the original function. The paragraph concludes by summarizing the process of going from the slope function back to the height function, either by finding a function that has the given slope or by understanding the limiting process that involves taking the limit as delta x approaches zero.
Mindmap
Keywords
💡Calculus
💡Derivative
💡Integral
💡Slope
💡Height Function
💡Power Functions
💡Limits
💡Summation
💡Algebra
💡Inverse Process
💡Area Under the Curve
Highlights
The lecture introduces the concept of integral calculus, which is the reverse process of differentiation.
The process involves understanding the relationship between a function's height (y of x) and its slope (s of x).
When the function is a straight line, the slope is simply the rise over run.
For curved functions, the derivative (slope) is found by taking the limit as the distance across approaches zero.
The integral symbol represents the reverse process of finding the height (y of x) from the known slope (s of x).
The fundamental idea is to sum up the slopes (delta y's) to recover the original function's height.
The process involves taking individual steps and then taking smaller steps, eventually leading to continuous change.
The sum of delta y's over a series of steps equals the total change in y (y end minus y start).
Calculus involves dealing with the ratio of delta y over delta x, which approaches the derivative as delta x gets smaller.
The integral of a function is represented by the area under the curve of its derivative.
The process of finding the integral involves a limit where delta x approaches zero, turning the sum into an integral.
The lecture provides an example where the slope function s of x is 2 minus 2x, and the goal is to find the corresponding height function y of x.
By taking smaller and smaller steps (delta x), the estimated area under the curve becomes more accurate.
The area under the curve at x equals 1 is found to be 1, and at x equals 1/2, it is 3/4.
The lecture demonstrates that the function y of x that has the derivative 2 minus 2x is x squared minus x.
The final graph of the function shows a curve starting with a slope of 2, reaching a maximum height at x equals 1, and then descending.
The integral calculus process is shown to be a powerful tool for understanding the relationship between a function and its derivative.
The lecture concludes by emphasizing the importance of understanding the limiting process behind integration.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: