Who cares about topology? (Inscribed rectangle problem)
TLDRThe video explores the fascinating world of topology, highlighting an unsolved problem known as the inscribed square problem and a creative solution for a weaker version involving inscribed rectangles. It explains how by focusing on pairs of points on a closed loop and using a 3D graph, one can demonstrate the existence of an inscribed rectangle. The solution leverages the properties of a Möbius strip, showcasing the practical applications of topology in solving mathematical problems.
Takeaways
- 🌟 The video introduces an unsolved problem in topology known as the inscribed square problem, which questions whether every closed loop can have at least one inscribed square.
- 🔍 The presenter shares a personal connection to topology, highlighting its role in inspiring interest in mathematics through demonstrations like the Möbius strip and the concept of a single-sided surface.
- 📈 A key part of the solution to a weaker version of the problem involves focusing on pairs of points on the loop rather than individual points, using the properties of rectangles to establish relationships.
- 📊 A function is defined to encode the midpoint and distance information of pairs of points on the loop, mapping them to a 3D space to visualize the potential for an inscribed rectangle.
- 🔄 The video emphasizes the continuous nature of the function, which is crucial for demonstrating the existence of a collision where two distinct pairs of points map to the same spot in 3D space.
- 🔧 The concept of ordered and unordered pairs of points is explored, with the latter being essential for solving the problem, as it allows for the representation of all possible pairs without duplication.
- 🏠 The video describes the process of transforming a unit square into a torus for ordered pairs and a Möbius strip for unordered pairs, illustrating the continuous one-to-one association between points on these surfaces and pairs on the loop.
- 🧩 The Möbius strip's unique properties, particularly its ability to represent unordered pairs of points without duplication, become central to the solution for the inscribed rectangle problem.
- 🎓 The presenter underscores the practical applications of topology, showing that it's not just about abstract concepts but can be used to solve concrete problems like the inscribed rectangle problem.
- 🌐 The solution to the problem relies on the topological insight that the Möbius strip must intersect itself when mapped onto a 2D plane, which implies the existence of an inscribed rectangle on the loop.
- 🤓 The video concludes by encouraging viewers to appreciate the importance of topology and its role in problem-solving, as well as the significance of understanding the properties of shapes and surfaces.
Q & A
What is the main topic of the video?
-The main topic of the video is an unsolved problem in topology known as the inscribed square problem, along with an elegant solution to a weaker version of the problem and an introduction to the field of topology.
How did the speaker's interest in topology begin?
-The speaker's interest in topology began as a child when they were exposed to demonstrations involving shapes like the Möbius strip and topologists' views on objects like coffee mugs and donuts, which left them curious about how this relates to problem-solving in mathematics.
What is the inscribed square problem?
-The inscribed square problem asks whether it is always possible to find four points on any given closed loop in space that form a square. The problem is unsolved, meaning that there is no current mathematical proof to confirm or deny the existence of at least one inscribed square for every possible closed loop.
How does the video approach the unsolved problem?
-The video approaches the unsolved problem by discussing a weaker version of it, focusing on finding inscribed rectangles instead of squares. It presents a method that involves defining a function based on pairs of points on the loop and their properties to prove the existence of an inscribed rectangle.
What is the significance of the Möbius strip in the video?
-The Möbius strip is significant because it is used to represent unordered pairs of points on the loop. The video demonstrates that there is a continuous one-to-one association between these unordered pairs and points on the Möbius strip, which is crucial in solving the problem of finding inscribed rectangles.
How does the video explain the concept of ordered and unordered pairs of points?
-Ordered pairs have a specific first and second point (e.g., AB is different from BA), while unordered pairs do not consider the order (AB is the same as BA). The video uses the analogy of a unit square to explain ordered pairs and shows how to transition to unordered pairs by folding the square diagonally to represent the equivalence of all pairs with reversed order.
What is the role of the torus in the video's explanation?
-The torus is used to represent ordered pairs of points on the loop. It is derived from a square by gluing its opposite edges together in a specific way. The torus helps in understanding how pairs of points on a loop can be represented in a continuous 2D surface before moving on to the concept of unordered pairs and the Möbius strip.
How does the video connect the Möbius strip to the inscribed rectangle problem?
-The video connects the Möbius strip to the inscribed rectangle problem by showing that every point on the Möbius strip corresponds to a unique pair of points on the loop. It then uses the properties of the Möbius strip and its continuous association with the 3D graph defined by the midpoint and distance of pairs of points to prove that there must be at least one inscribed rectangle on any closed loop.
What is the key insight that leads to the solution of the inscribed rectangle problem?
-The key insight is that the Möbius strip, which represents unordered pairs of points on the loop, must intersect itself when mapped onto the 3D surface defined by the midpoint and distance of pairs of points. This intersection implies the existence of two distinct pairs of points with the same midpoint and distance, thus forming a rectangle.
Why is the solution to the inscribed rectangle problem considered elegant?
-The solution is considered elegant because it uses the properties of the Möbius strip and topological concepts to provide a beautiful and intuitive explanation for the existence of inscribed rectangles, without needing complex mathematical calculations.
What is the broader takeaway from the video regarding the field of topology?
-The broader takeaway is that topology, while seemingly abstract and focused on shapes and properties, has practical applications in problem-solving. It demonstrates how topological concepts like the Möbius strip and the torus can be used to tackle and gain insights into specific mathematical problems.
Outlines
🌟 Introduction to Topology and the Inscribed Square Problem
The video begins with an introduction to topology and the excitement around sharing mathematical concepts, particularly those related to shapes and their properties. The speaker reminisces about their childhood experiences with math and how topology, often demonstrated through a mobius strip or comparing a coffee mug to a donut, was used to spark interest. However, these demonstrations left the speaker questioning the practical applications of such math. The video aims to address this by discussing an unsolved problem known as the inscribed square problem, which asks whether every closed loop can have at least one inscribed square. The speaker then introduces a weaker version of the problem, inscribed rectangles, for which there is a beautiful solution involving a shift in focus from individual points to pairs of points on the loop.
📈 Defining a Function for Pairs of Points and its 3D Representation
The speaker explains a method to find inscribed rectangles by defining a function that takes pairs of points on a loop and outputs a point in 3D space, encoding the midpoint and distance information. The loop is considered to lie on the xy-plane, and for each pair of points, the midpoint is identified on the plane, with the distance between the points represented as height in the z-direction. This results in a surface that closely follows the loop. The function is continuous, meaning small changes in the input pair of points result in only slight changes in the output point. The goal is to demonstrate that this function has a collision, where two distinct pairs of points map to the same 3D point, implying the existence of an inscribed rectangle. The speaker then delves into the concept of ordered and unordered pairs of points and how they can be represented using a two-dimensional coordinate plane, leading to the idea of a torus representing all pairs of points on the loop.
🔄 From Ordered to Unordered Pairs: The Möbius Strip
The speaker continues the exploration of pairs of points by transitioning from ordered pairs, which consider the sequence of points, to unordered pairs, where the sequence does not matter. The challenge lies in representing unordered pairs in a unique way, which leads to the concept of a Möbius strip. The speaker describes a process of transforming a unit square into a Möbius strip by gluing its edges in a specific manner, with the diagonal fold being crucial for representing pairs where the points are the same. The Möbius strip is shown to have a continuous one-to-one association with unordered pairs of points on the loop, which is key to solving the inscribed rectangle problem. The speaker emphasizes the significance of the Möbius strip in understanding the problem and how its properties lead to the proof that an inscribed rectangle must exist for any closed loop.
🎉 The Proof and the Role of Topology
The video concludes with the speaker presenting the proof for the existence of an inscribed rectangle in any closed loop. By leveraging the continuous association between the Möbius strip and the 3D surface defined by the pairs of points, the speaker shows that the Möbius strip must intersect itself when mapped onto the surface, indicating the presence of two distinct pairs of points with the same midpoint and distance apart, thus forming a rectangle. The speaker reflects on the intuitive nature of the proof when considering the Möbius strip and acknowledges that a rigorous proof would require a deep understanding of topology. The speaker highlights the practical applications of topology and how it provides insights into solving concrete problems, encouraging appreciation for the field and its definitions.
Mindmap
Keywords
💡Topology
💡Inscribed Square Problem
💡Elegant Solution
💡Möbius Strip
💡Torus
💡Ordered and Unordered Pairs
💡Continuous Function
💡Collision Point
💡3D Space
💡Loop
💡Midpoint
Highlights
An unsolved problem and an elegant solution to a weaker version are discussed, showcasing the beauty of mathematics.
The video introduces the concept of topology and its relevance in solving mathematical problems.
The inscribed square problem is presented as an unsolved question in mathematics.
A method for finding inscribed rectangles is explained, despite the difficulty of the original inscribed square problem.
The solution involves a shift in focus from individual points to pairs of points on a loop.
A function is defined to encode midpoint and distance information of pairs of points on a loop.
The concept of a 3D graph is introduced to visualize the pairs of points.
The surface drawn in 3D space hugs the loop, providing insights into the problem.
The importance of the continuity of the function in the solution is emphasized.
The goal is to find a collision in the function, indicating a shared midpoint and equal distance between pairs of points.
The representation of pairs of points using a two-dimensional coordinate plane is discussed.
The process of straightening the loop and mapping it onto an interval is explained.
The torus is introduced as the natural shape for ordered pairs of points on the loop.
The Möbius strip is revealed as the natural shape for unordered pairs of points on the loop.
The continuous one-to-one association between unordered pairs of points on the loop and the Möbius strip is highlighted.
The inscribed rectangle problem is solved by demonstrating that the Möbius strip must intersect itself when mapped onto the 3D surface.
The solution showcases the practical applications of topology in solving concrete problems.
The video concludes by emphasizing the importance of understanding topology for solving mathematical problems.
Transcripts
Browse More Related Video
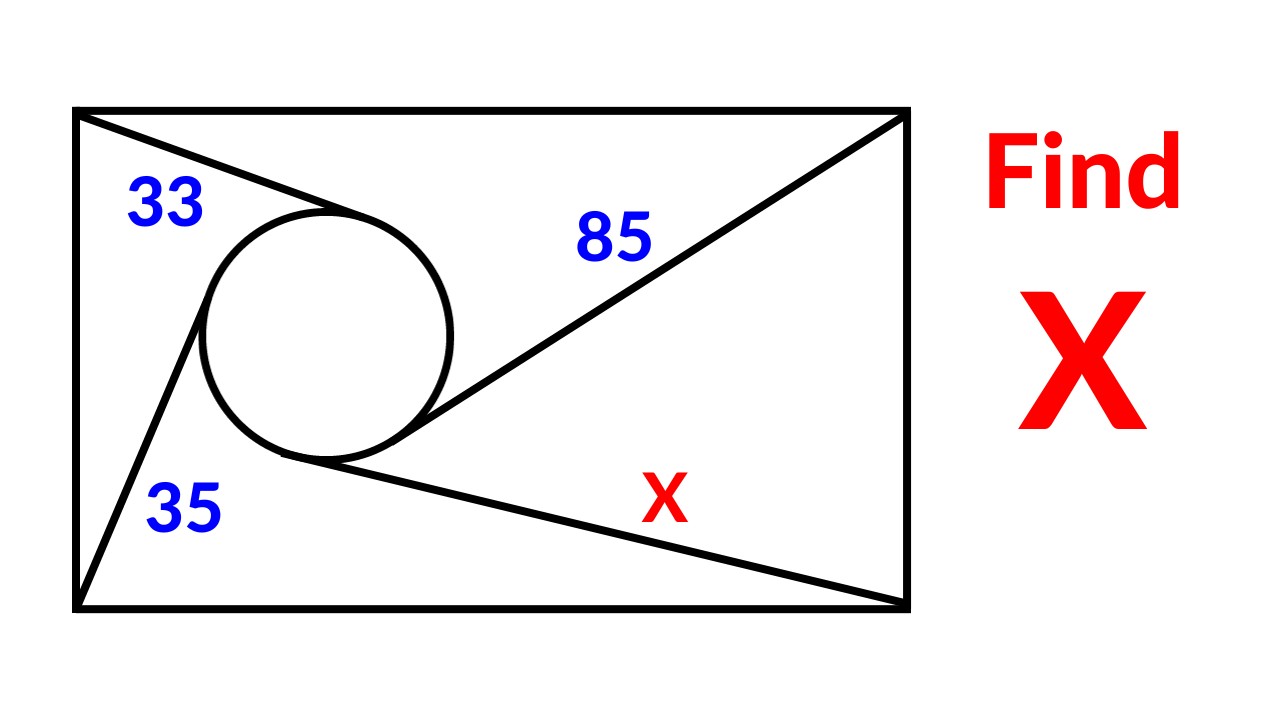
Hungary Math Olympiad Problem | Best Math Olympiad Problems | Geometry Problem
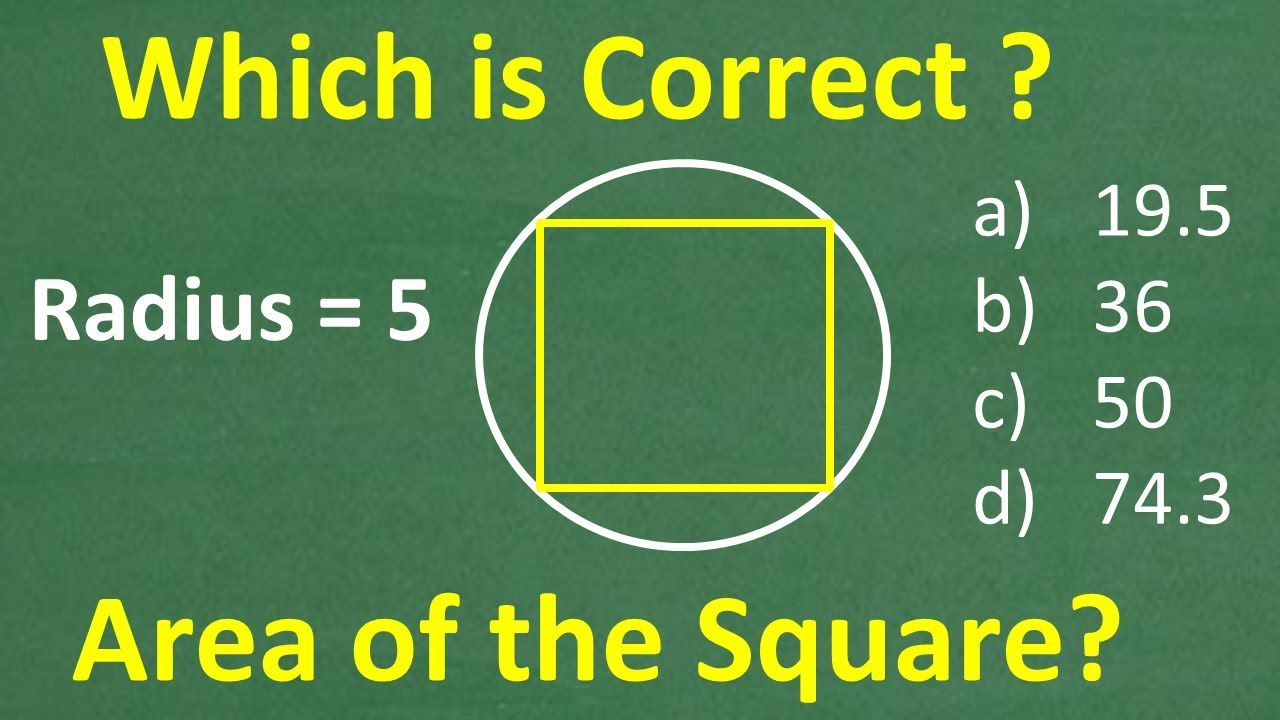
A square is inscribed in a circle with radius = 5, what is the area of the square?
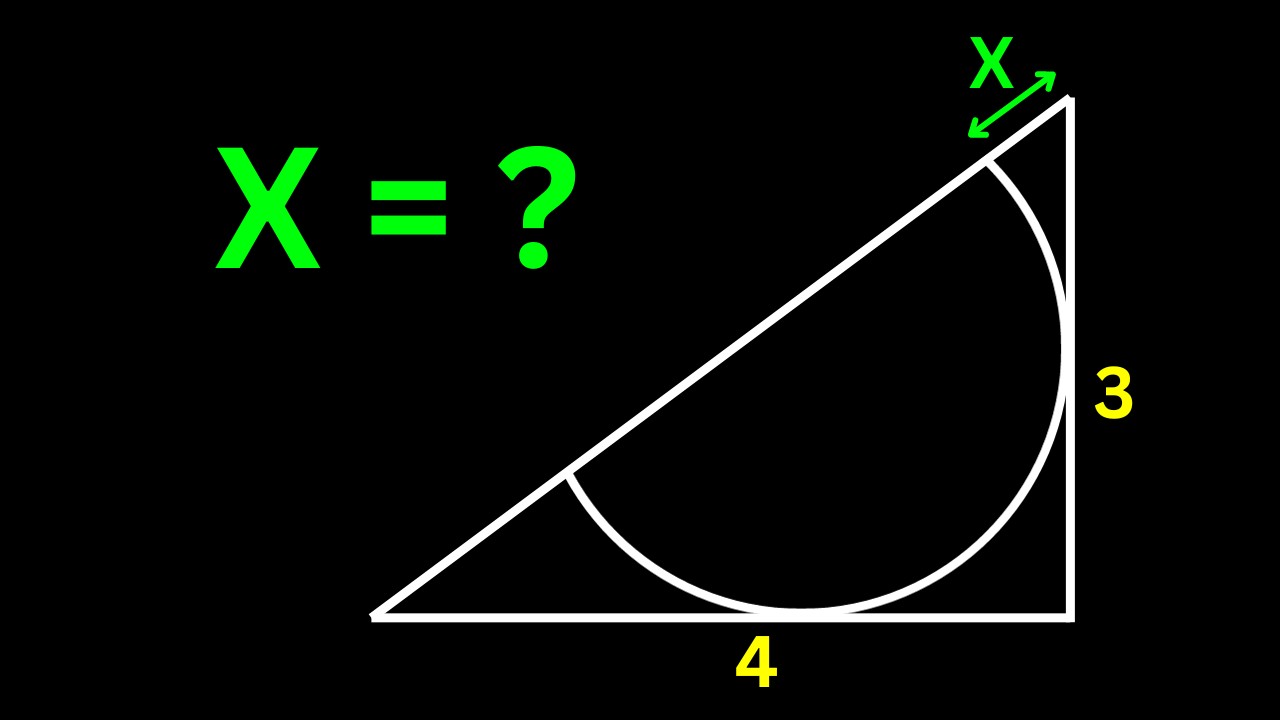
Canada Math Olympiad Problem | Best Math Olympiad Problems | Geometry
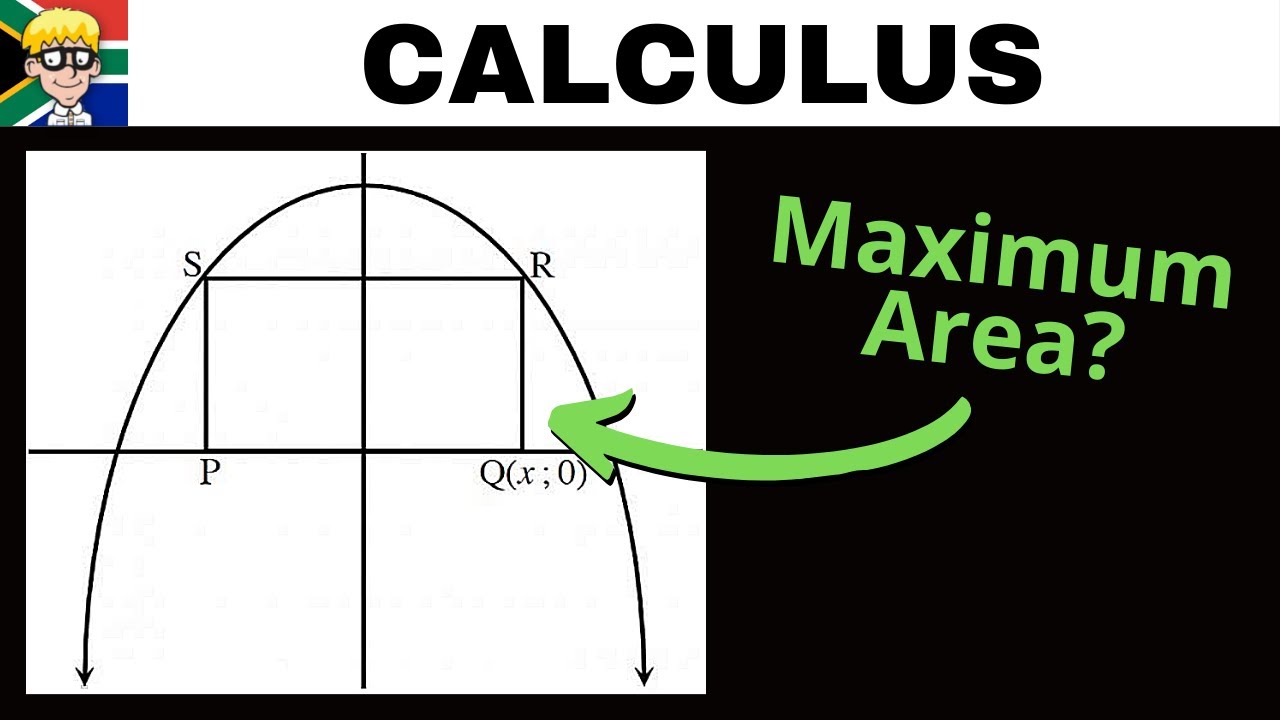
Optimisation Grade 12

Learn Topology in 5 minutes (joke video)
Special Right Triangles - 45 45 90 - Trigonometry & Geometry | SAT Math
5.0 / 5 (0 votes)
Thanks for rating: