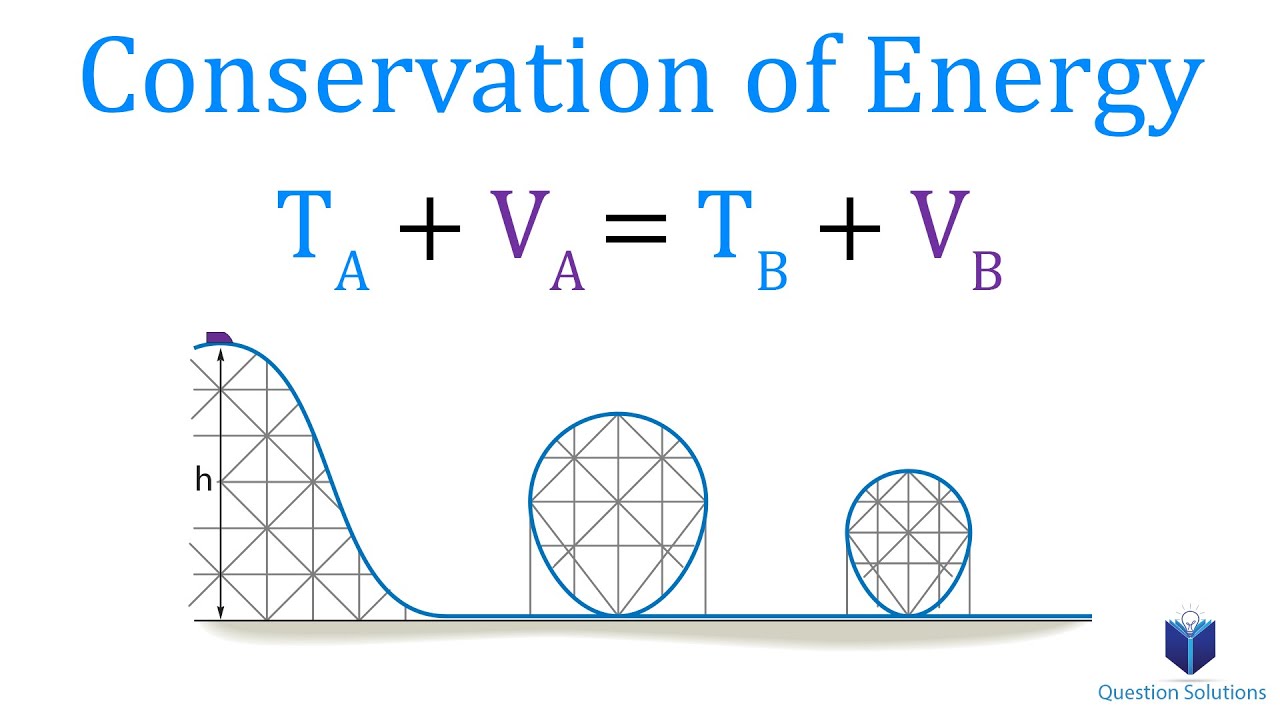
Potential Energy

Bozeman Science
19 Feb 201506:39
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, Mr. Andersen explores the concept of potential energy, emphasizing that it is energy due to position within a system and is dependent on conservative forces. He explains that lifting a crate gives it potential energy due to gravity, but sliding it across the floor does not. He covers three types of conservative forces: gravitational, mass-spring oscillators, and electric fields, providing equations and examples for calculating potential energy in each scenario. The video aims to clarify how potential energy is stored and retrieved in various physical systems.

Takeaways
  • πŸ“¦ Lifting an object, like a crate, against gravity gives it potential energy due to its position relative to the Earth.
  • 🚫 Sliding an object across the floor does not give it potential energy, as there is no conservative force involved.
  • 🌐 Potential energy is stored in a system only when conservative forces are at play, such as gravitational, spring, or electric fields.
  • πŸ”„ Conservative forces are those where the work done is independent of the path taken by the object.
  • πŸ“ˆ The potential energy stored in an object due to gravity is calculated as m*g*y, where m is mass, g is the acceleration due to gravity, and y is the height.
  • 🎯 The work done on an object lifted to a certain height can be fully recovered when the object is released, demonstrating the conservation of energy.
  • 🏹 In a mass-spring system, the potential energy stored is given by the formula 1/2*k*x^2, where k is the spring constant and x is the displacement.
  • πŸ”‹ The potential electric energy stored when a charge is moved within an electric field is calculated as the charge times the change in potential (voltage).
  • 🌌 An object in space does not have potential energy due to position because there is no gravitational field or other conservative forces acting on it.
  • πŸ”„ The path of energy storage and retrieval in conservative systems is cyclical, and the total potential energy remains constant regardless of the path taken.
  • πŸ“š Understanding the principles of potential energy and the role of conservative forces is crucial for analyzing and calculating energy in physical systems.
Q & A

  • What is potential energy in the context of the video?

    -Potential energy is the energy an object possesses due to its position within a system, and it is associated with conservative forces.

  • How does lifting a crate with a cable add potential energy to it?

    -Lifting a crate with a cable adds potential energy because the crate is raised against the Earth's gravitational field, and if the cable is cut, the crate will fall back to the ground, releasing the stored energy.

  • Why doesn't sliding a crate across the floor add potential energy to it?

    -Sliding a crate across the floor does not add potential energy because there are no conservative forces at play; the crate will not move back to its original position without external intervention.

  • What is a conservative force?

    -A conservative force is one where the work done on an object is independent of the path taken by the object. The total amount of work done to move an object within a conservative force field remains the same, regardless of the path chosen.

  • What are the three types of conservative forces discussed in the video?

    -The three types of conservative forces discussed are gravitational forces, mass-spring oscillators, and electric fields within a circuit.

  • How is gravitational potential energy calculated?

    -Gravitational potential energy is calculated using the formula m*g*Ξ”y, where m is the mass of the object, g is the acceleration due to gravity, and Ξ”y is the change in height of the object within the gravitational field.

  • What is the significance of the path in calculating work done by conservative forces?

    -The path is significant for non-conservative forces, as the work done depends on the path taken. However, for conservative forces, the work done is path-independent, and the total energy remains conserved regardless of the path.

  • How does the video illustrate the concept of work done by conservative forces?

    -The video uses the example of lifting an object and then letting it go to show that the work done on the object (in the form of potential energy) is returned when the object falls back down, demonstrating the conservation of energy in conservative forces.

  • What is the equation for potential energy in a mass-spring oscillator?

    -The equation for potential energy in a mass-spring oscillator is 1/2 * k * x^2, where k is the spring constant and x is the displacement of the mass from its equilibrium position.

  • How is potential electric energy calculated in a circuit?

    -Potential electric energy in a circuit is calculated using the formula Q*Ξ”V, where Q is the charge and Ξ”V is the change in voltage or potential across the circuit.

  • What is the main takeaway from the video regarding potential energy?

    -The main takeaway is that potential energy is stored in a system due to the position of objects within it, but only when conservative forces are involved. The video also emphasizes the importance of understanding how to quantitatively calculate potential energy in such systems.

Outlines
00:00
πŸ“š Introduction to Potential Energy

This paragraph introduces the concept of potential energy, specifically gravitational potential energy, by using the example of a crate being lifted and its potential to fall back to Earth. It explains that potential energy is energy due to position and is associated with conservative forces. The paragraph also sets the stage for discussing different types of conservative forces, such as gravitational fields, mass-spring oscillators, and electric fields with charges, and emphasizes that potential energy is stored when work is done by conservative forces.

05:01
πŸ”„ Calculating Gravitational Potential Energy and Conservative Forces

This paragraph delves into the calculation of gravitational potential energy using the formula mgy, where m is mass, g is the acceleration due to gravity, and y is the height. It provides a worked example of lifting an object 2 meters high and calculates the potential energy as -39 joules. The concept of conservative forces is further explored, explaining that the work done is path-independent, and the same amount of energy can be recovered regardless of the path taken. The paragraph also touches on the potential energy in a mass-spring system and the potential electric energy in a circuit with charges.

Mindmap
Keywords
πŸ’‘Potential Energy
Potential energy is the energy an object possesses due to its position relative to other objects. In the context of the video, it is energy stored in an object because of its position within a gravitational field or due to its interaction with conservative forces such as a spring. The video explains that potential energy is released when an object is allowed to move back to its original position, as in the case of lifting a crate and then letting it fall back to Earth.
πŸ’‘Conservative Forces
Conservative forces are those that do not dissipate energy as heat or other forms of non-mechanical work. They are forces where the work done on an object is independent of the path taken and only depends on the initial and final positions. This means that the energy put into the system is conserved and can be fully recovered. In the video, gravity, spring force, and electric fields are cited as examples of conservative forces.
πŸ’‘Work
Work, in the context of physics, is the measure of energy transfer that occurs when an object is moved by applying a force along a displacement. The video emphasizes that work must be done by a conservative force to store potential energy. It is calculated as the product of the force applied and the displacement in the direction of the force.
πŸ’‘Gravitational Potential Energy
Gravitational potential energy is the energy an object has due to its elevated position in a gravitational field. The higher the object is lifted, the greater its gravitational potential energy. It is calculated using the formula mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height above the reference point.
πŸ’‘Mass-Spring Oscillator
A mass-spring oscillator is a simple mechanical system consisting of a mass attached to a spring. It is an example of a system that stores potential energy when the spring is compressed or stretched. The potential energy in a mass-spring system is given by the formula 1/2 kx^2, where k is the spring constant and x is the displacement from the equilibrium position.
πŸ’‘Electric Potential Energy
Electric potential energy is the energy stored in an electric field, specifically when a charge is placed within it. This form of potential energy is related to the electric potential difference (voltage) and the amount of charge. It is calculated using the formula EPE = qV, where q is the charge and V is the potential difference.
πŸ’‘Path Independence
Path independence refers to the property of conservative forces where the total work done to move an object from one point to another is the same, regardless of the path taken. This is a key characteristic of conservative forces, indicating that the energy stored in a system is conserved and can be fully recovered.
πŸ’‘Non-Conservative Forces
Non-conservative forces are those that do not satisfy the path independence property. They dissipate mechanical energy, converting it into other forms of energy, such as heat. Unlike conservative forces, the work done by non-conservative forces depends on the path taken, and not all of the energy put into the system can be recovered.
πŸ’‘Energy Conservation
Energy conservation is the principle that the total energy in an isolated system remains constant, though it may change forms. In the context of the video, it is illustrated that when only conservative forces are at play, the total mechanical energy (kinetic plus potential) remains constant, as potential energy is converted to kinetic energy and vice versa.
πŸ’‘System
In physics, a system is a set of objects or a region of space that is being studied, and which is separated from its surroundings by a defined boundary. The video discusses how potential energy is stored within a system due to the position of its constituent objects and their interactions with conservative forces.
πŸ’‘Position
In the context of the video, position refers to the location of an object within a system or a field, such as a gravitational or electric field. The position of an object is crucial in determining the amount of potential energy it possesses, especially when conservative forces are involved.
Highlights

Potential energy is defined as energy due to position.

Lifting a crate and adding potential energy is an example of work done on the object.

Potential energy is not created by non-conservative forces, such as friction.

Conservative forces include gravitational fields, mass-spring oscillators, and electric fields with charges.

The work done on an object by conservative forces is path-independent.

Gravitational potential energy can be calculated using the formula mgy, where m is mass, g is the gravitational field strength, and y is the height.

An object lifted 2 meters in a gravitational field has 39 joules of potential energy.

The path of energy transfer in a conservative system does not affect the total potential energy.

A mass-spring oscillator stores potential energy that can be calculated using the formula 1/2 kx^2, where k is the spring constant and x is the displacement.

A baseball attached to a spring with a spring constant of 125 N/m and displaced by 0.22 meters has 3.0 joules of potential energy.

Electric potential energy in a circuit can be calculated using the formula QV, where Q is the charge and V is the voltage.

A charge of 1 coulomb in a 1.5-volt battery has -1.5 joules of potential energy.

Potential energy is conserved in a system with conservative forces, meaning it can be fully recovered.

The video explains the concept of potential energy and its relation to conservative forces in a clear and educational manner.

Understanding potential energy is crucial for solving problems in AP Physics.

The video provides practical examples and equations for calculating potential energy in various physical systems.

Transcripts

Browse More Related Video

Conservation of Energy (Learn to solve any problem)

How to Calculate Work in Physics

Potential Energy EXPLAINED in 5 Levels: What Level Are YOU? Beginner - Advanced Classical (Parth G)

Kinetic Energy

Internal Energy

6. Capacitors

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsPotential EnergyConservative ForcesGravitational FieldMass Spring OscillatorElectric ChargesEnergy ConservationAP PhysicsEducational ContentMr. Andersen