7. Trial and Error Searching
TLDRThis script delves into trial and error searching, an essential method for computers to solve problems that aren't straightforward. It introduces root-finding through trial and error, explaining the concept using the analogy of a spaniel searching for a ball. The discussion covers two primary algorithms: the Bisection Method, a reliable but slower approach, and the Newton-Raphson Method, which is faster but potentially less robust. The script also includes practical exercises involving quantum mechanics to apply these algorithms, emphasizing the importance of numerical methods in finding solutions to complex equations without analytical forms.
Takeaways
- 🔍 The script discusses trial and error searching, a method where computers make intelligent guesses to find solutions, akin to a spaniel searching for a ball.
- 📚 It introduces the concept of root finding by trial and error, which involves finding when an equation equals zero, a fundamental problem in science and engineering.
- 🔧 The script explains that equations not in the standard form can be manipulated by creating a new function that represents the difference between two functions to be solved.
- 🎯 The bisection algorithm is introduced as a simple but reliable method for finding roots, which works by repeatedly bisecting an interval where a sign change is known to occur.
- 📉 The bisection method is illustrated with a graphical example of a parabola, demonstrating how the interval is narrowed down until the root is approximated closely enough.
- 🤖 The Newton-Raphson algorithm is presented as a faster but less robust alternative to the bisection method, which uses the tangent of the function to make more aggressive guesses towards the root.
- 📈 The Newton-Raphson method is shown to potentially fail if the function has local minima or maxima, which can cause the algorithm to diverge to infinity or loop infinitely.
- 📝 The script emphasizes the importance of handling singularities and infinities in functions when using numerical methods, as they can disrupt the search for roots.
- 🧩 The exercises provided in the script involve applying the bisection and Newton-Raphson methods to solve a transcendental equation related to quantum mechanics, specifically finding energy levels of a particle in a quantum well.
- 📊 The importance of plotting functions to understand their behavior, especially near singularities, is highlighted as a way to better apply numerical methods and interpret results.
- 🔬 The script encourages exploration of the effects of changing parameters in the equation, such as the depth of the potential well, to observe changes in the number of possible solutions.
Q & A
What is the main topic of discussion in the script?
-The main topic of the script is trial and error searching, particularly as it applies to root-finding in computational science.
What is a 'trial' in the context of trial and error searching?
-In trial and error searching, a 'trial' refers to an attempt or guess made by the computer to find a solution, similar to the initial circling a spaniel does when searching for a ball.
What does 'error' signify in trial and error searching?
-In this context, 'error' refers to the situation when a trial does not result in finding the solution, prompting the computer to make a different trial.
What is a root of an equation in mathematical terms?
-A root of an equation is the value of the variable that makes the equation equal to zero, i.e., when f(x) = 0.
How can the bisection algorithm be described in simple terms?
-The bisection algorithm is a method for finding the root of a function by repeatedly dividing the interval in half and selecting the midpoint as a new guess, based on whether the function changes sign in that interval.
What is the significance of the Newton-Raphson algorithm mentioned in the script?
-The Newton-Raphson algorithm is a more sophisticated root-finding method that uses the tangent line to the function at the current guess to find a new guess, which can converge to the root more quickly than the bisection method.
Why might the Newton-Raphson method fail to find a root?
-The Newton-Raphson method might fail if the function has a local minimum or maximum, or if the function's derivative is zero, causing the method to produce an infinite or undefined next guess.
What is the purpose of the exercises mentioned in the script?
-The exercises are designed to give practical experience in using the bisection and Newton-Raphson methods to solve a transcendental equation related to quantum mechanics, specifically finding the energy levels of a particle in a quantum well.
What is a transcendental equation, and why is it difficult to solve?
-A transcendental equation is an equation that involves a variable in a non-polynomial function, such as an exponential or trigonometric function. It is difficult to solve because it often lacks an analytic solution and requires numerical methods.
How can one determine if a function has multiple roots?
-One can determine if a function has multiple roots by analyzing its behavior over a range of values, looking for sign changes or by using numerical methods to approximate roots and then checking if the function equals zero at those points.
What is the role of plotting in solving transcendental equations?
-Plotting helps visualize the function and identify where it may cross the x-axis, indicating potential roots. It also helps in understanding the behavior of the function, such as the presence of singularities, which can affect numerical methods.
Outlines
🔍 Introduction to Trial and Error Searching
The paragraph introduces the concept of trial and error searching, a method where the computer makes intelligent guesses to find solutions to problems, akin to how a spaniel searches for a ball. The analogy of a spaniel making circles to find a ball is used to illustrate the iterative process of trial and error. The main idea is to find the roots of an equation, which is a fundamental problem in science and engineering. The process involves making a guess, evaluating its accuracy, and then refining the guess based on the error. The goal is to find when a function equals zero within a certain tolerance level, which is a practical approach given the limitations of floating-point arithmetic.
📈 The Bisection Algorithm for Root Finding
This paragraph delves into the bisection algorithm, a simple yet reliable method for finding the roots of a function. The algorithm is based on the premise that if a function changes sign over a certain interval, a root must exist within that interval. The process involves iteratively narrowing down the interval by bisecting it and selecting the midpoint as the new guess. The algorithm checks the sign of the function at the new guess and adjusts the interval accordingly. While the bisection method is not the fastest, it is guaranteed to converge to a solution if the function changes sign within the initial interval.
🌟 Newton-Raphson Method: A More Efficient Approach
The paragraph introduces the Newton-Raphson method, a more advanced and typically faster method for finding roots of a function compared to the bisection algorithm. This method uses the concept of drawing a tangent to the function at a guessed point and then finding where this tangent crosses the x-axis, which becomes the new guess. The process is repeated until the desired level of accuracy is achieved. The Newton-Raphson method is highlighted as being quicker but potentially less robust, as it can fail if the function has local minima or maxima, or if the function's derivative is zero, leading to an infinite slope.
📚 Analyzing the Newton-Raphson Method Mathematically
The paragraph provides a mathematical explanation of the Newton-Raphson method, detailing how to use a Taylor expansion to approximate the function near the root and then solve for the correction needed to improve the guess. The process involves using the first two terms of the Taylor expansion and solving for the unknown correction, which is then used to update the guess. The paragraph also discusses potential issues with the method, such as the function's derivative being zero, which would require a more intelligent guess to avoid infinite results.
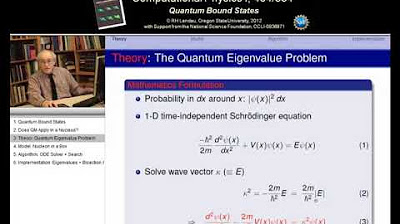
🧪 Practical Application: Solving Quantum Bound States Problem
This paragraph presents a practical application of the trial and error methods discussed, specifically focusing on finding quantum bound states within a potential well. The problem involves solving a transcendental equation that has no analytical solution but can be solved numerically. The paragraph suggests using the bisection algorithm to find an initial solution and then using the Newton-Raphson method to refine the solution. It also mentions the importance of dealing with singularities in the function and suggests transforming the equation to avoid issues with the search algorithms.
🚀 Further Exploration with Newton-Raphson and Physical Insights
The final paragraph encourages further exploration of the Newton-Raphson method by applying it to the quantum bound states problem and comparing its efficiency with the bisection algorithm. It also suggests experimenting with different depths of the potential well by changing a constant in the equation to observe the effect on the energy levels and the number of possible solutions. The paragraph concludes with an invitation to engage with the material through computer programming and numerical experimentation, emphasizing the exploratory nature of the task.
Mindmap
Keywords
💡Trial and Error Searching
💡Root Finding
💡Bisection Algorithm
💡Newton-Raphson Method
💡Transcendental Equation
💡Quantum Bound States
💡Tangent Function
💡Singularity
💡Numerical Methods
💡Artificial Intelligence
💡Precision and Tolerance
Highlights
Introduction to trial and error searching, a method where computers perform tasks not immediately obvious, involving guesswork and learning from errors.
Comparison of trial and error searching to a spaniel searching for a ball, emphasizing the iterative process of making larger or smaller circles to find the target.
Root finding by trial and error as a basic problem in computing science, representing the solution to many scientific and engineering problems.
Explanation of how to handle equations not in the standard form by creating a new function that equates to zero.
The importance of making intelligent guesses in trial and error methods, rather than random guesses, to avoid leading astray.
The concept of ending the search when the function equals zero within a certain level of precision or tolerance.
Incorporating a worst-case scenario into computations, such as quitting the routine if too many guesses are made without success.
The trial and error method as an example of artificial intelligence, where the computer adapts and makes decisions based on outcomes.
Introduction of the bisection algorithm, a simple and reliable method for finding the root of a function by continually bisecting the interval.
The requirement for the bisection algorithm to know the function changes sign within a certain region to ensure finding a zero.
The geometric interpretation of the bisection algorithm, visualizing the iterative process of narrowing down the interval to find the root.
The Newton-Raphson algorithm as a more sophisticated and faster method for root finding, with a geometric interpretation involving tangent lines.
The potential failure of the Newton-Raphson method due to local minima or maxima, sending the search to infinity.
Strategies to avoid failure in the Newton-Raphson method, such as taking partial steps and watching for infinite loops.
The analytical process of the Newton-Raphson method, involving fitting a tangent to the function and solving for when it crosses zero.
The importance of numerically evaluating the derivative in the Newton-Raphson method and the technique to approximate it.
Exercises involving quantum bound states and the application of trial and error methods to solve transcendental equations in quantum mechanics.
The use of bisection.java or similar programs to solve the given quantum mechanics problem, emphasizing the practical application of the discussed algorithms.
The challenge of dealing with singularities in transcendental equations and the strategy of transforming the equation to avoid them.
Further exploration of the problem by changing the depth of the potential well and observing the effect on the energy levels and number of solutions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: