Finding Taylor's Series | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRIn this educational video, Professors Jerison and Miller guide students through the computation of Taylor series for three distinct functions: the hyperbolic cosine, 2 times sine of x times cosine of x, and x times the logarithm of (1 - x cubed). The professors employ various techniques, including direct formula application, differentiation, and trigonometric identities, to derive the series. The video emphasizes the similarities between regular and hyperbolic trigonometric functions and demonstrates the utility of power series in mathematical analysis.
Takeaways
- 📚 The video script is a recitation on Taylor series, focusing on computing the series for three specific functions.
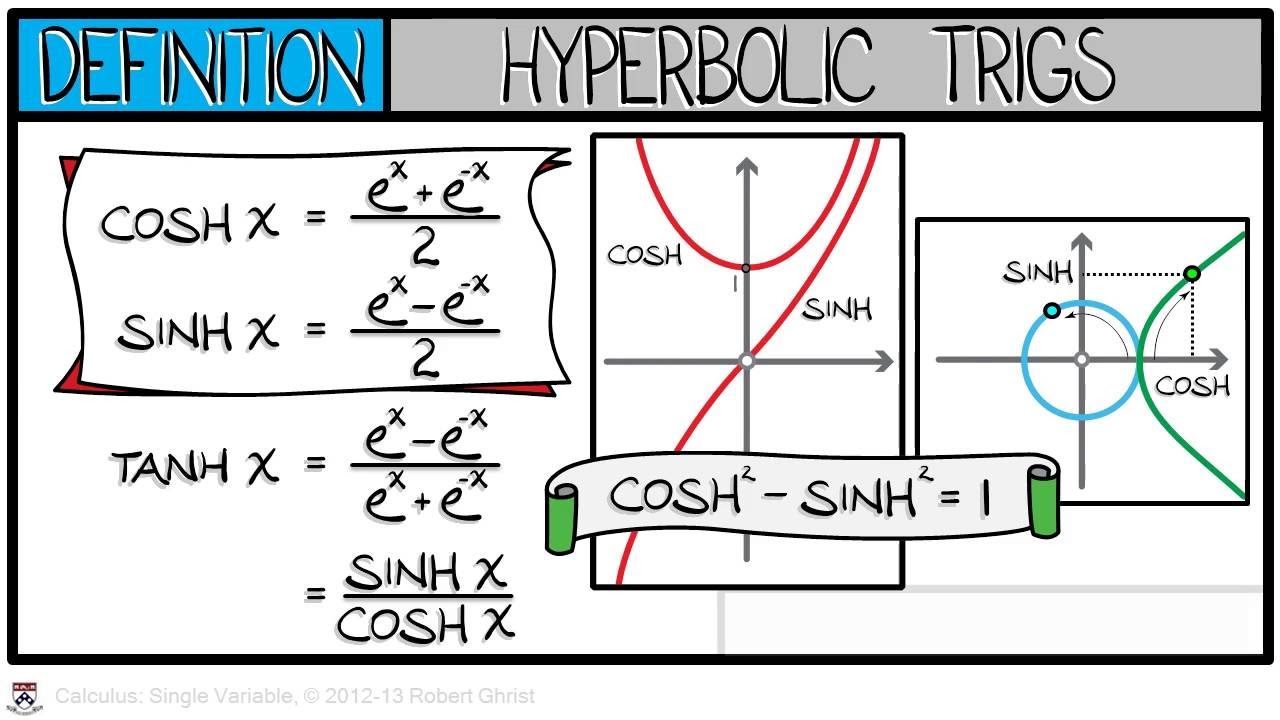
- 🔍 The first function discussed is the hyperbolic cosine, cosh(x), which can be expressed using exponential functions.
- 📈 The method for finding the Taylor series of cosh(x) involves recognizing its derivatives and simplifying the series of e^x and e^-x.
- 🧩 The Taylor series for cosh(x) is derived by adding the series of e^x and e^-x, with the odd terms canceling out, resulting in a series similar to e^x but with only even powers of x.
- 📉 The second function is 2 * sin(x) * cos(x), which can be simplified using trigonometric identities to sin(2x).
- 🌟 The Taylor series for 2 * sin(x) * cos(x) is obtained by substituting 2x into the known series for sin(x), leveraging the properties of sine and cosine functions.
- 📝 The third function is x * ln(1 - x^3), which requires understanding the Taylor series for ln(1 + x) and making a substitution.
- 🔑 The Taylor series for ln(1 - x^3) is found by substituting -x^3 into the series for ln(1 + x), adjusting for the change in the function.
- 🔍 For x * ln(1 - x^3), the series is obtained by multiplying the series for ln(1 - x^3) by x, simplifying the expression step by step.
- 📘 The script emphasizes the use of different techniques such as direct computation, substitution, and leveraging known identities to compute Taylor series.
- 🔄 The recitation concludes by summarizing the methods used for each function and the resulting power series, highlighting the connection between regular and hyperbolic trigonometric functions.
Q & A
What is the topic of the video script?
-The topic of the video script is the computation of Taylor series for certain mathematical functions, specifically the hyperbolic cosine, the product of sine and cosine, and a function involving the logarithm.
What is the first function mentioned in the script for which the Taylor series is computed?
-The first function mentioned is the hyperbolic cosine function, denoted as cosh(x).
How is the hyperbolic cosine function expressed in terms of exponential functions?
-The hyperbolic cosine function is expressed as \( e^x + e^{-x} \) divided by 2.
What is the second function discussed in the script, and how is it related to a known trigonometric identity?
-The second function is \( 2 \sin(x) \cos(x) \), which is recognized as the sine of 2x using the trigonometric identity for sine of a double angle.
What is the third function for which the Taylor series is computed, and what is its significance?
-The third function is \( x \ln(1 - x^3) \), which is significant because it involves a logarithmic function and requires a substitution to compute its Taylor series.
How are the derivatives of the hyperbolic cosine and hyperbolic sine related?
-The derivative of the hyperbolic cosine is the hyperbolic sine, and the derivative of the hyperbolic sine is the hyperbolic cosine again.
What is the general form of the Taylor series for the exponential function e^x?
-The general form of the Taylor series for e^x is \( \sum_{n=0}^{\infty} \frac{x^n}{n!} \).
How does the script simplify the computation of the Taylor series for cosh(x) by using the series for e^x and e^(-x)?
-The script simplifies the computation by adding the series for e^x and e^(-x), factoring out 1/2, and observing that the odd terms cancel out, leaving only the even terms doubled.
What is the summation notation for the Taylor series of the hyperbolic cosine function?
-The summation notation for the Taylor series of cosh(x) is \( \sum_{n=0}^{\infty} \frac{x^{2n}}{(2n)!} \).
How does the script suggest computing the Taylor series for 2 sine x cosine x using trigonometric identities?
-The script suggests recognizing 2 sine x cosine x as sine of 2x and then substituting 2x into the known Taylor series for sine x to compute the series for sine of 2x.
What substitution is made in the script to simplify the computation of the Taylor series for x ln(1 - x^3)?
-The substitution made is to recognize ln(1 - x^3) as a transformation of ln(1 + x) by substituting -x^3 for x, and then multiplying the resulting series by x.
What are the techniques used in the script to compute the Taylor series for the given functions?
-The techniques used include direct computation using known formulas, recognizing and applying trigonometric identities, and using substitution and multiplication by a polynomial for logarithmic functions.
Outlines
📚 Introduction to Taylor Series Examples
The script begins with an introduction to the topic of Taylor series, referencing previous lessons by Professor Jerison and Professor Miller. The lecturer presents three new functions to explore: the hyperbolic cosine (cosh x), the product of sine and cosine (2 * sin(x) * cos(x)), and a logarithmic function (x * ln(1 - x^3)). The audience is encouraged to pause and attempt the calculations before continuing with the video for a collaborative explanation. The first function, cosh x, is defined in terms of exponential functions and is simplified using the derivatives of hyperbolic functions and known Taylor series for e^x and e^-x, resulting in a series that resembles the Taylor series for cos x but with only even terms.
🔍 Deriving the Taylor Series for Trigonometric and Logarithmic Functions
The second paragraph delves into the process of deriving the Taylor series for the given functions. For the hyperbolic cosine, the method involves leveraging the simplicity of exponential function derivatives. The series for cosh x is shown to be a subset of the e^x series with only even powers of x. The lecturer then moves on to the product of sine and cosine, which can be simplified using trigonometric identities to recognize it as sin(2x). The Taylor series for sin(2x) is derived by substituting 2x into the known series for sin(x). Lastly, the logarithmic function x * ln(1 - x^3) is tackled by relating it to the known series for ln(1 + x), with a substitution to account for the negative sign and the cubic term. The resulting series for the logarithmic function involves powers of x that are multiples of four, with alternating signs.
📘 Conclusion of the Recitation on Power Series
In the final paragraph, the lecturer wraps up the recitation by summarizing the techniques used to compute the power series for the three functions. The methods included direct substitution using known power series, leveraging trigonometric identities for simplification, and applying the product rule for derivatives. The summary emphasizes the successful application of these techniques to derive the Taylor series for the given functions, providing a clear understanding of how to approach similar problems.
Mindmap
Keywords
💡Taylor series
💡Hyperbolic cosine (cosh x)
💡Sine and Cosine functions
💡Product rule
💡Trigonometric identities
💡Logarithm function
💡Substitution
💡Factorial
💡Power series
💡Differentiation
💡Summation notation
Highlights
Introduction to recitation on Taylor series and their manipulations.
Three new examples of functions with nice Taylor series computations: cosh x, 2sin(x)cos(x), and x*ln(1-x^3).
Cosh x defined as (e^x + e^-x) / 2, highlighting its relation to exponential functions.
Derivatives of hyperbolic cosine and sine are easily understood due to the properties of exponential functions.
Taylor series for e^x and e^-x derived using substitution and simplification.
Simplification of cosh x's Taylor series by elimination of odd terms, resulting in a series similar to e^x.
Summation notation for the Taylor series of cosh x presented.
Connection between the Taylor series of cosh x and the regular cosine function.
Exploration of 2sin(x)cos(x) as a product of Taylor series for sine and cosine.
Alternative approach to finding the Taylor series for 2sin(x)cos(x) using trigonometric identities.
Identification of 2sin(x)cos(x) as sine of 2x, simplifying the computation of its Taylor series.
Taylor series for sine of 2x derived by substituting 2x into the sine x series.
Introduction of x*ln(1-x^3) and its simplification by separating the polynomial and logarithmic parts.
Relation of ln(1-x^3) to the known series of ln(1+x) through substitution.
Derivation of ln(1-x^3)'s Taylor series by applying the series of ln(1+x) with a cubic substitution.
Final expression for x*ln(1-x^3)'s Taylor series by multiplying the derived logarithmic series by x.
Summary of techniques used in the recitation: direct computation, substitution, and multiplication by polynomials.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: