Related Rates Day 2
TLDRThis educational video script explores related rates problems involving rates of change. The instructor discusses three scenarios: reeling in a fish under a bridge, a man walking away from a light pole casting a shadow, and water filling a triangular trough. Using trigonometric functions and derivatives, the script demonstrates how to find rates of change for angles, distances, and water levels, providing step-by-step solutions to these classic calculus problems.
Takeaways
- 🎣 A fish is being reeled in from a bridge 16 feet above the water, and the angle between the line and the water is to be determined.
- 🔄 The fish is being reeled in at a rate of 2 feet per second, making the rate of change of the line length negative.
- 📐 The problem involves a right triangle, with the bridge height as one leg and the line length as the hypotenuse.
- 🧮 Using the tangent function, the relationship between the angle, the height, and the hypotenuse is established.
- ⏲️ The derivative of the tangent function is taken with respect to time to find the rate of change of the angle.
- 🧊 When the line length is 20 feet, the specific rates and angles are calculated.
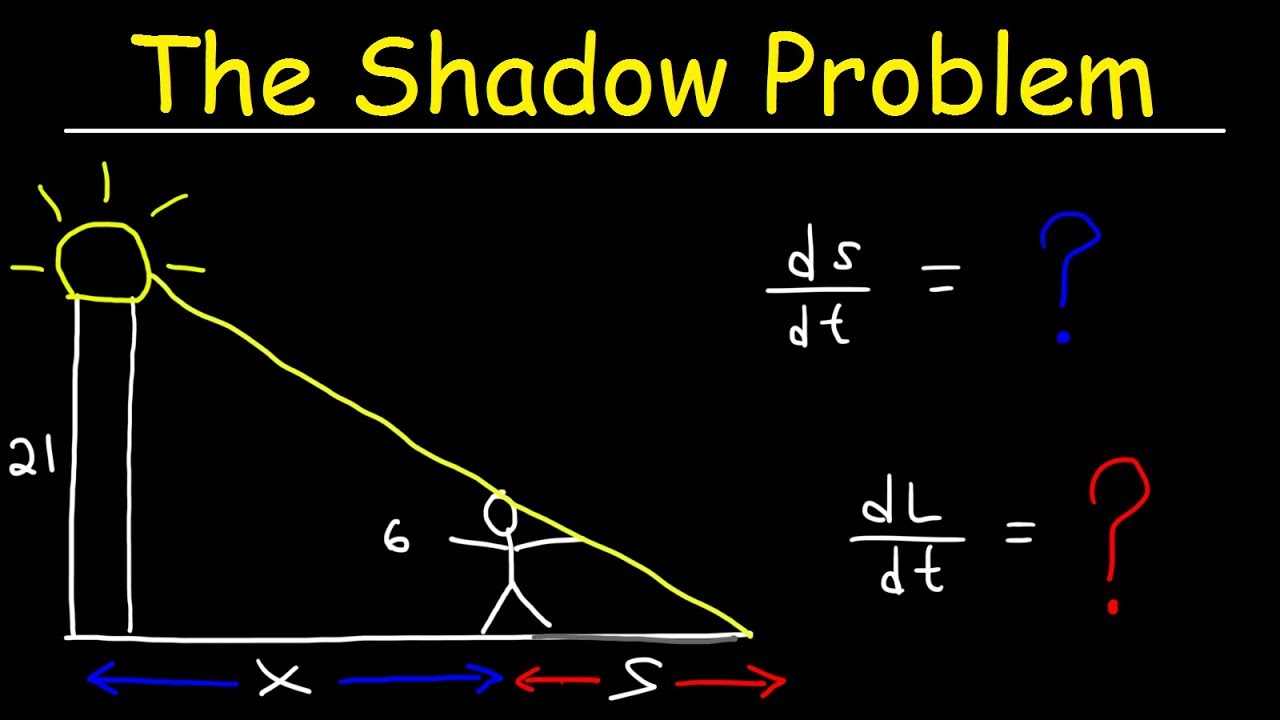
- 🏃 Another example involves a person walking away from a light pole and determining the rate at which the tip of his shadow moves.
- 🔺 Similar triangles are used to relate the height of the pole, the person, and the lengths of the shadows.
- 📈 The derivatives of these lengths are taken to find the rates of change in the shadow's tip and overall length.
- 🚰 A trough problem is presented where water is being pumped in, and the rate of the water level rise is calculated using volume equations.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is related rates problems, specifically involving the rate of change of angles and lengths in various scenarios such as a fish being reeled in, a person walking away from a light pole, and water being pumped into a trough.
What is the initial setup described for the fish being reeled in scenario?
-The initial setup for the fish being reeled in scenario involves a fish being reeled in with a line attached to it, a bridge 16 feet above the water, and the angle between the line and the water surface being denoted as theta.
What trigonometric function is used to relate theta, the angle, and the bridge height?
-The tangent function is used to relate theta and the bridge height, where the tangent of theta is equal to the opposite side (16 feet) divided by the hypotenuse (the length of the line, denoted as X).
How is the rate of change of the angle theta calculated?
-The rate of change of the angle theta (dθ/dt) is calculated using the derivative of the tangent function with respect to time, which involves the chain rule and results in dθ/dt = (-16/x^2) * (dx/dt).
What is the rate at which the fish is being reeled in?
-The fish is being reeled in at a rate of 2 feet per second, which is represented as dx/dt = -2.
What is the scenario described for the person walking away from a light pole?
-The scenario involves a person who is 6 feet tall walking away from a 16-foot tall light pole, with the tip of his shadow and his feet being the points of interest.
How are similar triangles used to solve the light pole problem?
-Similar triangles are used by setting up a proportion between the heights and distances of the triangles formed by the person, the light pole, and the shadow, which helps in deriving the relationship between the variables.
What is the rate of change of the tip of the shadow's position when the person is walking away?
-The rate of change of the tip of the shadow's position (dx/dt) is calculated to be 8 feet per second when the person is walking away at a rate of 5 feet per second.
What is the scenario described for the water being pumped into the trough?
-The scenario involves a trough that is 10 feet long and 6 feet across at the top, with water being pumped into it at a rate of 9 cubic feet per second. The goal is to find out how fast the water level is rising when the water is 2 feet deep.
How is the volume of the water in the trough related to its height?
-The volume of the water in the trough is related to its height by the formula V = (15/2) * H^2, where H is the height of the water and V is the volume.
What is the rate at which the water level is rising in the trough?
-The rate at which the water level is rising (dh/dt) is calculated to be 3/10 feet per second when the water is 2 feet deep.
Outlines
🎣 Calculating the Rate of Change of Angle in a Fishing Scenario
The first paragraph introduces a related rates problem involving a fish being reeled in under a bridge. The key objective is to find the rate at which the angle (θ) between the fishing line and the water surface is changing. Given the bridge is 16 feet above the water, and the fish is being reeled in at a rate of 2 feet per second, the problem uses trigonometric functions, specifically the tangent function, to establish a relationship between θ, the distance from the water (x), and the height of the bridge. The derivative of the tangent function is used to find dθ/dt, which is then solved for when x equals 20 feet, using basic trigonometric identities and algebraic manipulation to arrive at the final rate of change of the angle, which is 22.5 inches per second.
🚶♂️ Related Rates in a Shadow Length Problem
The second paragraph discusses a related rates problem concerning the shadow of a man walking away from a light pole. The scenario involves similar triangles to establish a relationship between the height of the light pole, the man's height, and the lengths of the shadows. The man's walking speed is given as 5 feet per second, and the problem involves finding the rate of change of the tip of the shadow (dx/dt) and the length of the shadow (d(X-Y)/dt). By setting up and solving the equations for the similar triangles, the rate of change of the tip of the shadow is found to be 8 feet per second, and the rate of change of the shadow's length is determined to be 3 feet per second.
💧 Rate of Water Level Rise in a Trough
The final paragraph presents a related rates problem involving the filling of a triangular trough with water. The goal is to determine how fast the water level is rising (dh/dt) when the water depth is 2 feet. The problem uses the volume formula for a triangular prism, which is the base times the height divided by 2, and multiplies by the length of the trough (10 feet). By expressing the base in terms of the height and taking the derivative with respect to time, the rate of change of the water level is calculated. Given the water is pumped in at a rate of 9 cubic feet per second, the final calculation shows that the water level is rising at a rate of 0.3 feet per second.
Mindmap
Keywords
💡Related Rates
💡Tangent Function
💡Derivative
💡Secant Function
💡Chain Rule
💡Pythagorean Theorem
💡Similar Triangles
💡Volume
💡Cone
💡Rate of Change
Highlights
Introduction to related rates problems involving a fish being reeled in and a bridge above water.
Setting up a geometric triangle to represent the angle between the fishing line and the water.
Using the tangent function to relate the angle theta to the bridge height and line length.
Differentiating the tangent function with respect to time to find the rate of change of the angle.
Solving for the rate of change of the angle (dθ/dt) when the line is 20 feet long.
Applying the Pythagorean theorem to find the length of the line when it is 20 feet.
Calculating the cosine squared of the angle to simplify the derivative for dθ/dt.
Final calculation of the rate of change of the angle as 2/25 feet per second.
Transition to a new example involving a person walking away from a light pole.
Using similar triangles to relate the height of the person and the light pole to the tip of the shadow.
Finding the rate of change of the tip of the shadow (dx/dt) as the person walks away.
Deriving the relationship between the person's walking speed and the shadow tip's rate of change.
Calculating the rate at which the shadow tip moves as 8 feet per second.
Exploring the rate of change of the shadow's length as the person moves away.
Deriving the formula for the volume of a triangular prism to relate it to the water level in a trough.
Finding the rate at which the water level rises in the trough as 3/10 feet per second.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: