Green's Theorem (Circulation & Flux Forms with Examples)
TLDRIn this educational video, Houston Mathprep explores Green's Theorem, a powerful tool for simplifying circulation and flux line integrals over closed curves. The script explains the theorem's two forms, circulation and flux, and demonstrates their application with examples, including calculating over a unit circle and a triangular region. It emphasizes the importance of understanding the vector field's properties, such as curl and divergence, and choosing the right integration bounds and methods. The video concludes with a teaser for further exploration of these concepts in upcoming content.
Takeaways
- 📘 Green's theorem is a mathematical tool used to simplify the calculation of circulation and flux line integrals over closed curves.
- 🔄 The circulation form of Green's theorem states that the line integral of a vector field over a closed curve is equal to the double integral of the difference between the partial derivatives of the vector field's components.
- 🔲 The double integral in Green's theorem is taken over the region enclosed by the closed curve, while the line integral is over the curve itself, showing a direct relationship between the two.
- 📐 For Green's theorem to apply, the partial derivatives of the vector field's components must exist over the region of interest.
- 🔍 The 2D curl of a vector field, represented by the difference of the partial derivatives, is crucial in the circulation form of Green's theorem.
- 🔍🔄 If the partial derivatives are equal, indicating a gradient field, the circulation integral will be zero, as the field is conservative.
- 📏 The choice of integration bounds and the order of integration (dydx, dxdy, or polar coordinates) depends on the shape of the region in the plane.
- 🌐 An example of applying Green's theorem is calculating the circulation of a vector field over the unit circle using polar coordinates.
- ⚫ The flux form of Green's theorem is used to calculate the integral of a vector field's normal component over a closed curve, which is related to the two-dimensional divergence of the field.
- 🔄🔄 In the flux form, the integral represents the amount of flow entering or leaving a region, and it is calculated as the sum of the partial derivatives of the vector field's components.
- 🌀 An example of a rotational field was given, where the flux through a unit circle was zero because the field had no divergence, indicating no net flow in or out.
Q & A
What is the main topic of the video?
-The main topic of the video is Green's Theorem and its application as a shortcut for calculating circulation and flux line integrals over closed curves.
What does the circulation form of Green's Theorem state?
-The circulation form of Green's Theorem states that the line integral of a vector field F over a closed curve C is equal to the double integral over the region inside C of the difference between the partial derivatives of the components of F.
What is the significance of the symbol 'round symbol' in the integral notation?
-The 'round symbol' in the integral notation signifies that the integration is being performed over a closed curve.
What is the difference between circulation and flux in the context of Green's Theorem?
-Circulation refers to the line integral of a vector field over a closed curve, representing the net circulation around the curve. Flux, on the other hand, refers to the component of the vector field that is perpendicular to the surface, indicating the flow through the surface.
What is the condition for Green's Theorem to be applicable to a line integral?
-Green's Theorem can be applied to a line integral when the curve C is a closed curve, such as a circle, square, triangle, or ellipse, and not just a path from one point to another.
What is the 2D curl of a vector field F?
-The 2D curl of a vector field F, given by the difference between the partial derivatives of its components (∂Nx - ∂My), represents the circulation density or the k-th component of curl in two dimensions.
Under what circumstances would the circulation integral be zero according to the video?
-The circulation integral would be zero when the partial derivatives ∂Nx and ∂My are the same, indicating that the field is a gradient field or a conservative field.
What are the different ways to calculate the differential area element 'da' in the double integral?
-The differential area element 'da' can be calculated in various ways depending on the shape of the region in the xy-plane, such as using dydx, dxdy, or in polar coordinates, rdrdθ.
Can you provide an example of calculating circulation using Green's Theorem from the video?
-An example from the video is calculating the circulation over the unit circle counterclockwise with the vector field (-3y, 3x). The process involves setting up a double integral using polar coordinates and evaluating it to get a result of 6π.
What is the difference between the circulation and flux forms of Green's Theorem?
-The circulation form of Green's Theorem deals with the line integral of the vector field F dot T (tangent) over a closed curve, while the flux form deals with the line integral of the vector field F dot N (normal) over a closed curve. The functions inside the double integral for each form are different, involving the sum of partial derivatives for flux and the difference for circulation.
How does the video explain the concept of divergence in the context of Green's Theorem?
-The video explains that the sum of the partial derivatives of the components of a vector field (∂Mx + ∂Ny) represents the two-dimensional divergence, which measures how much the vector field is spreading out at particular points and is used in the flux form of Green's Theorem.
Can you give an example of calculating flux using the flux form of Green's Theorem from the video?
-An example from the video is calculating the flux over the unit circle with the vector field (-3y, 3x). However, since the vector field is rotational with no flow in or out, the flux integral evaluates to zero.
What are the prerequisites for using Green's Theorem to evaluate a line integral?
-To use Green's Theorem, one must be evaluating a line integral over a closed curve, and it is necessary to be able to set up and evaluate the double integral easily. Additionally, one should be comfortable with identifying whether to use the circulation or flux form and knowing which partial derivatives to use in each case.
Outlines
📚 Introduction to Green's Theorem and Its Application
This paragraph introduces Green's Theorem, focusing on its use as a shortcut for calculating circulation and flux line integrals over closed curves. The circulation form of the theorem is presented, highlighting the equivalence between a line integral over a closed curve and a double integral over the enclosed region. Key concepts such as the 2D curl, conservative fields, and the conditions under which Green's Theorem can be applied are discussed. An example of calculating circulation over a unit circle using the theorem is provided, illustrating the process of converting a line integral into a double integral and evaluating it in polar coordinates.
📘 Green's Theorem for Circulation Over a Triangle
The second paragraph delves into applying Green's Theorem to calculate circulation over a triangular region with vertices at (0,0), (2,0), and (2,2) in the context of a vector field y, -x. The process involves setting up the double integral using the region's bounds and the partial derivatives of the field's components. The integration is performed using Cartesian coordinates, and the result is a circulation value of negative 4, indicating the net movement within the field over the triangular path.
📙 Exploring Flux Form of Green's Theorem and Divergence
This section introduces the flux form of Green's Theorem, which is used to calculate the flux integral over a closed curve by considering the normal component of the vector field. The concept of two-dimensional divergence is explained as a measure of how much a vector field spreads out. Examples are given, including calculating flux over the unit circle with a rotational field, resulting in zero flux due to the field's circular flow. Another example involves a triangular region with a field of 2x, y, leading to a flux calculation that yields a value of six.
📓 Summary of Green's Theorem and Preview of Upcoming Topics
The final paragraph summarizes the key points of Green's Theorem, emphasizing the importance of understanding whether to use the circulation or flux form and which partial derivatives to include in the function. It also previews upcoming content on vector fields, specifically the concepts of curl and divergence, and encourages viewers to watch the next video for further exploration of these topics.
Mindmap
Keywords
💡Green's Theorem
💡Circulation
💡Flux
💡Closed Curve
💡Vector Field
💡Partial Derivatives
💡2D Curl
💡Conservative Field
💡Polar Coordinates
💡Divergence
Highlights
Introduction to Green's Theorem and its application as a shortcut for circulation and flux line integrals over closed curves.
Explanation of the circulation form of Green's Theorem and its relation to line integrals over a closed curve.
The importance of the round symbol in the integral indicating integration over a closed curve.
The equivalence of the circulation integral and the double integral over the region inside the boundary.
Conditions for using Green's Theorem: existence of partial derivatives of M and N over the region.
The 2D curl of F and its significance in the circulation integral.
The concept of a gradient field and its relation to conservative fields where circulation is zero.
Differentiation between calculating the double integral using dA in Cartesian or polar coordinates based on the region's shape.
Example calculation of circulation over the unit circle using a vector field with components -3y and 3x.
Use of polar coordinates for the unit circle example and simplification of the integral.
Result of the circulation integral over the unit circle yielding a value of 6π.
Introduction of the flux form of Green's Theorem and its application to line integrals in terms of flux.
Explanation of the two-dimensional divergence and its role in the flux integral.
Example of flux calculation over the unit circle with a rotational vector field resulting in zero flux.
Application of Green's Theorem to a triangular region with a vector field of y and -x.
Calculation of flux over the triangular region resulting in a value of six.
General guidelines for using Green's Theorem, emphasizing the need for a closed curve and the ability to evaluate the double integral.
Upcoming video teaser on the concepts of curl and divergence in more depth.
Transcripts
Browse More Related Video

Lec 24: Simply connected regions; review | MIT 18.02 Multivariable Calculus, Fall 2007

Green's Theorem, explained visually
Stokes' Theorem // Geometric Intuition & Statement // Vector Calculus

Divergence theorem example 1 | Divergence theorem | Multivariable Calculus | Khan Academy
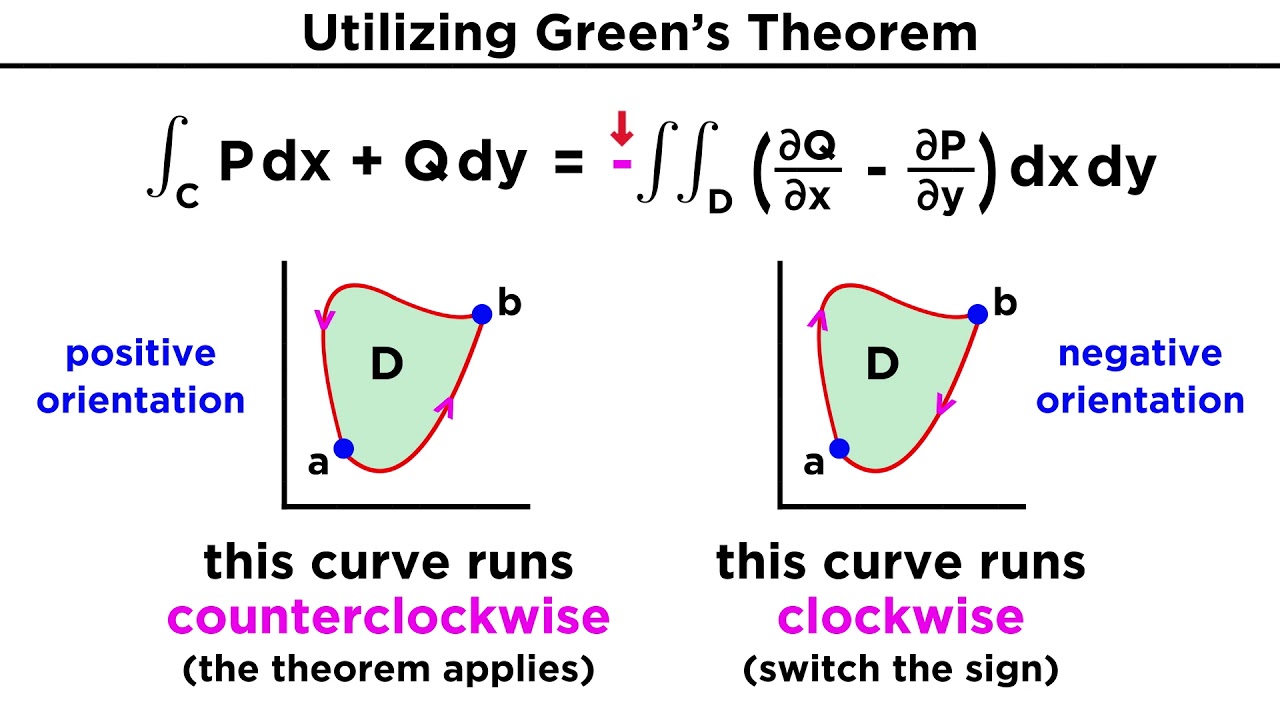
Green's Theorem

Lec 23: Flux; normal form of Green's theorem | MIT 18.02 Multivariable Calculus, Fall 2007
5.0 / 5 (0 votes)
Thanks for rating: