What is Central Tendency – An Introduction to Mean, Median, and Mode in Statistics (5-1)

Research By Design
18 Aug 201604:25
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Dr. Todd Daniel introduces viewers to the concept of displaying data numerically, focusing on the importance of central tendency. He explains the three measures of central tendency—mean, median, and mode—and their applications. The video clarifies when to use each measure, considering the scale of measurement and the distribution's shape. It emphasizes the benefits of simplification and prediction that these measures provide, using relatable examples to illustrate their practical significance.

Takeaways
  • 📊 The video discusses three measures of central tendency: mean, median, and mode, and their applications in data analysis.
  • 🔍 Central tendency is used to find the center of a data set and is crucial for understanding data distribution.
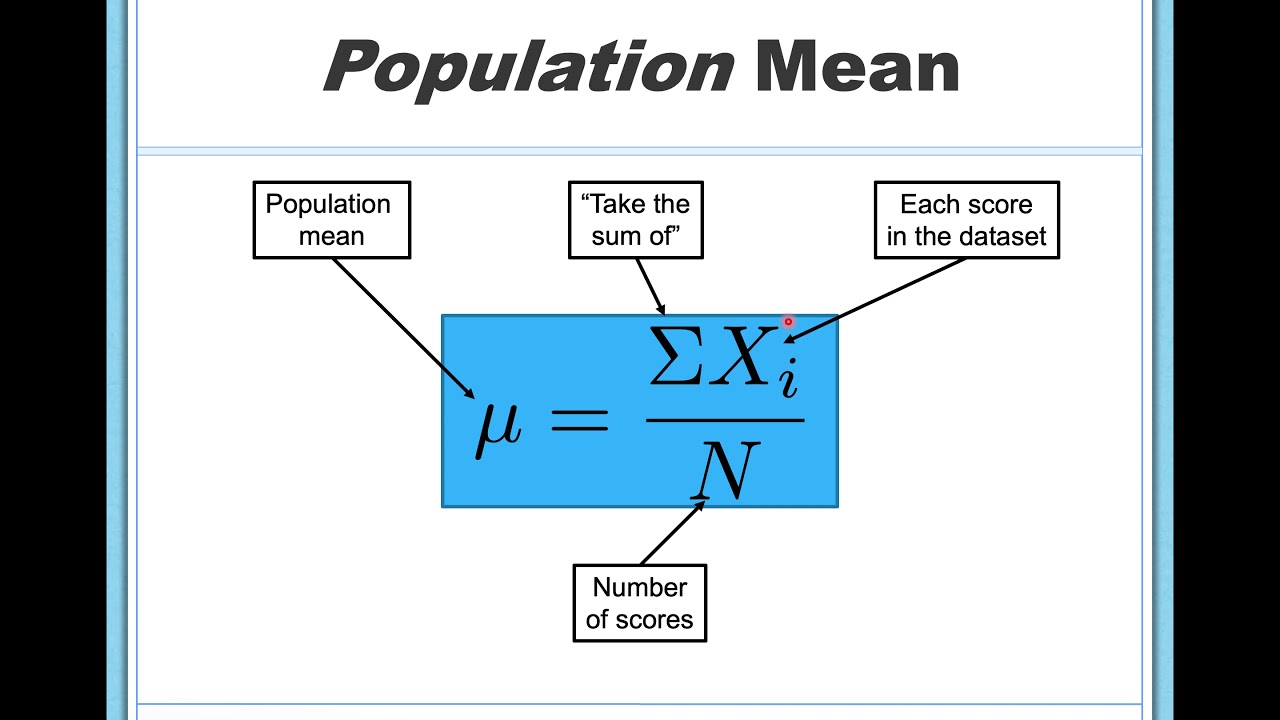
  • 🧠 The mean is the average of the data and is typically used with interval or ratio level data.
  • 📈 The median is the middle value in a data set and is less affected by outliers, making it useful for skewed distributions.
  • 📚 The mode is the most frequently occurring value in the data and is applicable to nominal and ordinal data.
  • 🤔 Two key questions addressed are: what single number best represents the data, and how spread out or clustered the scores are.
  • 🏀 An example is given using basketball players and horse jockeys to illustrate the concept of central tendency in everyday assumptions.
  • 📊 Simplification is a benefit of central tendency as it reduces complex data into a single representative number.
  • 🔮 Central tendency aids in prediction, such as estimating future needs based on average family size and population growth.
  • ⚖️ The choice of central tendency measure depends on the scale of measurement and the shape of the data distribution.
  • 📉 The mean, median, and mode each have specific uses and are chosen based on the characteristics of the data set being analyzed.
  • 📝 Understanding central tendency helps in interpreting data and making informed decisions based on statistical analysis.
Q & A

  • What is the main focus of the video script provided by Dr. Todd Daniel?

    -The main focus of the video script is to teach how to display data with numbers, specifically how to determine and understand measures of central tendency such as mean, median, and mode.

  • Why is it important to know the center of the data?

    -Knowing the center of the data is important because it helps to answer questions about where the middle of the distribution is and provides a single number that can represent the entire data set, which is useful for simplification and prediction.

  • What are the three measures of central tendency mentioned in the script?

    -The three measures of central tendency mentioned are mean, median, and mode.

  • What does the mean represent in terms of data?

    -The mean represents the average value of the data set, which is calculated by summing all the data points and dividing by the number of points.

  • How is the median different from the mean?

    -The median is the middle value of a data set when the numbers are arranged in numerical order, whereas the mean is the average value. The median is less affected by extreme values and provides a better representation of the center for skewed data.

  • What is the mode and when is it most useful?

    -The mode is the value that appears most frequently in a data set. It is most useful when dealing with categorical data or when the data set contains non-numeric values.

  • Why might the mean not be the best measure of central tendency for a skewed distribution?

    -The mean might not be the best measure for a skewed distribution because it can be heavily influenced by outliers or extreme values, which can distort the central location of the data.

  • What is the benefit of using measures of central tendency for simplification?

    -The benefit of using measures of central tendency for simplification is that it reduces the complexity of the entire data set to a single number, making it easier to understand and communicate the general trend or location of the data.

  • How can measures of central tendency be used for prediction?

    -Measures of central tendency can be used for prediction by providing an estimate or average that can help forecast future trends or needs, such as predicting the number of new classroom seats needed based on the average family size.

  • What factors determine which measure of central tendency to use?

    -The choice of a measure of central tendency depends on the scale of measurement (nominal, ordinal, interval, or ratio) and the shape of the data distribution, especially if it is skewed or kurtotic.

  • Can you provide an example of how measures of central tendency are used in everyday life?

    -An example from the script is the assumption about the height of a basketball player or a horse jockey based on the general height tendencies of those professions, which is an informal use of measures of central tendency.

Outlines
00:00
📊 Introduction to Central Tendency

Dr. Todd Daniel introduces the concept of displaying data with numbers, focusing on the importance of understanding central tendency. He explains that central tendency is a measure that indicates the center of a data set and is crucial for understanding whether the data is generally high or low. The video will cover three specific measures of central tendency: mean, median, and mode, and when to use each. Dr. Daniel also emphasizes the benefits of central tendency, such as simplification of raw data and the ability to predict or estimate future needs based on the average or common values.

Mindmap
Keywords
💡Central Tendency
Central tendency refers to a single value that represents a set of data by identifying the center of the data. In the video, central tendency is the primary focus, as it discusses how to determine the middle or average point of a data set. The script mentions three measures of central tendency and explains their importance in understanding and summarizing data.
💡Mean
Mean, also known as the average, is calculated by summing all the values in a data set and then dividing by the number of values. It is one of the measures of central tendency discussed in the video. The mean is particularly useful for interval or ratio level data and is used to find the arithmetic center of the data, as illustrated by the example of a test score and the class average.
💡Median
Median is the middle value of a data set when the numbers are arranged in ascending or descending order. It is another measure of central tendency and is mentioned in the video as a way to find the center of the data. The median is less affected by extreme values and is often used when the data distribution is skewed.
💡Mode
Mode is the value that appears most frequently in a data set. It is the third measure of central tendency discussed in the video. The mode provides insight into the most common value or category within the data, which can be particularly useful for nominal or ordinal data types.
💡Data Distribution
Data distribution refers to the way data points are spread out in a set. The video script discusses the importance of understanding the distribution's shape, such as whether it is skewed or kurtotic, when choosing a measure of central tendency. The shape of the distribution can affect which measure best represents the center of the data.
💡Skewness
Skewness is a measure that indicates the asymmetry of the data distribution. In the video, skewness is mentioned as a factor that can influence the choice of central tendency. A highly skewed distribution may not be well represented by the mean, leading to the consideration of the median or mode.
💡Kurtosis
Kurtosis is a measure that describes the 'tailedness' of the probability distribution. The video briefly touches on kurtosis as another factor affecting the selection of a central tendency measure. A distribution with high kurtosis has more extreme values and may require a specific measure of central tendency to accurately represent the data.
💡Scale of Measurement
The scale of measurement categorizes data into types such as nominal, ordinal, interval, or ratio. The video script explains that the choice of central tendency measure depends on the scale of the data. For instance, the mean is typically used with interval or ratio data, which have specific numerical values.
💡Simplification
Simplification in the context of the video refers to the process of reducing complex data sets to a single, easily understood number using a measure of central tendency. This concept is highlighted as a benefit, allowing for easier interpretation and communication of data.
💡Prediction
Prediction, as discussed in the video, is the use of a measure of central tendency to estimate future outcomes or needs. The script provides an example of using the average number of children per family to predict the number of new classroom seats needed, demonstrating how central tendency aids in forecasting.
💡Basketball Player
The term 'basketball player' is used in the video as an example to illustrate how assumptions about central tendency can be made based on general knowledge about a group. It suggests that basketball players are generally tall, indicating a high average height, which is a measure of central tendency.
💡Horse Jockey
The term 'horse jockey' is used as another example in the video to show how central tendency can influence assumptions. It is suggested that jockeys are generally short, indicating a low average height, which again relates to the concept of central tendency.
Highlights

Introduction to displaying data with numbers, in addition to pictures.

Central tendency is the key to understanding where the center of the data lies.

Three main measures of central tendency: mean, median, and mode.

Explanation of when to use each measure of central tendency.

Central tendency answers the question of how representative a single number is for the entire data set.

Understanding if scores are generally high or low using measures of central tendency.

The importance of context in interpreting raw scores, exemplified by test scores and class averages.

Using central tendency to make assumptions about groups, like basketball players' heights.

Benefits of simplification provided by measures of central tendency for complex data sets.

The predictive power of central tendency for estimating future needs or scores.

The average family having 2.3 children as an example of predictive use of central tendency.

Determining the appropriate measure of central tendency based on the scale of measurement.

The influence of data distribution shape on the choice of central tendency measure.

Mean is typically used with interval or ratio level data for central tendency.

The handling of skewed or kurtotic distributions when choosing a central tendency measure.

The uniqueness of each measure of central tendency in describing data distribution.

Transcripts

Browse More Related Video

Mean, Median, Mode, and Outliers: Measures of Central Tendency

Measures of Central Tendency (Mean, Median, Mode)

Understanding Central Tendency

Statistics: The average | Descriptive statistics | Probability and Statistics | Khan Academy

What is Variability? – An Introduction to Variance in Statistics (6-1)

What are Mean, Median and Mode? | Statistics | Infinity Learn

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsData AnalysisCentral TendencyMeanMedianModeFlipped ClassroomData DisplayEducationalPredictive AnalyticsMeasures of Tendency