How To Find The Greatest Common Factor Quickly!

The Organic Chemistry Tutor
17 Jul 201710:28
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script teaches the method of finding the Greatest Common Factor (GCF) of given numbers. It illustrates the process by breaking down numbers into their prime factors and identifying the common ones. Examples include finding the GCF for pairs and groups of numbers, as well as for monomials involving variables. The script emphasizes that the GCF is the highest common prime factor shared among the numbers, and guides viewers through various examples to solidify the concept.

Takeaways
  • πŸ”’ The method to find the greatest common factor (GCF) is by prime factorization of the given numbers.
  • πŸ“ The prime factorization of 15 is 3 * 5, and for 35 it is 7 * 5, with 5 being the GCF.
  • πŸ“š To find the GCF of 21 and 28, prime factorization reveals 7 as the common factor, thus the GCF.
  • πŸ“ For 22 and 55, prime factorization shows 11 as the GCF, since it's the only common factor.
  • πŸ“‰ The GCF of 12 and 16 is 4, as both numbers have two 2s in their prime factorization.
  • πŸ“ˆ The GCF of 15 and 18 is 3, as it's the only prime number common to both.
  • πŸ“Š For 24 and 40, the GCF is 8, since both numbers have three 2s in their prime factorization.
  • πŸ“Œ When finding the GCF of monomials, such as 6X and 9x^2, the process involves identifying common prime factors and variables, resulting in 3X as the GCF.
  • πŸ“œ For monomials with variables and exponents, like 12xy and 15x^2y^3, the GCF is determined by common prime factors and the lowest power of variables, which is 3xy.
  • πŸ“‹ The GCF between 24x^2y^3 and 30x^4y^4 involves identifying the common prime factors and the lowest powers of variables, resulting in 6x^2y^3.
  • πŸ“ For three numbers, like 12, 18, and 20, the GCF is found by identifying the common prime factors in all numbers, which is 2 in this case.
  • πŸ“‰ To find the GCF of 30, 48, and 56, the common prime factor among all is 2, making it the GCF.
Q & A

  • What is the greatest common factor (GCF) of 15 and 35?

    -The GCF of 15 and 35 is 5, as both numbers have 5 as a common prime factor.

  • How do you find the prime factorization of a composite number?

    -You break down the composite number into a product of prime numbers. For example, 35 is broken down into 7 * 5.

  • What is the GCF of 21 and 28?

    -The GCF of 21 and 28 is 7, as it is the highest prime number found in the prime factorization of both numbers.

  • What is the prime factorization of 22?

    -The prime factorization of 22 is 2 * 11.

  • How many common prime factors are needed to determine the GCF of two numbers?

    -You only need to identify the highest common prime factor present in both numbers' prime factorizations to determine the GCF.

  • What is the GCF between 12 and 16?

    -The GCF of 12 and 16 is 4, as both numbers have two 2's in their prime factorizations.

  • Can the GCF be a variable when dealing with monomials?

    -Yes, the GCF can include variables when dealing with monomials, such as 3x in the case of 6X and 9x^2.

  • What is the GCF of 24 and 40?

    -The GCF of 24 and 40 is 8, as both numbers have three 2's in their prime factorizations.

  • How do you find the GCF of three numbers?

    -You find the prime factorization of each number and then identify the common prime factors present in all three, with the smallest power of each common factor determining the GCF.

  • What is the GCF between 30, 48, and 56?

    -The GCF of 30, 48, and 56 is 2, as it is the only prime factor common to all three numbers.

  • How does the process of finding the GCF differ when there are variables involved?

    -The process is similar; you identify the common variables and their highest powers that are present in both expressions to determine the GCF.

Outlines
00:00
πŸ”’ Finding the Greatest Common Factor (GCF) Through Prime Factorization

This paragraph introduces the concept of finding the greatest common factor (GCF) between two numbers by using prime factorization. It demonstrates the process with examples, such as determining the GCF of 15 and 35, which is 5, and 21 and 28, which is 7, by breaking down each number into its prime factors and identifying the highest common factor. The method is further applied to additional pairs of numbers, emphasizing the importance of recognizing common prime factors to find the GCF.

05:03
πŸ“š Applying Prime Factorization to Monomials and Multiple Numbers

The second paragraph extends the GCF concept to monomials, which may include variables, and to sets of three numbers. It illustrates how to find the GCF for expressions like 6X and 9x^2, identifying 3X as the GCF. The process is also shown for 12xy and 15x^2y^3, where the GCF is 3xy. The paragraph further explains how to find the GCF for three numbers, such as 12, 18, and 20, and for 30, 48, and 56, concluding that the GCF in both cases is 2, due to the presence of the number 2 in the prime factorization of all given numbers.

10:03
πŸ“‰ Recapitulation of the GCF Concept

The final paragraph serves as a brief recapitulation of the GCF concept, reiterating the importance of identifying the greatest common factor among numbers. It does not provide new examples or methods but reinforces the idea that the GCF is the highest number that divides all given numbers without a remainder, and it is determined by examining their prime factorizations.

Mindmap
Keywords
πŸ’‘Greatest Common Factor (GCF)
The Greatest Common Factor, also known as the greatest common divisor, is the largest positive integer that divides two or more numbers without a remainder. In the video, the GCF is the central concept, as it is used to determine the common prime factors between pairs or groups of numbers. For example, the GCF of 15 and 35 is 5, as it is the highest number that divides both without leaving a remainder.
πŸ’‘Prime Factorization
Prime factorization is the process of breaking down a composite number into the product of its prime factors. This concept is fundamental in the video, as it is the method used to find the GCF. The script demonstrates prime factorization with numbers like 15, which factors into 3 * 5, and 35, which factors into 7 * 5.
πŸ’‘Composite Number
A composite number is a positive integer greater than 1 that has factors other than 1 and itself. In the context of the video, composite numbers are broken down into their prime factors to find commonalities and determine the GCF. For instance, 35 is a composite number that factors into 7 * 5.
πŸ’‘Common Factor
A common factor is a number that divides two or more numbers. Within the video's narrative, identifying common factors is crucial for determining the GCF. The script shows this by comparing the prime factors of different numbers, such as 21 and 28, to find that 7 is a common factor.
πŸ’‘Divisibility
Divisibility refers to the property of a number being able to be divided by another number without leaving a remainder. The concept is used in the video to explain that the GCF must be a number that each number in the set can be divided by evenly. For example, 40 and 24 are both divisible by 8, making 8 their GCF.
πŸ’‘Monomials
Monomials are algebraic expressions with only one term, which can be a variable, a constant, or a product of variables and constants. In the video, the GCF is extended to monomials, such as finding the GCF of 6X and 9X^2, which involves looking at the coefficients and variables to determine the common factors.
πŸ’‘Variables
Variables are symbols, usually letters, that represent unknown quantities in algebraic expressions. The video discusses how to find the GCF when variables are involved, such as in the monomials 12xy and 15x^2y^3, where the GCF is determined by considering both the numerical coefficients and the variables present.
πŸ’‘Coefficients
Coefficients are the numerical factors that multiply variables in algebraic terms. In the context of the video, when finding the GCF of monomials, coefficients are considered to identify common numerical factors. For example, in the monomials 6X and 9X^2, the coefficient 3 is common to both.
πŸ’‘Prime Numbers
Prime numbers are natural numbers greater than 1 that have no positive divisors other than 1 and themselves. The video emphasizes prime numbers as the building blocks for finding the GCF through prime factorization. Every composite number in the script is broken down into prime numbers to identify common factors.
πŸ’‘Multiple Meanings
In the video, certain terms like 'factor' can have multiple meanings, such as a number that divides another or the numerical part of a term in algebra. The script uses 'factor' in both contexts, demonstrating how to find common factors between numbers and how to include factors in the GCF of monomials.
Highlights

Introduction to finding the greatest common factor (GCF) between two numbers.

Method of finding GCF through prime factorization exemplified with numbers 15 and 35.

Explanation of prime factorization of 15 and 35, identifying 5 as the GCF.

Demonstration of finding GCF for 21 and 28, identifying 7 as the common factor.

Prime factorization of 22 and 55, with 11 as the GCF.

Instructions to find GCF between 12 and 16, with a pause for audience participation.

Prime factorization of 12 and 16, concluding with 4 as the GCF.

Finding the GCF between 15 and 18, identifying 3 as the greatest common factor.

Prime factorization of 24 and 40, with 8 as the GCF.

Guidance on finding GCF between monomials, such as 6X and 9x^2, with 3X as the result.

Process of finding GCF between 12xy and 15x^2y^3, identifying 3xy as the common factor.

Finding GCF between 24x^2y^3 and 30x^4y^4, with 6x^2y^3 as the result.

Introduction to finding GCF between three numbers: 12, 18, and 20, with 2 as the GCF.

Prime factorization of 30, 48, and 56, identifying 2 as the common GCF.

Emphasis on the importance of identifying common prime factors in both numbers to find the GCF.

Practical application of the method in various examples to solidify understanding.

Transcripts

Browse More Related Video

Greatest Common Factor (GCF)

How To Find The LCM and HCF Quickly!

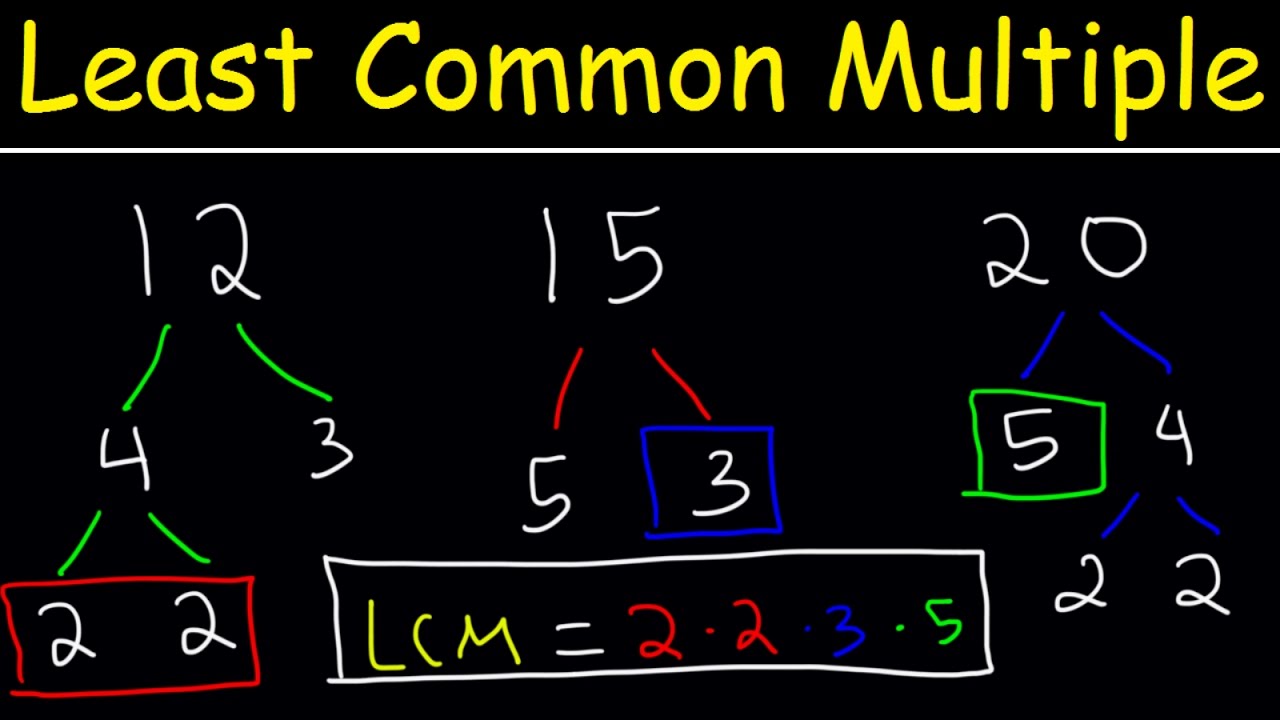
How To Find The LCM of 3 Numbers - Plenty of Examples!

Factoring Polynomials - By GCF, AC Method, Grouping, Substitution, Sum & Difference of Cubes

GED MATH 2024 Preparation Course - from the Absolute Beginning to Advanced Level

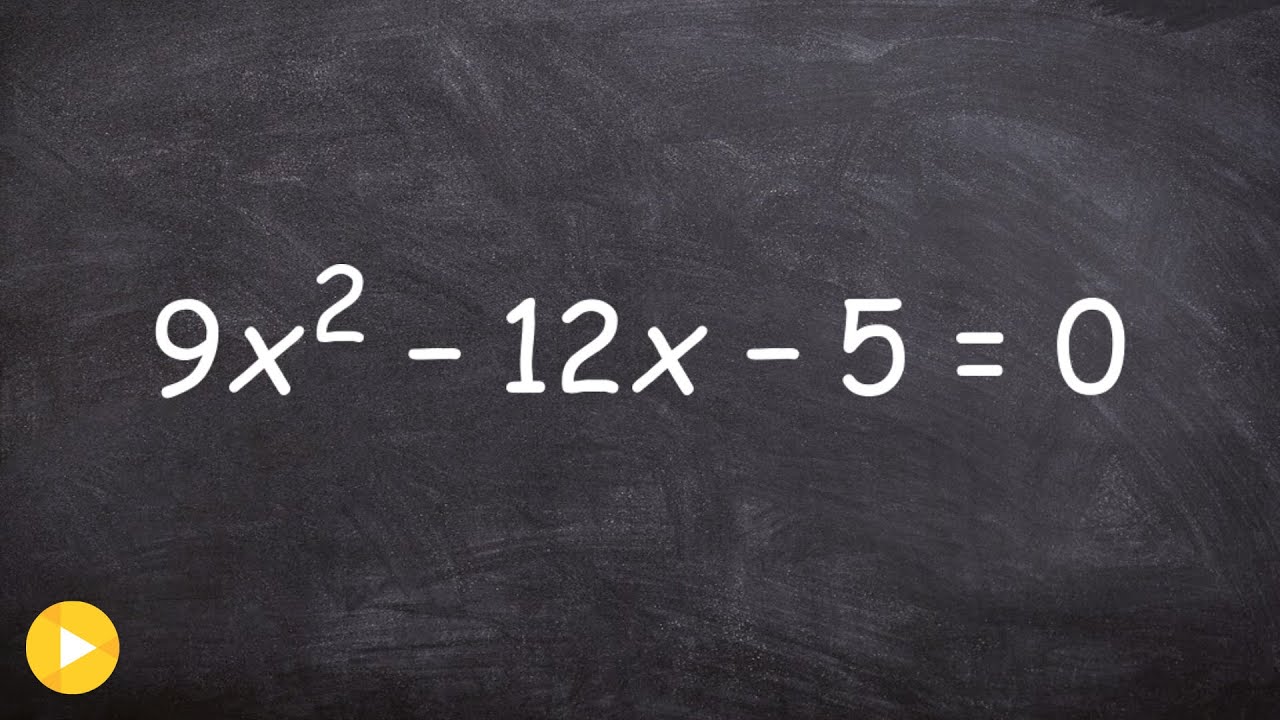
Learn the ac method for factoring and solving a quadratic equation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Greatest Common FactorPrime FactorizationMathematics LessonEducational ContentNumber TheoryFactor AnalysisGCF MethodMath PracticeAlgebra BasicsLearning Resource