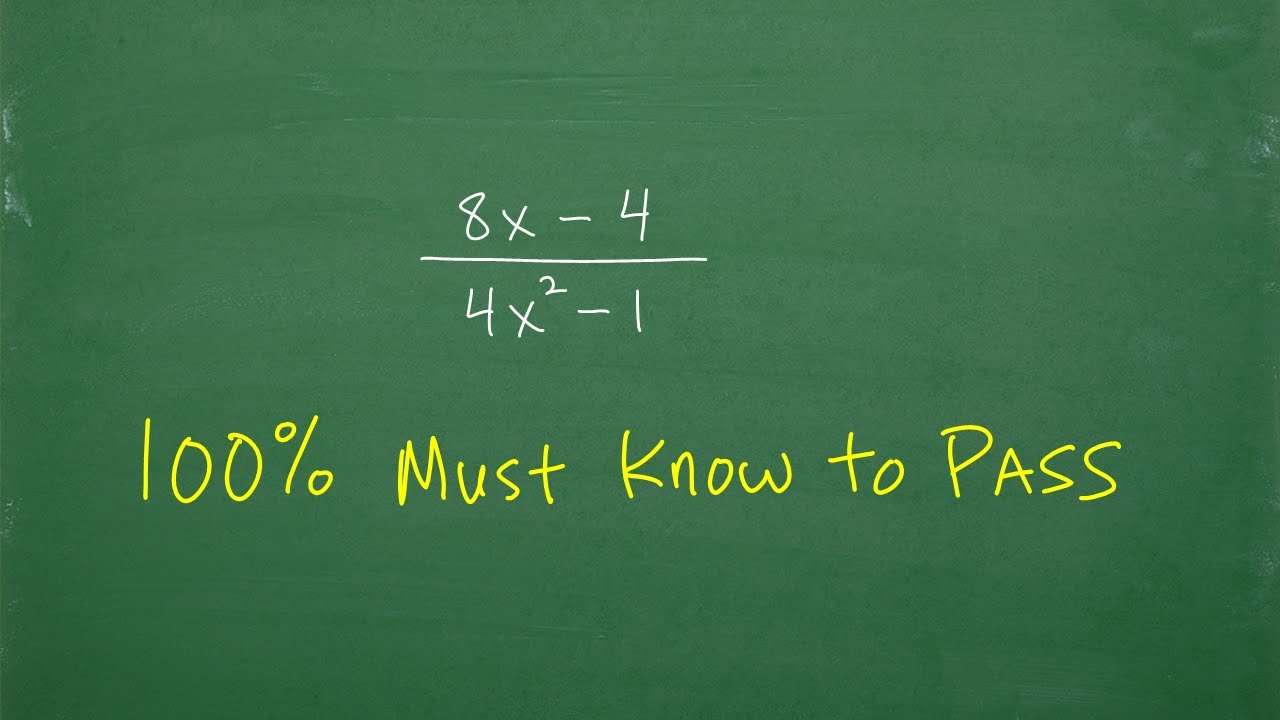Best FACTORING Hack EVER! - Part 2
TLDRThis video script offers an in-depth guide on factoring trinomials with leading coefficients other than one, building on the techniques introduced in 'Factoring Hack Part One.' The presenter, John, founder of Taba Class Math, explains the methodical approach to factoring, starting with identifying the greatest common factor and using it to split the middle term. He illustrates the process with examples, emphasizing the importance of practice for mastering algebra. The script also promotes John's comprehensive math courses and resources for various exams and learning levels.
Takeaways
- 📚 The video focuses on teaching how to factor trinomials, especially when the leading coefficient is not one, which is a continuation from 'best factoring hack part one'.
- 🔗 There's a link to part one of the video and an algebra playlist for further learning, suggesting a series of related content.
- 👨🏫 The presenter, John, is the founder of Taba Class Math and a middle and high school math teacher, emphasizing his credibility and experience in teaching.
- 🎓 John offers over 100 online math courses covering a wide range of topics, including test preparation for various exams like GED, SAT, and more.
- 📘 He emphasizes the importance of taking good math notes as a key to success in mathematics, and offers comprehensive math notes for different levels.
- 📝 The script provides a step-by-step method for factoring trinomials with a leading coefficient other than one, starting with identifying the greatest common factor (GCF).
- 🔢 It illustrates the process with an example, showing how to break down the middle term of the trinomial into two parts whose factors sum up to the middle coefficient.
- 🔄 The technique involves grouping and factoring out the GCF from each group, which should yield the same factor if done correctly.
- 📉 The video acknowledges that factoring is a foundational skill in algebra and is critical for success in the subject.
- 📈 Practice problems are provided to help viewers apply the taught technique, emphasizing the importance of practice in mastering factoring.
- 👍 The video concludes with encouragement to like, subscribe, and follow the links in the description for more resources, highlighting the presenter's commitment to providing educational content.
Q & A
What is the main topic of the video?
-The main topic of the video is how to factor a trinomial with a leading coefficient that is not one, which is part of a series on factoring techniques.
What is the significance of the leading coefficient in factoring a trinomial?
-The leading coefficient is significant because it affects the method used for factoring. The video discusses techniques for trinomials with leading coefficients other than one, building on methods for when the leading coefficient is one.
What is the first step in factoring a trinomial with a non-one leading coefficient?
-The first step is to ensure the trinomial is in standard form, with the highest to lowest power of the variable, and then multiply the leading coefficient by the constant term to find a product that will be factored.
Why is it important to list the factors of the product obtained from the leading coefficient and constant term?
-Listing the factors is important to find a pair of factors that add up to the middle coefficient of the trinomial, which will be used to rewrite the middle term and proceed with the factoring process.
What does the video suggest if no pair of factors adds up to the middle coefficient?
-If no pair of factors adds up to the middle coefficient, the video suggests that the trinomial is prime and cannot be factored using the standard techniques.
What is the purpose of rewriting the middle term of the trinomial using the factors found?
-Rewriting the middle term allows for the application of group factoring, where common factors can be factored out from each group, leading to the complete factorization of the trinomial.
What is group factoring and how is it used in the factoring process?
-Group factoring is a technique where terms in an expression are grouped, and the greatest common factor (GCF) is factored out from each group, simplifying the expression towards its factored form.
How does the video emphasize the importance of note-taking in learning mathematics?
-The video emphasizes that students who take excellent math notes almost always have great math grades, suggesting that note-taking is a key component of understanding and retaining mathematical concepts.
What resources does the video creator offer for students studying for various math exams?
-The video creator offers over 100 different math courses, including test preparation for exams like the GED, SAT, ACT, teacher's certification exams, and more, which can be found on his website.
What advice does the video give for students who are struggling with factoring or other algebraic concepts?
-The video advises students to practice the techniques presented, review other relevant videos or courses, and to focus on understanding and applying the greatest common factor, special factoring rules, and the procedures for factoring trinomials.
Outlines
📚 Introduction to Factoring Trinomials and Algebra Techniques
This paragraph introduces the topic of the video, which is factoring trinomials with a leading coefficient other than one. It references a previous video (Part 1) that focused on trinomials with a leading coefficient of one. The speaker, John, founder of Taba Class Math and a middle/high school math teacher, emphasizes the importance of mastering factoring for success in algebra. He mentions his online math help program, which includes over 100 courses and test preparation for various exams. John also stresses the importance of note-taking for learning and offers comprehensive math notes for different levels. The paragraph concludes with a brief overview of factoring techniques, including using the greatest common factor (GCF) and special factoring rules like the difference of two squares.
🔍 Advanced Factoring Techniques for Non-Unity Leading Coefficients
The second paragraph delves into the specifics of factoring trinomials where the leading coefficient is not one. John explains that the technique used in the first part of the video series can be extended to handle these cases. He provides an example of factoring a trinomial with a leading coefficient of three and a constant term of eight, resulting in the product of 24. The process involves listing the factors of 24, looking for a pair that sums up to the middle term's coefficient (10 in this case), and then rewriting the trinomial using these factors. The goal is to find a pair of factors of the constant term that add up to the linear coefficient, which in this example is achieved with the factors 4 and 6.
📝 Step-by-Step Guide to Factoring Trinomials with Multiple Leading Coefficients
This paragraph continues the detailed explanation of factoring trinomials, focusing on the step-by-step process after identifying the correct pair of factors. It describes how to rewrite the middle term using the identified factors and then proceed with group factoring. John illustrates this with the example of factoring 3y^2 + 10y + 8, showing how to break down 10y into 4y + 6y, and then factor out the greatest common factor (GCF) from each group. The process results in the factored form of (3y + 4)(y + 2). The paragraph emphasizes the importance of practice and provides reassurance that the technique will become easier over time.
🧩 Applying Factoring Techniques to Practice Problems
The fourth paragraph presents two practice problems to apply the factoring techniques discussed earlier. John works through the problems, demonstrating how to find the correct factors of the constant term that sum up to the linear coefficient. The first problem involves factoring a trinomial with a leading coefficient of two and a constant term of ten, leading to the factored form of (2x + 5)(x + 2). The second problem involves a trinomial with a leading coefficient of three and a constant term of four, resulting in the factored form of (3a + 1)(a + 4). The paragraph encourages viewers to practice these techniques to improve their factoring skills.
🎓 Wrapping Up Factoring Techniques and Encouraging Further Learning
In the concluding paragraph, John summarizes the importance of the factoring techniques covered in the video and encourages viewers to continue learning and practicing these skills. He reminds viewers of the significance of factoring in algebra and suggests revisiting the part 1 video for additional context. John also promotes his algebra course for a more comprehensive understanding of factoring. He ends the video by inviting viewers to like, subscribe, and follow the links in the description for more resources, emphasizing his decades of experience in teaching mathematics and his confidence in the effectiveness of the techniques presented.
Mindmap
Keywords
💡Factoring
💡Trinomial
💡Leading Coefficient
💡Greatest Common Factor (GCF)
💡Special Factoring Rules
💡Group Factoring
💡Algebra
💡Test Preparation
💡Note-Taking
💡Online Math Help Programs
💡Factor Pairs
Highlights
Introduction to factoring trinomials with a leading coefficient other than one.
Link to Part One of the factoring hack video series.
Importance of mastering factoring for success in algebra.
Introduction of John, founder of Taba Class Math and a middle/high school math teacher.
Overview of John's online math help program and course offerings.
Emphasis on the significance of note-taking for math success.
Discussion on the distraction caused by smartphones in learning environments.
Explanation of the general approach to factoring using the greatest common factor (GCF).
Introduction of special factoring rules like the difference of two squares.
Differentiation between two types of trinomials in factoring.
Technique for factoring trinomials with a leading coefficient other than one.
Process of finding factors of the constant term and their sums to match the middle term.
Method of rewriting the middle term using the identified factors.
Group factoring technique to simplify the expression.
Final step of factoring out the common terms to reach the solution.
Practice problems to apply the learned factoring technique.
Emphasis on the importance of practice in mastering the factoring technique.
Conclusion and encouragement for viewers to apply the techniques in their math studies.
Invitation to subscribe to John's YouTube channel for more math resources.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: