AP Calculus Practice Exam Part 9 (FR #5)

Hittin' the Board with Mr. Vranderic

24 Apr 202322:51

EducationalLearning

32 Likes 10 Comments

TLDRThe script details a teacher's innovative approach to teaching, where students are required to watch educational videos at home and then practice in class. The teacher emphasizes the importance of being present and engaged. The lesson then shifts to a calculus problem involving the velocity and position functions of two friends, Brandon and Chloe, on a bike ride. The teacher guides students through finding antiderivatives, applying the mean value theorem, and using the intermediate value theorem to solve related problems, all while sharing personal anecdotes and encouraging students to review concepts.

Takeaways

📚 The teacher is implementing a new approach to the first unit by having students watch videos at home and then practice in class.
📱 The students are instructed to put their cell phones away before starting class to ensure focus and engagement.
🚴‍♂️ The script mentions friends Brandon and Chloe who are on a long bike ride, which is used as a context for discussing mathematical concepts.
📈 The discussion involves differentiable functions and the concept of velocity, with an emphasis on understanding the relationship between position, velocity, and acceleration in physics.
🔍 For Chloe's bike ride, the teacher calculates the position function by finding the antiderivative of her velocity function within a specific time frame.
🧮 The teacher demonstrates the process of taking derivatives and integrals, including handling natural exponential functions and their properties.
🏞️ An estimation of the distance Chloe travels is provided by evaluating the antiderivative at specific points and using the approximation of e to the power of a number.
🛣️ The teacher explains how to determine if a cyclist is increasing or decreasing speed by comparing the signs of velocity and acceleration.
📉 The concept of the mean value theorem is introduced to justify that there must be a time when Brandon's acceleration equals a given value during his bike ride.
🔄 The intermediate value theorem is used to argue that there must be a time when Brandon's and Chloe's velocities are equal during their respective rides.
🎓 The teacher encourages students to review the mean value theorem and the intermediate value theorem in preparation for an upcoming AP exam.

Q & A

What is the current activity the Juniors are engaged in according to the transcript?
-The Juniors are working on the first unit that was done in August. They are watching videos at home and then practicing in class.
What does the instructor emphasize about cell phones in the classroom?
-The instructor emphasizes that students should put their cell phones away before starting the class to ensure they are focused and awake.
What is the subject of the discussion involving Brandon and Chloe's bike ride?
-The subject is about calculating the distance traveled and the velocities of Brandon and Chloe during their bike ride using mathematical functions and calculus.
Why is the instructor making sure to specify the time frame for Chloe's bike ride when calculating her distance?
-The instructor specifies the time frame because the velocity function is piecewise, and the correct piece must be chosen to accurately calculate the distance traveled within that time frame.
What mathematical concept is used to find out how many miles Chloe has traveled halfway through her bike ride?
-The mathematical concept used is the antiderivative, which is applied to Chloe's velocity function to find her position function.
What function is Chloe's velocity function, and why is it significant in this context?
-Chloe's velocity function is a piecewise function. It is significant because it allows for different rates of speed at different times during her bike ride, which is essential for calculating the distance traveled.
What is the e term in the antiderivative calculation, and what does it represent?
-The e term represents the base of the natural logarithm, approximately equal to 2.7183. In the context of the antiderivative calculation, it is used to account for the exponential part of the velocity function.
How does the instructor determine the distance Chloe has traveled at the halfway point of her bike ride?
-The instructor evaluates the antiderivative at the time points 2 and 0, and then calculates the difference to find the distance traveled at the halfway point.
What is the significance of the mean value theorem in the context of Brandon's acceleration?
-The mean value theorem is used to justify that there exists a time at which Brandon's acceleration equals the given value of 2.5 miles per hour squared, based on the average rate of change of his velocity function.
What theorem is used to determine if there is a time when Brandon's and Chloe's velocities are equal, and why?
-The intermediate value theorem is used to determine if there is a time when the velocities are equal. It is used because both velocity functions are continuous, and the theorem states that if a continuous function changes sign over an interval, there must be a point where the function is zero.
How does the instructor use the concept of velocity and acceleration to explain Chloe's speed at three hours into her bike ride?
-The instructor calculates Chloe's velocity and acceleration at three hours using the appropriate piece of her velocity function. Since both velocity and acceleration are negative, they indicate that Chloe's speed is increasing.

Outlines

00:00

📚 Classroom Teaching and Bike Ride Analysis

The speaker discusses their teaching approach, where they have students watch instructional videos at home and then practice in class, emphasizing the importance of being present and engaged. They also delve into a mathematical problem involving Brandon and Chloe's bike ride, explaining the concept of velocity and position functions, and how to calculate distance traveled using antiderivatives. The explanation includes a step-by-step guide on integrating a given function to find the position and then evaluating it at specific points to determine the distance traveled.

05:02

🚴‍♀️ Chloe's Bike Ride Calculations and Personal Anecdotes

The speaker continues the bike ride theme, focusing on Chloe's velocity function provided in piecewise form. They calculate the distance Chloe travels in the first two hours of her ride by finding the antiderivative of her velocity function and evaluating it between the specified time interval. The explanation includes a brief digression into the natural exponential function and its properties. The speaker also shares personal stories, including a song about the quadratic formula and memories of high school band projects, before moving on to analyze Chloe's speed and acceleration at a specific time during her ride.

10:03

🔢 Application of Mean Value Theorem in Velocity Analysis

The speaker addresses a question about finding a time when Brandon's acceleration equals a given value by applying the Mean Value Theorem. They explain the theorem's relevance and demonstrate how to calculate the average rate of change of velocity over a time interval. The speaker confirms the function's continuity and differentiability, which are prerequisites for using the Mean Value Theorem, and concludes that there must be a time when Brandon's acceleration matches the specified value within the given time frame.

15:04

📉 Velocity and Acceleration Relationship in Physics

The speaker explores the relationship between velocity and acceleration, using Chloe's bike ride as an example. They calculate her velocity and acceleration at a specific time and discuss the implications of these values being negative, indicating that her speed is increasing. The explanation includes a general principle that if velocity and acceleration are of the same sign, the speed is increasing, and if they are of opposite signs, the speed is decreasing. The speaker also humorously references buying lottery tickets and shares an anecdote about giving scratch-offs to teachers.

20:04

🤔 Utilizing Intermediate Value Theorem to Compare Velocities

The speaker uses the Intermediate Value Theorem to determine if there is a time when Brandon and Chloe have the same velocity during their respective bike rides. They calculate the difference in their velocities at the beginning and halfway through the ride, noting the change from a positive to a negative value. This indicates that at some point between the start and halfway, their velocities must be equal. The speaker also briefly discusses the difference between velocity and speed, hinting at a deeper conversation on the topic.

Mindmap

Keywords

💡Differentiable

In the context of the video, 'differentiable' refers to a function that has a derivative at every point in its domain. This is a fundamental concept in calculus, signifying that the function has a well-defined rate of change. The script mentions that Brandon's velocity function is differentiable, indicating it can be analyzed for changes in speed over time, which is crucial for understanding his motion dynamics.

💡Velocity Function

A 'velocity function' represents the rate of change of position with respect to time. It is a key concept in kinematics and is central to the video's theme of analyzing motion. The script discusses both Brandon's and Chloe's velocity functions, using them to calculate distances traveled and to understand their motion over time.

💡Piecewise Function

A 'piecewise function' is a function defined by multiple sub-functions, each applicable to a specific interval or condition. In the script, Chloe's velocity function is given as a piecewise function, which allows for different rates of speed change at different times during her bike ride, illustrating the complexity of real-world motion scenarios.

💡Antiderivative

The 'antiderivative', also known as the integral, is the reverse process of differentiation. It is used to find the original function when given its derivative. The script mentions finding the antiderivative of Chloe's velocity function to determine her position function, which is essential for calculating the distance she travels.

💡Position Function

A 'position function' gives the location of an object as a function of time. It is derived from the velocity function by integration. The video script discusses finding Chloe's position function by integrating her velocity function, which helps in determining how far she has traveled at a given time.

💡Acceleration

In the script, 'acceleration' is the rate of change of velocity with respect to time. It is a critical concept in physics and calculus, used to understand how the speed of an object is increasing or decreasing. The video uses the concept of acceleration to analyze Chloe's motion, particularly at the three-hour mark of her bike ride.

💡Mean Value Theorem

The 'Mean Value Theorem' is a theorem in calculus that states if a function is continuous on a closed interval and differentiable on an open interval within that closed interval, then there exists a point at which the function's derivative equals the average rate of change of the function over that interval. The script suggests using this theorem to determine if there is a time when Brandon's acceleration equals a given value.

💡Intermediate Value Theorem

The 'Intermediate Value Theorem' states that if a function is continuous on a closed interval and takes two values, then it takes every value between them at some point in the interval. The video script uses this theorem to justify that there must be a time when Brandon's and Chloe's velocities are equal during their respective bike rides.

💡Continuous Function

A 'continuous function' is a function that does not have any abrupt changes in value, meaning it can be drawn without lifting the pen from the paper. In the script, the continuity of Brandon's velocity function is important for applying the Mean Value Theorem and for understanding the behavior of the function over time.

💡AP Classroom

In the script, 'AP Classroom' refers to a resource for Advanced Placement (AP) students, providing materials to help them prepare for their exams. The video suggests that students should use AP Classroom to review concepts like the Mean Value Theorem, indicating its importance for their studies.

Highlights

Innovative teaching approach where students are required to watch educational videos at home before attending class for practice.

Students are encouraged to put away cell phones to enhance focus and engagement in the classroom.

The concept of PVA (Position, Velocity, Acceleration) is introduced in the context of analyzing Brandon and Chloe's bike ride.

Differentiation between velocity and acceleration is explained through the lens of a bike ride scenario.

Use of a piecewise function to represent Chloe's velocity, emphasizing the importance of selecting the correct piece for analysis.

Explanation of antiderivatives and their application in determining position from velocity functions.

A detailed walkthrough of calculating the antiderivative of a given function to find Chloe's position during her bike ride.

The importance of understanding the natural exponential function in both derivative and integral contexts.

A humorous anecdote about creating a song to help remember the value of e (Euler's number), showcasing the speaker's teaching style.

Application of the mean value theorem to determine if there's a time when Brandon's acceleration equals a given value.

A clear explanation of how to find the average rate of change for a function and its relevance to the mean value theorem.

The intermediate value theorem is introduced to justify the existence of a time when two velocities are equal.

A practical example of using the intermediate value theorem with the velocities of Brandon and Chloe.

The significance of understanding the continuity of functions in calculus and its implications for theorems like the mean value theorem.

A personal story about the speaker's high school experiences, adding a relatable and human touch to the lecture.

A suggestion for students to utilize AP Classroom resources for additional learning and clarification.

The speaker's commitment to continuous improvement and openness to feedback from students.

Transcripts

Browse More Related Video

🚨EXPERT 🚨Tips for How to Get a 💥5 on the 2022 AP Calculus AB Exam💥 [What You REALLY Need to Know]

Calculus AB Homework 5.2: Existence Theorems

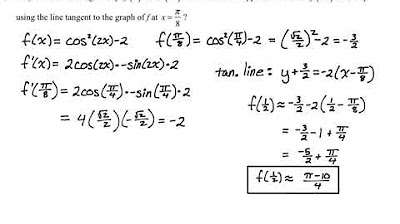
AP Calc AB & BC Practice MC Review Problems #4

2021 Live Review 5 | AP Calculus AB | Understanding the Big Theorems Including IVT, EVT, & MVT

2022 Live Review 5 | AP Calculus AB | Focusing on the Big Theorems Including IVT, EVT, & MVT

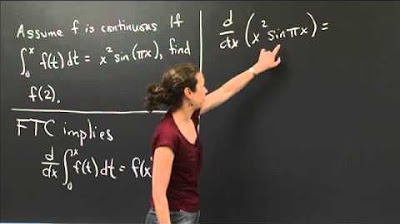
Applying the Second Fundamental Theorem | MIT 18.01SC Single Variable Calculus, Fall 2010

Related Tags

Calculus Velocity Acceleration Biking Education Physics AP Exam Integrals Derivatives Mean Value Theorem Intermediate Value Theorem