Electronic Filters - Vocademy

Vocademy - Electronics Technology

25 Mar 202340:03

EducationalLearning

32 Likes 10 Comments

TLDRThis script delves into the world of electronic filters, explaining the fundamental role of capacitors and inductors in shaping frequency responses within circuits. It covers how capacitors favor high frequencies and inductors favor low frequencies, and how their combinations in series or parallel configurations can create resonant frequencies, acting as band pass or band reject filters. The script further explores various filter types, including RC and RL filters, and introduces more complex filter designs like T, Pi, and H filters, highlighting their applications in audio systems and the importance of cutoff frequency and Q factor in determining filter performance.

Takeaways

📡 Capacitors and inductors have frequency-dependent behavior in AC circuits; capacitors block low frequencies and pass high frequencies, while inductors do the opposite.
🔄 When combined in series, a capacitor and inductor can form a resonant circuit that has high impedance except at the resonant frequency, where impedance is low.
🔄 In parallel, a capacitor and inductor create a circuit with high impedance at the resonant frequency, allowing frequencies near this point to pass while blocking others.
🛠 The addition of resistance to a resonant circuit changes its response, lowering the peak impedance and broadening the frequency range that passes through.
🎚 Filters in electronics allow certain frequencies to pass while blocking others, similar to how mechanical or optical filters operate in their respective domains.
🔊 In audio systems, filters are used to separate frequencies for different speakers, sending low frequencies to woofers and high frequencies to tweeters for optimal sound reproduction.
⚡ The basic building blocks for creating filters are resistors (R), capacitors (C), and inductors (L), which can be arranged to form high pass, low pass, band pass, and band reject filters.
⚙️ The cutoff frequency of an RC or RL filter is determined by the formula f_{ ext{Co}} = \frac{1}{2\pi RC} for RC filters and f_{ ext{Co}} = \frac{R}{2\pi L} for RL filters, where the impedance of the capacitor or inductor equals the resistance.
📊 The frequency response of filters can be visualized on a graph, with a logarithmic scale showing a steady response that drops off sharply at the cutoff frequency.
🔧 The Q factor of a filter, related to its quality, affects the sharpness of the cutoff; a higher Q results in a narrower bandwidth and steeper sides of the filter response curve.
🔄 Series and parallel resonant circuits can be combined to create more complex filters with steeper skirts and broader bandwidths, useful for applications requiring both sharp cutoff and wide frequency range.

Q & A

What is the primary function of a capacitor in an AC circuit?
-A capacitor in an AC circuit tends to block low frequencies and pass high frequencies. It blocks DC and has high impedance at low frequencies, which decreases as the frequency increases.
How does an inductor behave in an AC circuit?
-An inductor in an AC circuit tends to block high frequencies and pass low frequencies. It allows low frequencies to pass through but presents high impedance to high frequencies.
What is the resonant frequency in a series LC circuit?
-The resonant frequency in a series LC circuit is the particular frequency at which the impedance of the inductor and capacitor in series is at its minimum, and they have equal reactance.
How do capacitors and inductors behave when connected in parallel?
-When connected in parallel, capacitors and inductors create a circuit that has high impedance at the resonant frequency where the capacitive and inductive reactances are equal, and lower impedance above and below this frequency.
What is an electronic filter and what does it do?
-An electronic filter is a circuit that allows certain frequencies to pass through while blocking others. It can be designed to filter out specific ranges of frequencies in an electronic signal.
Why are different types of speakers needed for different frequency ranges in an audio system?
-Different types of speakers are needed because low frequencies require a large cone to move a lot of air, while high frequencies require a small cone that can move quickly but doesn't need to move as much air.
What is a low pass filter and how is it created?
-A low pass filter is a type of electronic filter that allows low frequencies to pass through and blocks high frequencies. It can be created by placing a resistor and a capacitor in series, with the capacitor across the signal path.
How can you create a high pass filter?
-A high pass filter can be created by placing a resistor and a capacitor in series, but with the capacitor in series with the signal path. This arrangement allows high frequencies to pass through while blocking low frequencies.
What is the significance of the cutoff frequency in a filter?
-The cutoff frequency is the point at which the filter's response drops to 3 dB below the maximum, or where the power transfer is at 50%. It's the frequency where the impedance of the capacitor equals the resistance in the filter circuit.
How can the Q factor of a filter affect its performance?
-The Q factor, or quality factor, of a filter is a measure of its selectivity. A high Q factor indicates a narrow bandwidth and a steeper filter response, while a low Q factor results in a broader bandwidth and a more gradual response.
What are T, Pi, and H filters, and how do they differ from basic RC or RL filters?
-T, Pi, and H filters are configurations that use combinations of inductors and capacitors to create more complex filter characteristics. They differ from basic RC or RL filters by offering different responses and selectivity, which can be adjusted by tweaking the circuit parameters.

Outlines

00:00

🔌 Capacitors and Inductors in AC Circuits

This paragraph discusses the behavior of capacitors and inductors in AC circuits. Capacitors block low frequencies and pass high frequencies, while inductors do the opposite. When combined in series, they exhibit high impedance except at the resonant frequency, where impedance is low. In parallel, they show high impedance at the resonant frequency with the capacitive and inductive reactances balancing each other out. The paragraph also touches on how adding resistance affects the circuit's response, broadening the frequency range in parallel circuits and narrowing it in series. The concept of electronic filters, which allow certain frequencies to pass while blocking others, is introduced with an analogy to physical filters for liquids and light.

05:01

🎵 Audio Amplifier Systems and Speaker Design

The second paragraph delves into the application of electronic filters in audio amplifier systems, explaining the need for different speaker designs to handle various frequency ranges effectively. Woofers, designed for low frequencies, move more air but require larger cones, while tweeters handle high frequencies with smaller cones that move air quickly. The paragraph outlines a basic concept of a crossover circuit using a resistor and capacitor in series to direct low frequencies to woofers and high frequencies to tweeters, although it acknowledges this is not a practical implementation due to energy waste from the resistor.

10:05

⚡ Understanding RC Filters and Their Frequencies

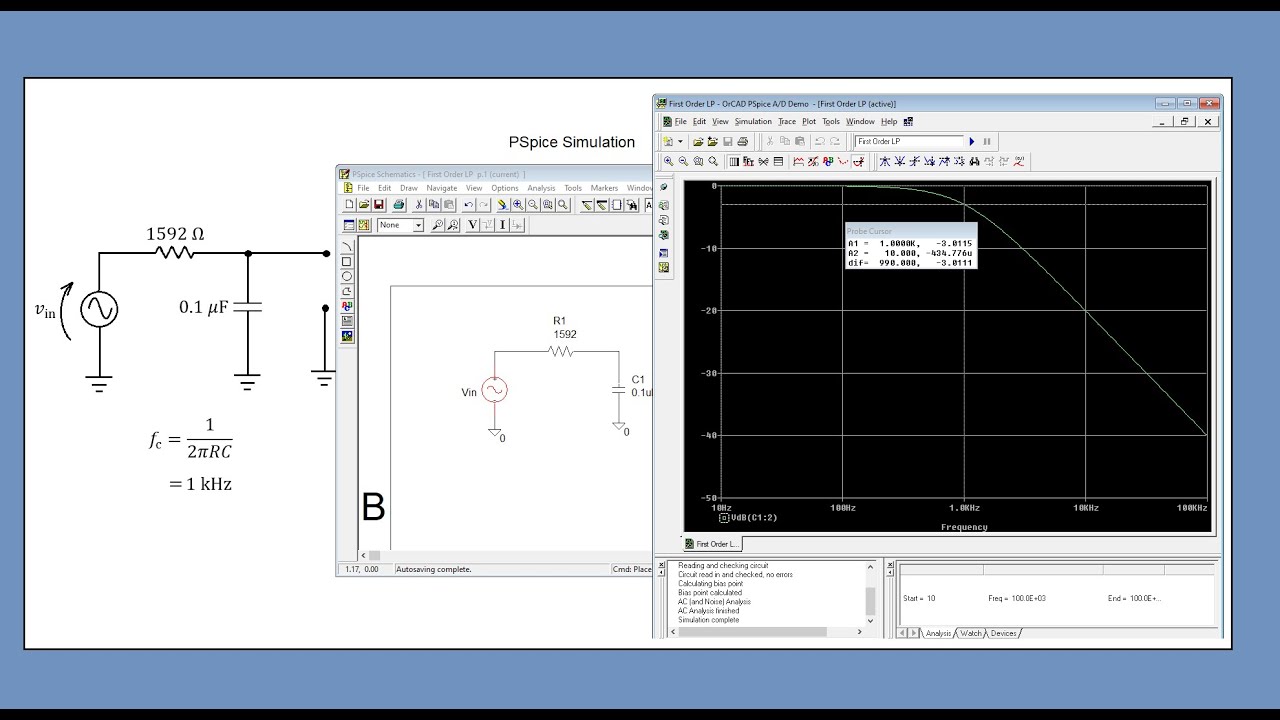
This paragraph explains the fundamentals of RC filters, focusing on how a resistor and capacitor in series affect voltage across them at different frequencies. At low frequencies, the capacitor acts like an open circuit, leading to high voltage across it and low voltage across the resistor. As frequency increases, the voltage across the capacitor decreases, and the resistor's voltage increases. The cutoff frequency is identified as the point where the voltages across both components are equal, and the formula for calculating the cutoff frequency of an RC filter is provided.

15:05

📊 Graphing Frequency Response of Filters

The fourth paragraph discusses how to graphically represent the frequency response of filters, using a logarithmic scale to illustrate the steady response until the cutoff frequency is reached, after which the response drops off. The cutoff frequency is defined as the point where the power transfer is 50% (3 dB below the peak), and the importance of this point in determining the filter's performance is emphasized. The paragraph also explains how the orientation of the resistor and capacitor in the circuit determines whether it is a high pass or low pass filter.

20:09

🌀 Inductors in Filters and RL Filter Calculations

The role of inductors in filters is explored in this paragraph, which is similar to capacitors but inverse in their effect on frequency—inducing low frequencies and blocking high frequencies. The concept of RL filters is introduced, and the formula for calculating the cutoff frequency of an RL filter is provided, which is based on the inductive reactance being equal to the resistance at the cutoff frequency.

25:09

📛 Band Pass and Band Reject Filters with Resonant Circuits

This paragraph introduces band pass and band reject filters, which are created using resonant circuits. A series resonant circuit acts as a band pass filter, allowing the resonant frequency to pass through with high impedance at low and high frequencies. A parallel resonant circuit functions as a band reject filter, blocking the resonant frequency while allowing frequencies above and below to pass. The impact of resistance on the filter's bandwidth and the Q factor is also discussed.

30:15

🔄 Exploring Different Resonant Circuit Configurations

The sixth paragraph examines various resonant circuit configurations, such as series and parallel resonant circuits, and their effects on filtering frequencies. It explains how these configurations can be arranged in series or parallel with the signal to create band pass or band reject filters. The resonant frequency's role in determining the filter's behavior is highlighted, along with the impact of resistance on the filter's response curve.

35:15

🛠 Advanced Filter Configurations: T, Pi, and H Filters

This paragraph delves into more complex filter configurations, such as T, Pi, and H filters, which offer different characteristics compared to simple LC or RC filters. These configurations can be adjusted to achieve specific filter responses, although the detailed design process is beyond the scope of the discussion. The paragraph also touches on the possibility of combining resonant circuits to create filters with steeper skirts and broader bandwidths.

🔍 Broadening and Steepening Filter Responses

The final paragraph discusses the trade-off between steepness and bandwidth in filters, and how adding resistance can affect the filter's response. It suggests that while a high Q filter has a narrow bandwidth and steep sides, adding resistance can broaden the bandwidth at the expense of steepness. The paragraph concludes by hinting at the possibility of designing filters with both steep skirts and wide bandwidths for specific applications.

Mindmap

Keywords

💡Capacitors

Capacitors are electronic components that store electrical energy in an electric field. They are characterized by their ability to block direct current (DC) while allowing alternating current (AC) to pass, with a tendency to pass high frequencies and block low frequencies. In the video, capacitors are discussed in the context of AC circuits and their role in filtering, where they can be used to create high-pass or low-pass filters depending on their configuration with resistors.

💡Inductors

Inductors are components that store energy in a magnetic field. They oppose changes in electric current and have the property of allowing low frequencies to pass while blocking high frequencies in AC circuits. The video explains how inductors, similar to capacitors, can be used in series or parallel configurations to create filters that either pass or block specific frequency ranges.

💡Resonant Frequency

Resonant frequency is the particular frequency at which a circuit, consisting of an inductor and capacitor, exhibits a minimum impedance. In the script, the resonant frequency is described as the point where the impedance of a series LC circuit is at its lowest, allowing the circuit to act like a short circuit for that frequency, which is crucial for understanding how series and parallel resonant circuits function as filters.

💡Impedance

Impedance is the measure of the opposition that a circuit presents to a current when a voltage is applied. In the context of the video, impedance is discussed in relation to how it changes with frequency in series and parallel LC circuits, affecting the circuit's behavior as a filter at different frequencies.

💡Electronic Filters

Electronic filters are circuits that allow certain frequencies to pass while blocking others. The video script delves into various types of electronic filters, such as low-pass, high-pass, band-pass, and band-reject filters, explaining how they can be constructed using combinations of capacitors, inductors, and resistors.

💡Cutoff Frequency

The cutoff frequency is the point at which the filter's output power is reduced to half (3 dB down) from its peak value. It is a critical parameter in filter design, determining the frequency at which the filter transitions from passing to blocking signals. The script explains how to calculate the cutoff frequency for RC and RL filters.

💡Audio Amplifier System

An audio amplifier system is used to increase the amplitude of an audio signal, often requiring filters to separate different frequency ranges for speakers designed to reproduce specific parts of the audio spectrum. The script uses the example of an audio amplifier system to illustrate the practical application of filters, such as sending low frequencies to woofers and high frequencies to tweeters.

💡Reactance

Reactance is the opposition to the flow of alternating current (AC) due to capacitance or inductance in a circuit. Capacitive reactance decreases with increasing frequency, while inductive reactance increases. The video discusses reactance in the context of how it affects the operation of filters at various frequencies.

💡RL and RC Filters

RL and RC filters refer to circuits that use resistors and inductors (RL) or resistors and capacitors (RC) to create low-pass or high-pass filtering effects. The script explains how these filters are designed, their frequency response, and how they can be arranged to achieve the desired filtering characteristics.

💡Bandwidth

Bandwidth is the range of frequencies that a filter allows to pass through. The script discusses how the bandwidth of a filter can be adjusted by adding resistance, which affects the steepness of the filter's response curve and its ability to isolate specific frequency ranges.

💡Q Factor

The Q factor, or quality factor, is a measure of the selectivity of a filter, indicating how narrow or broad the passband is. A high Q factor means a narrow bandwidth with steep filter skirts, while a low Q factor results in a broader bandwidth. The script mentions Q factor in relation to the design of resonant circuit filters.

Highlights

Capacitors tend to block low frequencies and pass high frequencies in AC circuits, while inductors do the opposite.

Inductors and capacitors in series exhibit a resonant frequency where impedance is at its minimum.

Parallel combination of inductors and capacitors results in high impedance at the resonant frequency.

Filters can be designed to pass or block specific frequencies, similar to how physical filters work.

Audio amplifier systems use filters to separate low and high frequencies for woofers and tweeters respectively.

RC series circuit demonstrates how low frequencies create high voltage across the capacitor and low voltage across the resistor.

High frequencies in an RC series circuit result in low voltage across the capacitor and high voltage across the resistor.

The concept of a crossover circuit to divert high frequencies to tweeters and low frequencies to woofers is introduced.

Practical limitations of using resistors in crossover circuits due to energy wastage are discussed.

Introduction to the idea of electronic filters, which allow certain frequencies to pass while blocking others.

Explanation of how to create a low pass filter using a resistor and capacitor in parallel.

The formula for calculating the cutoff frequency of an RC filter is derived as 1 / (2πRC).

Cutoff frequency is defined as the point where power transfer drops by three decibels or 50 percent.

Filters can be designed as high pass, low pass, band pass, or band reject based on circuit configuration.

RL filters, similar to RC filters, use inductors and resistors to create high pass and low pass filters.

Resonant circuits, both series and parallel, can create band pass or band reject filters depending on their configuration.

T, Pi, and L filters are introduced as more complex configurations that can be adjusted for specific filter characteristics.

H filters, resembling the letter H, are mentioned as another advanced filter configuration.

The impact of resistance on filter Q factor and bandwidth is explained, affecting the steepness and width of the filter response.

Complex filters combining series and parallel resonant circuits can achieve both steep skirts and a wide bandwidth.

Transcripts

Browse More Related Video

Topic 26: Bode Plots (and a little PSpice)

Inductors Explained - The basics how inductors work working principle

12. LCR Circuits—DC Voltage

What is a Capacitor? (Physics, Electricity)

02 - Overview of Circuit Components - Resistor, Capacitor, Inductor, Transistor, Diode, Transformer

All electronic components names, functions, testing, pictures and symbols - smd components

Related Tags

Electronic Filters AC Circuits Capacitors Inductors Resonant Frequency Audio Amplifiers Signal Processing Cutoff Frequency Series Resonance Parallel Resonance