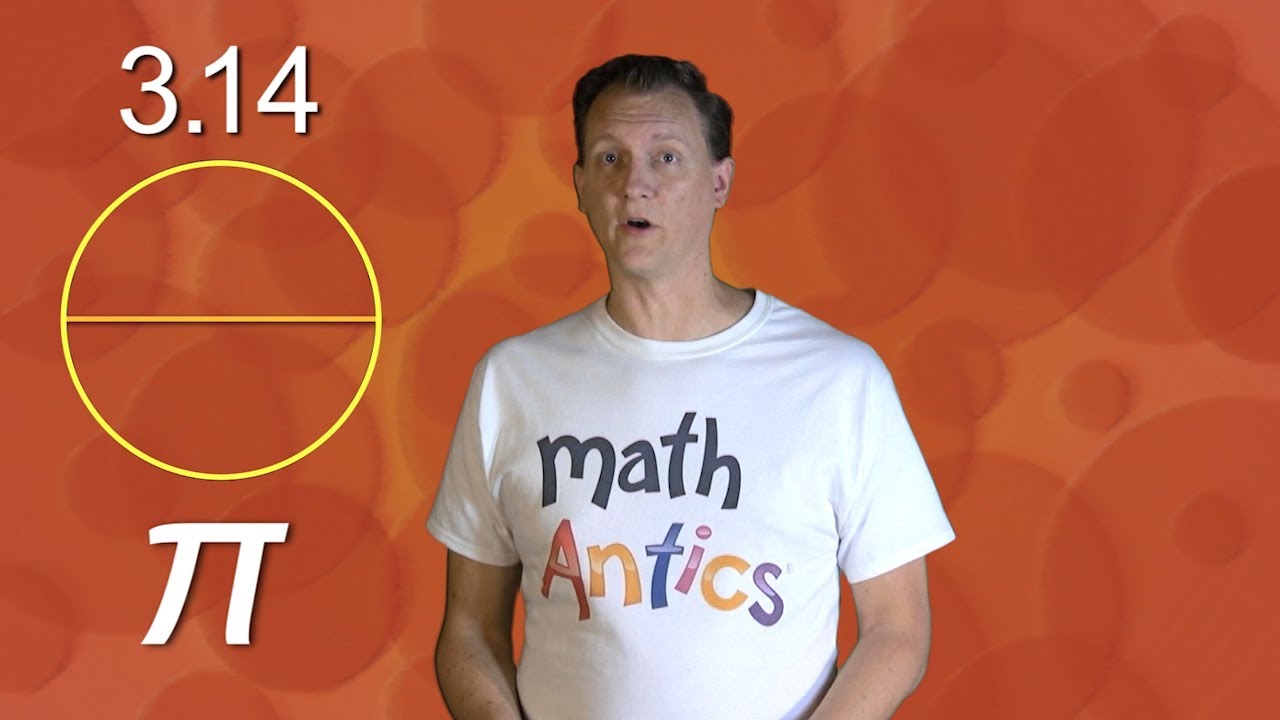The infinite life of pi - Reynaldo Lopes
TLDRThis script explores the fascinating history and significance of pi, the constant ratio of a circle's circumference to its diameter. It delves into its discovery, its use in ancient civilizations, and its role in various scientific fields. Pi, an irrational number with a never-ending decimal sequence, is symbolized by the Greek letter and is crucial for calculations involving circles, oscillating systems, and even the density of the universe. The script highlights the computational feats of calculating pi to trillions of digits and its memorization records, showcasing its pervasiveness in diverse scientific applications.
Takeaways
- 📏 Measuring a circle's diameter and radius is straightforward with a ruler, but the circumference requires a flexible measuring tool.
- 🔍 The circumference of a circle is directly proportional to its diameter, with a constant ratio regardless of the circle's size.
- 📚 The concept of this ratio, known as pi, has been known for nearly 4,000 years, with historical mentions in various ancient civilizations.
- 🏛 Pi was potentially used in the construction of the Egyptian pyramids, highlighting its long-standing significance in geometry.
- ⚙️ Ancient mathematicians estimated pi by inscribing polygons within circles, and by 1400, it was calculated to ten decimal places.
- 🔢 Pi is an irrational number, meaning it cannot be expressed as a ratio of two whole numbers and its decimal representation is infinite.
- 📈 The decimal expansion of pi starts with 3.14159 and continues indefinitely, which is why we use the Greek letter π as a shorthand.
- 💻 Modern technology, including quantum computers, has been used to calculate pi to an astonishing two quadrillion digits.
- 🧠 Memorization contests and records for pi exist, with some individuals memorizing over 67,000 digits.
- 🔬 Scientific applications of pi are extensive, including calculations for the volume of a soda can and the orbits of satellites.
- 🎵 Pi is also relevant in understanding periodic systems such as clocks, electromagnetic waves, and even music.
- 📊 In statistics, pi is integral to calculating areas under the normal distribution curve, which is used for various distributions and models.
- 🌌 Pi plays a role in particle physics experiments, such as those at the Large Hadron Collider, due to its relevance in particle orbits.
- 🌌 The density of the universe, though vast, contains fewer elements than the digits in pi, emphasizing the number's infinite nature.
Q & A
What is the easiest way to measure the diameter and radius of a circle?
-The diameter and radius of a circle can be easily measured using a straight ruler, as they are straight lines.
Why might one need a measuring tape or a piece of string to measure a circle's circumference?
-A measuring tape or a piece of string is needed to measure the circumference of a circle because it is not a straight line, unlike the diameter and radius.
What is the constant ratio between a circle's circumference and its diameter?
-The constant ratio between a circle's circumference and its diameter is known as pi, represented by the Greek letter π.
How long has the concept of pi been known to humanity?
-The concept of pi has been known for almost 4,000 years, appearing in the works of ancient Greek, Babylonian, Chinese, and Indian mathematicians.
How did ancient mathematicians estimate the value of pi?
-Ancient mathematicians estimated the value of pi by inscribing polygons in circles and calculating the perimeter of these polygons.
Why is pi considered an irrational number?
-Pi is considered an irrational number because it cannot be expressed as a ratio of two whole numbers and its decimal representation goes on infinitely without repeating.
What is the significance of pi in modern computing?
-In modern computing, pi is used to test the speed of computers, with quantum computers being able to calculate it up to two quadrillion digits.
What is the practical limit of pi's decimal places for most scientific uses?
-For most scientific uses, only the first forty decimal places of pi are needed.
In what fields is pi used in scientific calculations?
-Pi is used in various fields, including calculations involving circles, such as the volume of a can of soda, the orbits of satellites, and in studying curves, periodic or oscillating systems, and in statistics.
How is pi used in particle physics experiments?
-In particle physics experiments, such as those using the Large Hadron Collider, pi is used due to its relevance in understanding the orbits in which tiny particles move.
What is one of the most impressive uses of pi mentioned in the script?
-One of the most impressive uses of pi mentioned in the script is its application in calculating the density of our entire universe.
Outlines
📏 The Mystery of Pi: Measuring the Circle
This paragraph delves into the challenge of measuring a circle, particularly its circumference, which cannot be done with a ruler but requires a measuring tape or string. It explains the fundamental relationship between a circle's circumference and its diameter, a ratio that remains constant regardless of the circle's size. This ratio is identified as the irrational number pi, which has been known for nearly 4,000 years and was estimated by ancient mathematicians through the method of inscribing polygons. The paragraph also touches on the historical use of pi in the construction of the Egyptian pyramids and the progression in calculating its value to ten decimal places by the year 1400. It clarifies that pi's value is an infinite, non-repeating decimal, which is why it is symbolized by the Greek letter pi. The modern significance of pi in computing speed tests and memorization contests is mentioned, along with its practical applications in various scientific fields, including satellite orbits, curve studies, periodic systems, statistics, and particle physics.
Mindmap
Keywords
💡Circle
💡Diameter
💡Radius
💡Circumference
💡Ratio
💡Pi (π)
💡Irrational Number
💡Polygons
💡Quantum Computers
💡Scientific Uses
💡Normal Distribution
💡Large Hadron Collider
Highlights
Measuring a circle involves using a ruler for diameter and radius, and a measuring tape or string for the circumference.
The circumference of a circle changes proportionally with its diameter.
The ratio of a circle's circumference to its diameter is a constant number, regardless of the circle's size.
This constant ratio is known as pi, and has been known for approximately 4,000 years.
Estimates of pi appear in ancient Greek, Babylonian, Chinese, and Indian mathematical works.
Pi is believed to have been used in the construction of the Egyptian pyramids.
Mathematicians estimated pi by inscribing polygons in circles.
By 1400, pi had been calculated to ten decimal places.
Pi is an irrational number and cannot be expressed as a ratio of two whole numbers.
The decimal representation of pi starts with 3.14159 and continues infinitely.
Pi is commonly referred to using the Greek letter 'π'.
Modern computers, including quantum computers, calculate pi to an unprecedented number of digits.
People compete to memorize digits of pi, with records exceeding 67,000 digits.
For most scientific uses, the first forty digits of pi are sufficient.
Pi is used in various calculations involving circles, such as the volume of a soda can.
Pi is also useful in studying curves and periodic systems like clocks and electromagnetic waves.
In statistics, pi is used in equations to calculate areas under normal distribution curves.
Pi is utilized in particle physics experiments, including those at the Large Hadron Collider.
Scientists have used pi to demonstrate the dual nature of light as both a particle and an electromagnetic wave.
Pi has been instrumental in calculating the density of the universe.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: