Calculus - The chain rule for derivatives

MySecretMathTutor
22 Sept 201307:09
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial delves into the intricacies of the chain rule for derivatives, a fundamental concept for differentiating composite functions. The instructor emphasizes the importance of identifying the outer and inner functions and applies the chain rule formula step-by-step through various examples, such as differentiating (x^2 + 1)^3, √(5x - 3), and e^(x^2 - 1). The video offers clear guidance on when to use the chain rule, highlighting its distinction from the product rule and providing tips for recognizing and applying the rule effectively.

Takeaways
  • πŸ“š The Chain Rule is a derivative rule used for the composition of two functions, where one function is nested within another.
  • πŸ” To apply the Chain Rule, identify the outer and inner functions in the given expression and differentiate them accordingly.
  • πŸ“ The formula for the Chain Rule is \( (F(G(x)))' = F'(G(x)) \cdot G'(x) \), where \( F \) is the outer function and \( G \) is the inner function.
  • πŸ“ When using the Chain Rule, the derivative of the inner function remains unchanged, and it is multiplied by the derivative of the outer function.
  • ⚠️ The Chain Rule is specifically for function compositions, not for multiplication of functions, which would require the Product Rule.
  • 🧩 In the example of differentiating \( (x^2 + 1)^3 \), the outer function is the cubing, and the inner function is \( x^2 + 1 \).
  • πŸ“‰ For the square root of \( 5x - 3 \), the outer function is the square root (considered as raising to the power of 1/2), and the inner function is \( 5x - 3 \).
  • πŸ”‘ In the example of \( 4x + e^{x^2 - 1} \), the Chain Rule is used for the exponential part where \( x^2 - 1 \) is the inner function nested within \( e \) to the power of that expression.
  • πŸ“ˆ The derivative of the outer function is brought down, the inner function remains the same, and then it is multiplied by the derivative of the inner function.
  • πŸ“ It's crucial to clean up the expression after applying the Chain Rule to make it easier to understand and simplify if possible.
  • 🌐 For more examples and tutorials, the video suggests visiting the website 'mysecretmathtutor.com'.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the chain rule for derivatives in calculus.

  • What is the chain rule used for in calculus?

    -The chain rule is used for finding the derivative of a function that is composed of two or more functions, i.e., when one function is nested inside another.

  • What is the first step in applying the chain rule?

    -The first step in applying the chain rule is to take the derivative of the outside function with the inside function plugged in.

  • How is the inside function treated when applying the chain rule?

    -The inside function remains unchanged when applying the chain rule, and then it is multiplied by its own derivative.

  • What is an example of a situation where the chain rule is not applicable?

    -The chain rule is not applicable when functions are being multiplied, as that situation requires the product rule instead.

  • What is the derivative of (x^2 + 1)^3 according to the video?

    -The derivative of (x^2 + 1)^3 is 3(x^2 + 1)^2 * (2x), which simplifies to 6x(x^2 + 1)^2.

  • How is the square root function treated as a power when finding its derivative?

    -The square root function is treated as a power of one-half, which allows the application of the power rule for differentiation.

  • What is the derivative of the square root of 5x - 3, as shown in the video?

    -The derivative of the square root of 5x - 3 is (5/2) * sqrt(5x - 3).

  • In the video, how is the chain rule applied to the function 4x + e^(x^2 - 1)?

    -The chain rule is applied by taking the derivative of 4x and the derivative of e^(x^2 - 1), where the latter uses the chain rule with e^x as the outside function and x^2 - 1 as the inside function, resulting in 4 + 2x * e^(x^2 - 1).

  • What is the importance of identifying the outside and inside functions when using the chain rule?

    -Identifying the outside and inside functions is crucial for correctly applying the chain rule, as it determines which parts of the function to differentiate and how to combine them.

  • What is the final derivative given in the video for the function 4x + e^(x^2 - 1)?

    -The final derivative for the function 4x + e^(x^2 - 1) is 4 + 2x * e^(x^2 - 1).

  • Why is it important to keep the inside function unchanged when applying the chain rule?

    -Keeping the inside function unchanged is important because it ensures that the derivative of the inside function is correctly multiplied by the derivative of the outside function, as per the chain rule formula.

  • What is the website mentioned in the video for more math tutorials?

    -The website mentioned in the video for more math tutorials is mysecretmathtutor.com.

Outlines
00:00
πŸ“š Introduction to the Chain Rule for Derivatives

This paragraph introduces the concept of the chain rule in calculus, which is a fundamental principle for finding the derivative of a composite function. The explanation emphasizes the importance of identifying the outer and inner functions involved in the composition. The formula for the chain rule is presented, highlighting the process of taking the derivative of the outer function with the inner function plugged in, and then multiplying by the derivative of the inner function. The paragraph also clarifies that the chain rule is specifically for compositions, not for products, and provides a tip on keeping the inner function unchanged while calculating the derivative.

05:01
πŸ” Applying the Chain Rule with Examples

This paragraph delves into applying the chain rule with specific examples to illustrate the process. The first example involves differentiating a function that is the cube of (x^2 + 1), where the outer function is cubing and the inner function is (x^2 + 1). The explanation shows the step-by-step process of taking the derivative of the outer function, keeping the inner function the same, and then multiplying by the derivative of the inner function. The second example demonstrates the derivative of the square root of (5x - 3), where the square root is treated as the outer function raised to the power of one-half, and the inner function is (5x - 3). The process is explained in detail, including simplifying the expression to find the final derivative. The paragraph concludes with a more complex example involving an exponential function, emphasizing the need to correctly identify the outer and inner functions to apply the chain rule correctly.

Mindmap
Keywords
πŸ’‘Chain Rule
The Chain Rule is a fundamental concept in calculus for finding the derivative of a composite function, where a function is composed of two or more functions nested within each other. It is central to the video's theme as it is the main rule being explained and demonstrated through various examples. In the script, the Chain Rule is used to differentiate expressions like (x^2 + 1)^3 and √(5x - 3), illustrating how to break down the problem into simpler parts and apply the rule accordingly.
πŸ’‘Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. It is the main focus of the video, as the Chain Rule is a method for finding derivatives of composite functions. The script provides examples of derivatives being calculated using the Chain Rule, such as the derivative of x^2 + 1 cubed, which is explained step by step to show the process of differentiation.
πŸ’‘Composition of Functions
The composition of functions refers to the process of applying one function to the result of another. It is a key concept in the Chain Rule, as the rule is specifically used for differentiating composite functions. The script explains that the Chain Rule is only used when functions are composed, not when they are simply multiplied, which would require a different rule, such as the Product Rule.
πŸ’‘Outside Function
In the context of the Chain Rule, the 'outside function' is the function that is applied to the result of the 'inside function'. The script emphasizes the importance of identifying the outside function when applying the Chain Rule, as it is the first part of the composite function to differentiate. For example, in the expression (x^2 + 1)^3, cubing is the outside function.
πŸ’‘Inside Function
The 'inside function' is the function that is nested within the outside function in a composite function. Identifying the inside function is crucial for applying the Chain Rule correctly. In the script, the inside function in the example (x^2 + 1)^3 is x^2 + 1, and its derivative is calculated as part of the process.
πŸ’‘Power Rule
The Power Rule is a basic principle in calculus for finding the derivative of a function raised to a power. It is used in the video when differentiating the outside function of a composite function. For instance, when differentiating (x^2 + 1)^3, the Power Rule is applied to the outside function, x^3, by bringing down the exponent and reducing it by one.
πŸ’‘Product Rule
The Product Rule is another derivative rule in calculus for multiplying two functions. It is mentioned in the script to contrast with the Chain Rule, clarifying that the Chain Rule is for compositions, not for products. The script notes that if functions are being multiplied, the Product Rule should be used instead of the Chain Rule.
πŸ’‘Square Root
A square root is a mathematical operation that finds a number which, when multiplied by itself, gives the original number. In the video, the square root is used as an example of an outside function when differentiating √(5x - 3). The script explains how to rewrite the square root as a power of one-half to apply the Chain Rule.
πŸ’‘Exponential Function
An exponential function is a function where the variable is in the exponent. The video script includes an example of differentiating an exponential function, e^(x^2 - 1), using the Chain Rule. It demonstrates the process of identifying the inside function (x^2 - 1) and applying the derivative of the exponential function (e^x) to it.
πŸ’‘Sum Rule
The Sum Rule in calculus allows for the differentiation of a sum of functions by differentiating each function separately and then adding the results. The script mentions the Sum Rule in the context of differentiating 4x + e^(x^2 - 1), where the derivative of each term is calculated individually before applying the Chain Rule to the exponential part.
Highlights

Introduction to the chain rule for derivatives, a fundamental concept in calculus.

Explanation of the chain rule's applicability to the composition of two functions.

The formula for the chain rule is presented with an emphasis on its structure and components.

Tips on identifying and applying the chain rule to nested functions.

Clarification that the chain rule is not for multiplication but for compositions of functions.

The importance of recognizing the 'inside' and 'outside' functions in the chain rule process.

Demonstration of the chain rule with the derivative of x squared plus 1 cubed.

Step-by-step breakdown of the derivative process for a composite function involving exponentiation.

Use of the power rule in conjunction with the chain rule for a clearer understanding.

The derivative of the square root of 5x minus 3, illustrating the chain rule with a root function.

Conversion of the square root to a fractional exponent to simplify the derivative process.

Derivative of an exponential function with a nested quadratic expression inside.

Application of the sum rule for derivatives alongside the chain rule for complex functions.

Identification of the exponential function as the 'outside' and the quadratic as the 'inside' in a composite function.

Final expression for the derivative of an exponential function with a nested quadratic, emphasizing clarity.

Encouragement to visit the website for more educational content on calculus and derivatives.

Transcripts

Browse More Related Video

Chain rule | Derivative rules | AP Calculus AB | Khan Academy

The Chain Rule

Worked example: Derivative of Ã(3x_-x) using the chain rule | AP Calculus AB | Khan Academy

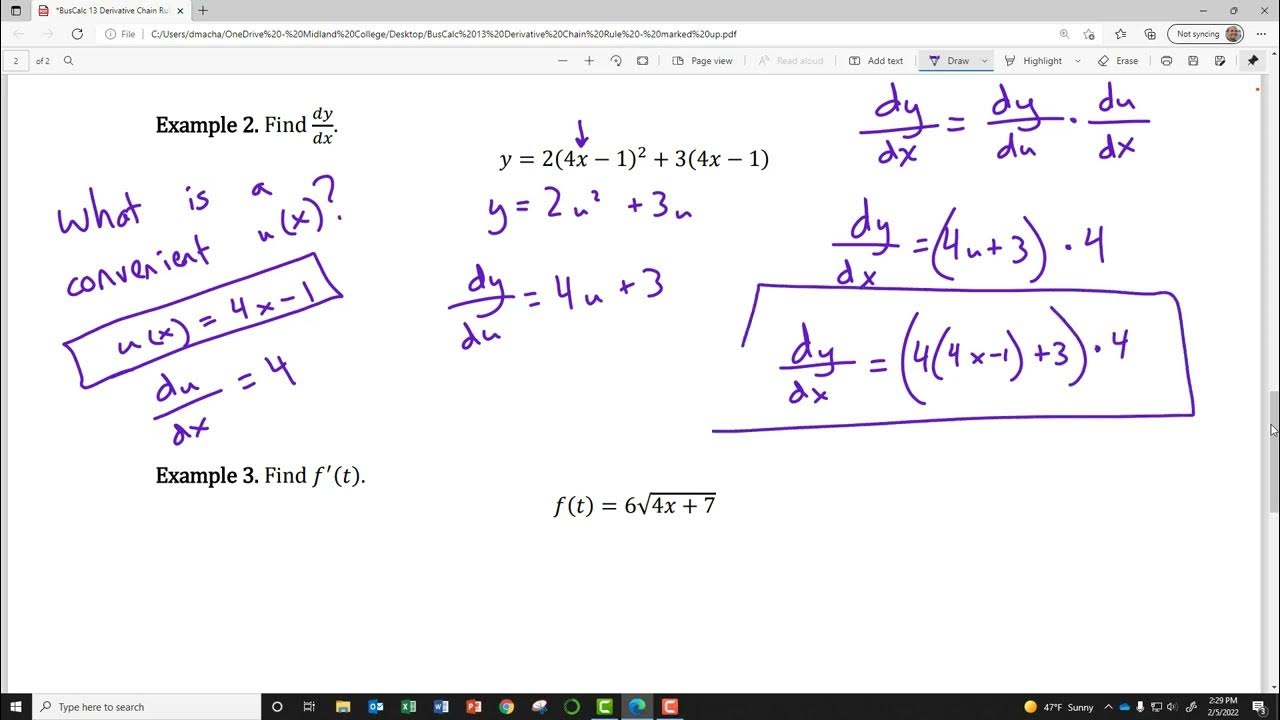
BusCalc 13 Derivative Chain Rule

Chain Rule: the Derivative of a Composition

Applying the chain rule twice | Advanced derivatives | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Chain RuleDerivativesMath TutorFunction CompositionEducational VideoMathematicsCalculus TipsTrigonometryAlgebraLearning Resource