8.01x - Lect 15 - Momentum, Conservation of Momentum, Center of Mass

Lectures by Walter Lewin. They will make you ♥ Physics.

8 Feb 201552:17

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture introduces the concept of momentum in physics, explaining it as the product of an object's mass and velocity. The instructor discusses how momentum is conserved when no external forces act on a system, using examples like star clusters and particle interactions. Through various demonstrations, including explosions and collisions on an air track, the video illustrates the difference between conserved momentum and variable kinetic energy. The script also covers the center of mass, showing its uniform motion in the absence of external forces and its importance in understanding an object's overall movement.

Takeaways

🌟 Momentum is a vector quantity in physics, defined as the product of an object's mass and velocity, with units of kilogram meters per second.
🔍 According to Newton's second law, force is the rate of change of momentum with respect to time (F = dp/dt), implying that a force causes a change in momentum.
💥 In a system of interacting particles, such as a star cluster, internal forces between particles cancel each other out when considering the system as a whole, leading to the conservation of momentum.
🚀 The conservation of momentum principle states that the total momentum of a system remains constant if the sum of all external forces acting on the system is zero.
🧲 Internal forces within a system, such as gravitational or electrical interactions, do not affect the total momentum of the system when external forces are absent.
🎯 An example of conservation of momentum is observed in collisions where the total momentum before and after the collision remains the same, even though individual objects may stick together or bounce off each other.
⚡ The difference between kinetic energy and momentum is highlighted by the fact that kinetic energy can change, increase, or decrease during collisions due to internal forces, while momentum remains conserved in the absence of external forces.
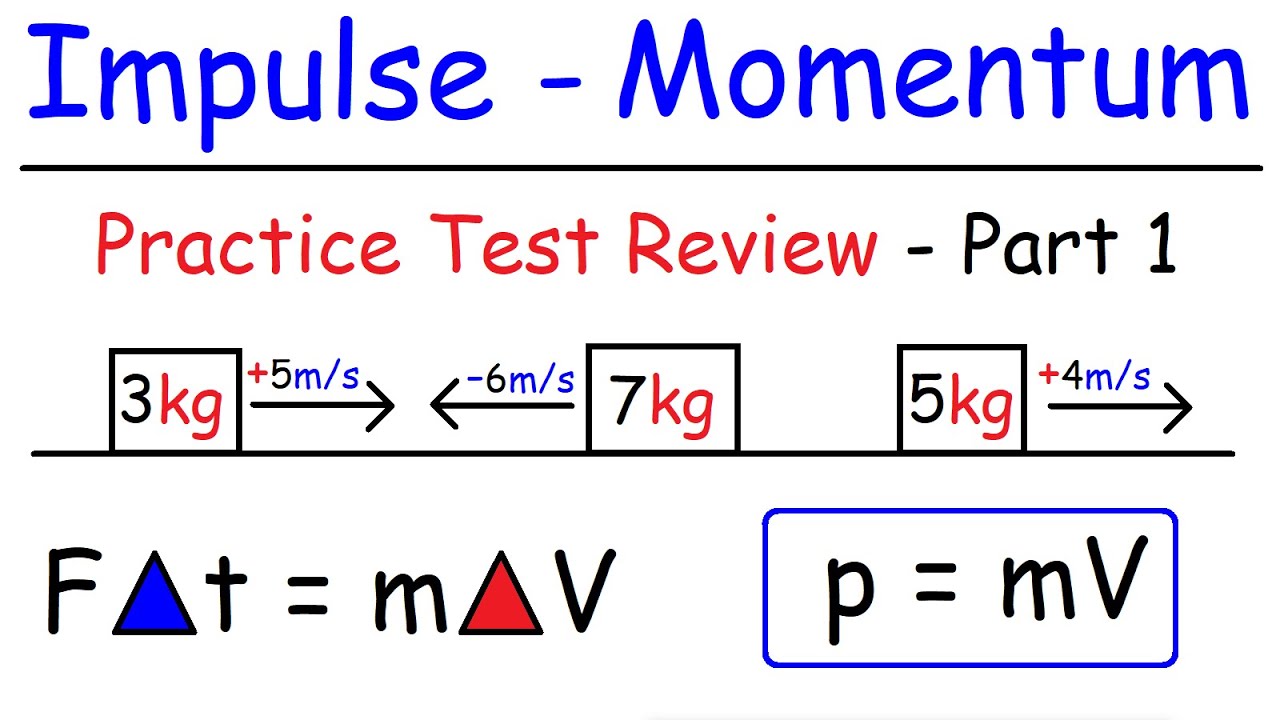
📚 The script provides a numerical example of a one-dimensional collision between two objects, demonstrating how to calculate the velocity after the collision using conservation of momentum.
🔬 The concept of kinetic energy being converted or transferred during collisions and explosions is explained, with kinetic energy potentially decreasing or increasing, unlike momentum, which is always conserved.
📐 The script introduces the concept of the center of mass of an object, which is the point at which the total mass of the object can be considered to be concentrated for the purpose of analyzing its motion, especially under the influence of external forces.
🧭 The behavior of the center of mass is such that it moves as if all the mass of the object were concentrated at this point, making it a useful concept for predicting the motion of objects under various conditions.

Q & A

What is the concept of momentum in physics?
-In physics, momentum is a vector quantity that represents the product of the mass of a particle and its velocity. It is measured in units of kilograms times meters per second.
How is momentum related to force according to the principle F = ma?
-According to the principle F = ma (force equals mass times acceleration), force can also be expressed as the rate of change of momentum with respect to time, which is written as F = dp/dt, where p is momentum.
What does it mean for the internal forces between particles to cancel each other out in a system?
-When considering the system as a whole, the internal forces between particles, such as gravitational or electrical interactions, cancel each other out because for every action, there is an equal and opposite reaction according to Newton's Third Law.
What is the conservation of momentum and under what condition does it hold?
-The conservation of momentum states that if the total external force acting on a system is zero, the total momentum of the system cannot change. This principle holds true regardless of the internal interactions between the particles within the system.
How does the conservation of momentum apply to a collision between two objects?
-In a collision, the total momentum of the system before the collision must be equal to the total momentum after the collision, assuming no external forces act on the system. This principle allows us to calculate the velocities of the objects after the collision.
What is the difference between momentum and kinetic energy in the context of a collision?
-While momentum is a measure of motion that is conserved in the absence of external forces, kinetic energy is the energy of motion that can change during a collision. It is possible for kinetic energy to decrease or even be completely converted into other forms of energy during an inelastic collision, whereas momentum remains constant.
Can kinetic energy increase during a collision?
-Kinetic energy can increase during certain types of events, such as an explosion, where potential energy is converted into kinetic energy. However, in traditional collisions, especially inelastic collisions, kinetic energy typically decreases or is converted into other forms of energy.
What is the center of mass of a system and how is it defined?
-The center of mass of a system is the point at which the total mass of the system can be considered to be concentrated. It is defined as the average position of all the mass elements of the system, such that the total mass times the position vector of the center of mass equals the sum of the individual masses times their position vectors.
How does the motion of the center of mass behave when there are no external forces acting on a system?
-In the absence of external forces, the center of mass of a system moves with a constant velocity. It does not accelerate and maintains a uniform motion, regardless of the individual motions or orientations of the objects within the system.
What is the significance of the center of mass in understanding the motion of an object?
-The center of mass is significant because it simplifies the analysis of an object's motion. The behavior of the center of mass is predictable and uniform, making it easier to understand and calculate the overall motion of an object, especially when the object is rotating or tumbling.
How can the concept of momentum be demonstrated experimentally?
-The concept of momentum can be demonstrated experimentally using an air track, where two objects with known masses are connected by a spring. When the spring is released, the objects move apart with velocities that conserve the total momentum of the system, allowing for direct observation and measurement of momentum conservation.

Outlines

00:00

🚀 Introduction to Momentum and Conservation Laws

The script begins with an introduction to the concept of momentum in physics, explaining it as a vector quantity that is the product of an object's mass and velocity, with units of kilograms times meters per second. It delves into the relationship between force and momentum, highlighting Newton's second law (F = ma) and how it relates to the rate of change of momentum (dp/dt). The lecturer then explores the behavior of momentum in systems of interacting particles, such as a star cluster, emphasizing that internal forces between particles cancel each other out, leading to the conclusion that the total external force on a system dictates the change in its total momentum. The conservation of momentum is introduced as a principle that holds when the total external force on a system is zero.

05:00

🌌 Conservation of Momentum in Clusters and Collisions

This paragraph expands on the concept of momentum conservation, particularly in the context of celestial bodies like star clusters and during collisions. It uses the example of a globular cluster to illustrate that internal forces, such as gravitational interactions between stars, do not affect the total momentum of the cluster. The lecturer then presents a simple numerical example involving a one-dimensional collision between two objects of different masses and velocities, demonstrating how the conservation of momentum principle can be used to calculate the velocity of the objects after they collide and stick together. The example underscores the idea that while individual momenta change due to internal forces, the total momentum of the system remains constant if there are no external forces at play.

10:02

💥 The Difference Between Momentum and Kinetic Energy

The script contrasts momentum and kinetic energy, highlighting that while momentum is always conserved in the absence of external forces, kinetic energy can change during collisions. It presents a thought experiment involving a head-on collision that results in a significant loss of kinetic energy, emphasizing that kinetic energy can be destroyed while momentum remains constant. The lecturer also discusses explosions as a scenario where kinetic energy increases due to internal forces, such as chemical reactions, while momentum is still conserved. The importance of not confusing the two concepts is stressed, as they behave differently under the influence of forces.

15:03

🔍 Experimental Demonstration of Momentum Conservation

The script describes an experimental setup to demonstrate the conservation of momentum using an air track and two cars connected by a spring. The experiment is designed to show that when the spring is released, the cars move in opposite directions with velocities that are inversely proportional to their masses, thus conserving the total momentum of the system. The lecturer explains the method of measuring the speed of the cars by timing how long it takes for them to travel a fixed distance and predicts that the times for cars of equal mass should be the same within the uncertainty of the measurements. The paragraph concludes with the actual demonstration and the results, which confirm the prediction and the principle of momentum conservation.

20:06

📚 Theoretical Calculation of Center of Mass

This paragraph shifts the focus to the concept of the center of mass in a physical system. The lecturer explains how to calculate the center of mass for a system of discrete point masses, using an example of three masses arranged in an equilateral triangle. The process involves summing the products of each mass and its position vector, and then dividing by the total mass to find the position vector of the center of mass. The calculation is broken down into x and y components to find the exact location of the center of mass. The result shows that the center of mass does not necessarily lie at the geometric center of the system, but rather is influenced by the distribution of mass.

25:06

🎾 Uniform Motion of the Center of Mass

The script discusses the predictable motion of an object's center of mass, especially in the absence of external forces. It emphasizes that while the object itself may tumble or rotate, the center of mass will maintain a uniform motion, following a parabolic trajectory when thrown, similar to a tennis ball. The lecturer demonstrates this concept using a squash racquet and a ball, showing that despite the complex motion of the racquet, its center of mass will follow a perfect parabola. This predictable behavior of the center of mass is highlighted as a key difference between the motion of the center of mass and the motion of the object as a whole.

Mindmap

Keywords

💡Momentum

Momentum is a fundamental concept in physics defined as the product of an object's mass and its velocity, resulting in a vector quantity. It is central to the video's theme as it illustrates the principle of conservation of momentum in various scenarios. The script explains that momentum is conserved during interactions, such as collisions, provided there are no external forces acting on the system, which is a key principle in physics.

💡Force

In the context of the video, force is presented as an interaction that can change an object's momentum. It is defined by the equation F = dp/dt, where F is the force, d is the change in, and p is the momentum over time (dt). The video emphasizes that a force acting on a particle will result in a change in its momentum, which is a direct consequence of Newton's second law of motion.

💡Conservation of Momentum

The conservation of momentum is a principle stating that the total momentum of a closed system remains constant if no external forces are acting on it. This concept is a core theme in the video, demonstrated through various examples including collisions and explosions. The script explains that even though individual particles' momenta may change, the total momentum of the system is conserved.

💡Internal and External Forces

The video distinguishes between internal and external forces. Internal forces are interactions between particles within a system, such as gravitational or electrical interactions, which do not affect the total momentum of the system. In contrast, external forces are those applied to the system from the outside, which can change the system's total momentum. The script uses this distinction to explain the conditions under which momentum is conserved.

💡Collision

A collision is an event in which two or more bodies exert forces on each other, often resulting in a transfer of momentum and energy. The video script discusses different types of collisions, such as completely inelastic collisions where objects stick together after the collision, and explosions where internal forces result in an increase in kinetic energy while conserving momentum.

💡Kinetic Energy

Kinetic energy is the energy that an object possesses due to its motion, defined as one-half the product of the object's mass and the square of its velocity (1/2mv^2). The video contrasts kinetic energy with momentum, showing that while momentum is always conserved in the absence of external forces, kinetic energy can change, increase, or decrease during interactions like collisions.

💡Center of Mass

The center of mass is the point at which the average position of the mass of an object is considered to be concentrated. In the video, the center of mass is discussed as a key concept related to the motion of objects, especially in the absence of external forces. The script explains that the center of mass moves uniformly and predictably, even when the object itself is tumbling or rotating.

💡Potential Energy

Potential energy is the stored energy of an object due to its position in a force field or due to its configuration. In the video, potential energy is mentioned in the context of a spring being compressed, which is then converted into kinetic energy when the spring is released, demonstrating the conservation of energy and momentum.

💡Inelastic Collision

An inelastic collision is a type of collision in which kinetic energy is not conserved because some of it is transformed into other forms of energy, such as heat or deformation. The video script uses inelastic collisions to illustrate the principle that while momentum is always conserved, kinetic energy can be lost, especially in collisions where objects stick together.

💡Vector

A vector is a quantity that has both magnitude and direction. In the context of the video, momentum is described as a vector, which means it has a size (the product of mass and velocity) and a direction associated with the velocity of the object. The script emphasizes that the vector nature of momentum is important for understanding its conservation in systems involving multiple particles.

Highlights

Introduction of the concept of momentum in physics as a vector, defined as the product of an object's mass and velocity.

Explanation of how force is related to the change in momentum, derived from Newton's second law of motion.

Illustration of the interaction between particles, including gravitational and electrical forces, and the concept of internal and external forces.

The cancellation of internal forces when considering the total momentum of a system, leading to the conservation of momentum.

The condition for the conservation of momentum: the total external force on the system must be zero.

Example of a simple one-dimensional collision demonstrating the conservation of momentum.

Difference between momentum and kinetic energy, with kinetic energy potentially decreasing or being destroyed in collisions.

Experiment showing the conservation of momentum in a collision where kinetic energy is not conserved.

Discussion on the effects of different collision types on kinetic energy, including perfectly inelastic collisions.

Experiment demonstrating the conservation of momentum with an explosion, where kinetic energy increases.

Introduction of the center of mass concept and its definition in relation to the distribution of mass in an object.

Derivation of the center of mass position for a simple system of three point masses.

Explanation of how the center of mass moves uniformly in the absence of external forces, contrasting with the complex motion of the object itself.

Demonstration of the uniform motion of the center of mass using an air track with two oscillating cars.

Visual experiment showing the center of mass motion in darkness, highlighting its constant velocity.

Final demonstration comparing the parabola of a tennis ball with the center of mass motion of a squash racquet.

Transcripts

Browse More Related Video

AP Physics 1 Momentum Review

Collisions: Crash Course Physics #10

Conservation of Linear Momentum

AP Physics 1 review of Momentum and Impulse | Physics | Khan Academy

Impulse and Momentum Conservation - Inelastic & Elastic Collisions

Momentum | Forces & Motion | Physics | FuseSchool

Related Tags

Momentum Physics Conservation Laws Vector Quantities Kinetic Energy Collision Dynamics Explosive Reactions Educational Content Physics Lecture Concept Explanation Demonstration Video