Simplifying Complex Numbers

The Organic Chemistry Tutor
29 Jan 201805:56
EducationalLearning
32 Likes 10 Comments

TLDRIn this lesson, the focus is on simplifying imaginary numbers, specifically powers of i. The instructor explains the fundamental values of i, including i, i squared, i cubed, and i to the fourth. Examples such as i to the seventh, 21st, 42nd, and 189th powers are simplified by breaking them down into combinations of these fundamental values. The process involves recognizing multiples of 4 and using basic arithmetic to simplify complex expressions involving i. The lesson ends with a practical exercise involving 3i raised to the 8th power minus 4i to the 13th power, demonstrating step-by-step simplification techniques.

Takeaways
  • 🧙‍♂️ The imaginary unit 'i' is defined as the square root of -1.
  • 🔢 'i' squared (i^2) equals -1.
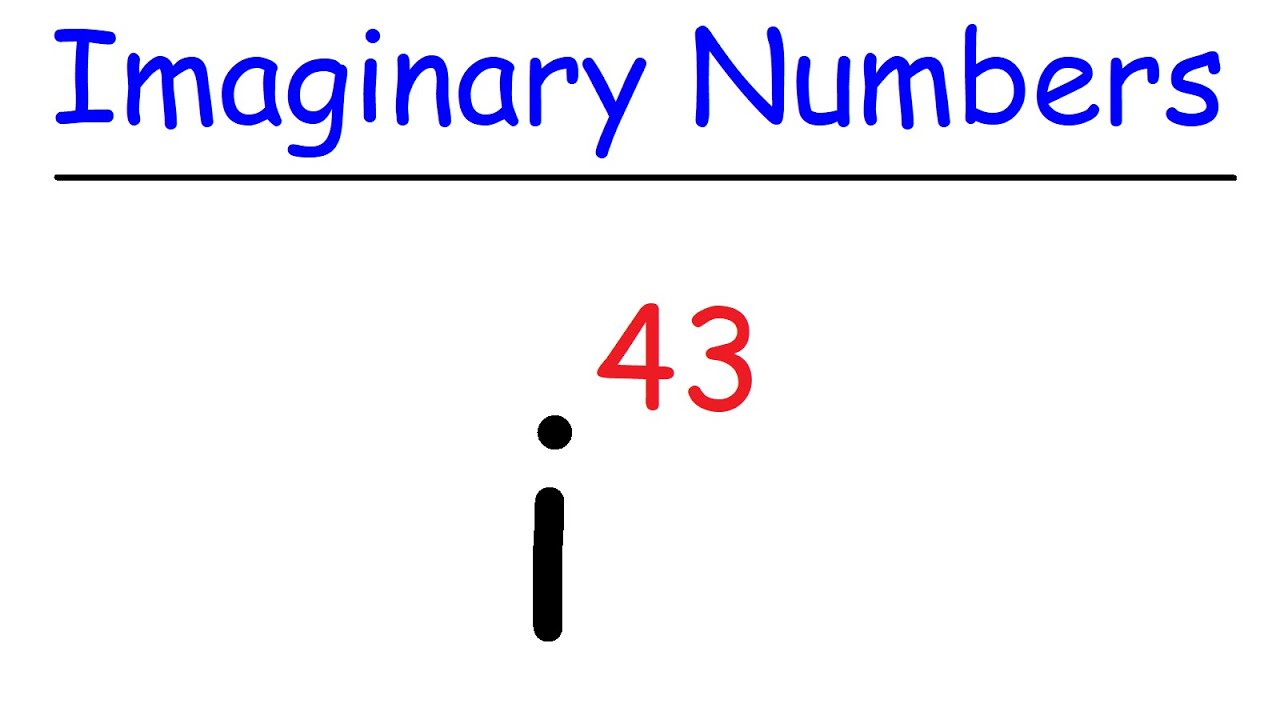
  • 👆 'i' cubed (i^3) is i^2 multiplied by i, which results in -i.
  • 📚 'i' to the fourth power (i^4) is i^2 times i^2, and since i^2 is -1, i^4 equals 1.
  • 🔄 To simplify higher powers of 'i', use the pattern that repeats every four powers: i^1=i, i^2=-1, i^3=-i, i^4=1.
  • 📉 Simplifying i^7 involves breaking it down to i^4 times i^3, knowing i^4 is 1 and i^3 is -i, thus i^7 simplifies to -i.
  • 📈 For i^21, separate it into i^20 and i^1, where i^20 is (i^4)^5 which equals 1, and i^1 is i, resulting in the answer i.
  • 📊 To simplify i^42, decompose it into i^40 and i^2, with i^40 being (i^4)^10 equaling 1, and i^2 being -1, leading to the answer -1.
  • 🧩 For numbers like i^189, divide by 4 to find the closest multiple (188) and the remainder (1), then simplify accordingly.
  • 📘 When simplifying expressions with 'i' raised to a power in a complex number like 3i^8 - 4i^13, break down the powers of i and simplify the expression step by step.
  • 🔑 The final expression 3i^8 - 4i^13 simplifies to 3(1) - 4(-1)i, which equals 3 + 4i.
Q & A

  • What is the value of i to the power of 7?

    -i to the 7th power is simplified by recognizing that i^4 * i^3 equals i^7. Since i^4 is 1 and i^3 is -i, i^7 simplifies to -i.

  • What is the significance of the number 4 when simplifying powers of i?

    -The number 4 is significant because i to the power of 4 equals 1. This is due to the cyclical nature of powers of i, where i^1 = i, i^2 = -1, i^3 = -i, and i^4 = 1, and the cycle repeats every four powers.

  • How do you simplify i to the 21st power?

    -You simplify i to the 21st power by breaking it down into i^20 * i^1. Since i^20 is (i^4)^5 and i^4 is 1, (1)^5 is still 1, so i^21 simplifies to 1 * i, which is i.

  • What is the highest multiple of 4 just under 42 when simplifying i to the 42nd power?

    -The highest multiple of 4 just under 42 is 40. This is because 40 is divisible by 4 and 40 + 2 equals 42.

  • How do you determine the two numbers to separate a given power of i into?

    -To determine the two numbers, divide the given power by 4. The whole number part of the result is the first number, and the remainder when divided by 4 is the second number.

  • What is the result of i to the 40th power?

    -i to the 40th power is (i^4)^10, which simplifies to 1^10, since i^4 is 1. Therefore, i^40 equals 1.

  • How do you simplify i to the 189th power?

    -Divide 189 by 4 to get 47.25. The whole number part, 47, multiplied by 4 gives 188, and the decimal part, 0.25, multiplied by 4 gives the remainder of 1. So, i^189 simplifies to (i^4)^47 * i^1, which is 1^47 * i, resulting in i.

  • What is the expression for i to the 8th power in terms of i to the 4th power?

    -i to the 8th power can be expressed as (i^4)^2 because 8 is a multiple of 4 (8 = 4 * 2), and since i^4 is 1, (1)^2 is still 1.

  • How do you simplify the expression 3i to the 8th power minus 4i to the 13th power?

    -3i^8 can be written as 3 * (i^4)^2, which simplifies to 3 * 1^2 = 3. For i^13, it can be broken into i^12 * i^1, where i^12 is (i^4)^3, which is 1^3 = 1, and i^1 is just i. So, 4i^13 simplifies to 4i. The final expression is 3 - 4i.

  • What is the final simplified form of the expression 3i to the 8th power minus 4i to the 13th power?

    -The final simplified form is 3 - 4i, as explained in the previous answer.

Outlines
00:00
🧙‍♂️ Simplifying Higher Powers of Imaginary Numbers

This paragraph introduces the concept of simplifying higher powers of imaginary numbers, specifically focusing on 'i', where 'i' is defined as the square root of -1. It explains the powers of 'i' up to the fourth power, establishing that 'i' squared equals -1, 'i' cubed equals -i, and 'i' to the fourth equals 1. The lesson then demonstrates how to simplify 'i' to the seventh power by breaking it down into 'i' to the fourth times 'i' to the third, resulting in -i. The method is further applied to 'i' to the 21st and 42nd powers, showing how to decompose these numbers into multiples of four and their remainders to simplify the expressions. The paragraph concludes with a step-by-step guide on how to simplify 'i' to the 189th power, emphasizing the importance of recognizing multiples of four and their impact on simplifying imaginary numbers.

05:01
📚 Advanced Simplification of Imaginary Numbers

Building upon the foundation laid in the previous paragraph, this section delves into more complex simplifications of imaginary numbers. It begins by simplifying '3i' raised to the 8th power, showing that since 8 is a multiple of 4, it can be expressed as 'i' to the fourth squared, resulting in 1. The process continues with simplifying '4i' to the 13th power, breaking down the exponent into 12 (a multiple of 4) and 1. The explanation details that 'i' to the fourth is 1, and 'i' to the twelfth (which is 'i' to the fourth times three) equals 3, leading to the final answer of 3 minus 4 times 'i'. The paragraph also touches on the simplification of 'i' cubed, reinforcing the concept that 'i' cubed equals -i, and concludes with the final simplified expression.

Mindmap
Keywords
💡Imaginary Numbers
Imaginary numbers are a mathematical concept that extends the real number system to include numbers that, when squared, give a negative result. The most well-known imaginary number is 'i', which is defined as the square root of -1. In the video, imaginary numbers are the central theme, as the script focuses on simplifying powers of 'i', demonstrating how to handle different exponents of this imaginary unit.
💡i to the seventh power
This term refers to raising the imaginary unit 'i' to the seventh power, which is a specific calculation within the context of imaginary numbers. The script explains how to simplify 'i' to the seventh power by breaking it down into 'i' to the fourth power times 'i' to the third power, leveraging known values of 'i' raised to the second, third, and fourth powers.
💡Simplification
Simplification in mathematics refers to the process of making a complex expression or equation more straightforward or easier to understand. In the context of the video, simplification is the method used to reduce the powers of 'i' to more manageable forms, such as 'i' squared being -1, 'i' cubed being -i, and 'i' to the fourth being 1.
💡Exponents
Exponents are used to denote the number of times a base number is multiplied by itself. In the script, exponents are crucial for understanding how to simplify powers of 'i'. For example, 'i' to the third power is 'i' squared (which is -1) times 'i', resulting in -i.
💡i squared
The term 'i squared' refers to the imaginary unit 'i' multiplied by itself. According to the script, 'i' squared equals -1, which is a fundamental property used to simplify higher powers of 'i'.
💡i cubed
'i cubed' is the result of multiplying 'i' by itself three times. The script explains that 'i' cubed equals 'i' squared (which is -1) times 'i', simplifying to -i. This is a key step in simplifying 'i' to higher powers.
💡i to the fourth
'i to the fourth' is another fundamental power of 'i' that equals 1, as explained in the script. This is because 'i' squared is -1, and -1 times -1 equals 1. This property is used repeatedly in simplifying higher powers of 'i'.
💡Multiples of Four
In the context of simplifying powers of 'i', multiples of four are important because 'i' to the fourth power equals 1. The script uses multiples of four to break down exponents into more manageable parts, such as 'i' to the twentieth being 'i' to the fourth raised to the fifth power.
💡Raising to a Power
Raising to a power means multiplying the base number by itself the number of times indicated by the exponent. In the script, this concept is used to simplify expressions like 'i' to the twentieth by expressing it as 'i' to the fourth raised to the fifth power.
💡Decimal Part
The decimal part of a number refers to the fractional component when the number is expressed as a fraction. In the script, the decimal part is used to determine the remainder when dividing the exponent by four, which helps in breaking down the exponent into a product of 'i' to the fourth and a simpler power of 'i'.
💡Complex Numbers
While not explicitly mentioned in the script, complex numbers are an extension of the concept of imaginary numbers. A complex number is a number of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit. The script's focus on powers of 'i' ties into the broader topic of complex numbers, where such powers are used to simplify and understand expressions involving complex numbers.
Highlights

Introduction to simplifying imaginary numbers.

Explanation of the value of i (the square root of negative one).

Understanding i squared as negative one.

Simplifying i cubed as negative i.

Simplifying i to the fourth power as one.

Importance of knowing i squared, i cubed, and i to the fourth.

Step-by-step simplification of i to the seventh power.

Explanation of the method to simplify i to the 21st power.

Using multiples of four to simplify higher powers of i.

Detailed process for simplifying i to the 42nd power.

Using division by four to decompose powers of i.

Simplifying i to the 189th power using the highest multiple of four.

Decomposing 3i raised to the 8th power using i to the fourth.

Simplifying complex expressions like 3i^8 - 4i^13.

Importance of breaking down higher powers into known values of i.

Transcripts

Browse More Related Video

Multiplying Complex Numbers

Summation Formulas and Sigma Notation - Calculus

Ch. 1.6 Complex Numbers

Imaginary Numbers - Basic Introduction

Complex Numbers - Basic Operations

Dividing Complex Numbers

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Imaginary NumbersMathematicsEducationalSimplificationi PowersAlgebraComplex NumbersRoots of UnityMath Tutoriali^4i^3