How To Find The Inverse of a Function

The Organic Chemistry Tutor
8 Sept 201711:36
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video offers a step-by-step guide on finding the inverse of a function. It begins with a simple linear function and progresses to more complex examples, including cubic and square root functions. The process involves replacing 'f(x)' with 'y', swapping 'x' and 'y', and isolating 'y' through algebraic manipulation. Techniques such as taking square roots, cubing both sides, and cross-multiplication are demonstrated to solve for the inverse function. The video concludes with a challenging example involving a rational function, reinforcing the method of cross-multiplication and factoring to isolate the variable.

Takeaways
  • 📚 The video explains the process of finding the inverse of a function step by step.
  • 🔄 The first step is to replace 'f(x)' with 'y' to set up the equation for finding the inverse.
  • 🔄 Next, switch 'x' and 'y' in the equation to start isolating 'y'.
  • 🔢 For linear functions like 'f(x) = 2x - 7', isolate 'y' by adding 7 to both sides and then dividing by 2.
  • 📈 For cubic functions like 'f(x) = x^3 + 8', isolate 'y' by taking the cube root of both sides.
  • 📊 For square root functions like '√(x + 2) - 5', isolate 'y' by squaring both sides of the equation.
  • 🔢 When dealing with a cube root function, such as '∛(x + 4) - 2', take the cube of both sides to remove the cube root.
  • 🔍 For rational functions like 'f(x) = (3x - 7) / (4x + 3)', cross-multiply and isolate 'y' by moving terms involving 'y' to one side.
  • 📚 The process involves algebraic manipulation to isolate 'y' and then swapping 'x' and 'y' to get the inverse function.
  • 📝 The final answer for the inverse function is written in terms of 'x', representing the input variable.
  • 📉 The video also shows alternative ways to express the inverse function, such as leaving the equation in its squared form or expanded form.
Q & A

  • What is the first step in finding the inverse of a function?

    -The first step in finding the inverse of a function is to replace f(x) with y, since y and f(x) represent the same thing.

  • How do you proceed after replacing f(x) with y in the process of finding an inverse function?

    -After replacing f(x) with y, the next step is to switch x with y in the equation to start solving for the inverse.

  • What is the purpose of isolating the variable y in the equation when finding the inverse function?

    -Isolating the variable y is necessary to solve for y and get it by itself on one side of the equation, which will give you the inverse function.

  • Can you provide an example of a simple function and its inverse as described in the script?

    -An example from the script is the function f(x) = 2x - 7. The inverse function is found by replacing f(x) with y, switching x with y, and isolating y to get the inverse function y = (x + 7) / 2.

  • What mathematical operation is used to solve for y in the example where f(x) = x^3 + 8?

    -In the example where f(x) = x^3 + 8, the mathematical operation used to solve for y is taking the cube root of both sides of the equation.

  • How do you deal with a square root in the process of finding an inverse function, as shown in the script?

    -To deal with a square root when finding an inverse function, you can square both sides of the equation to eliminate the square root, as demonstrated in the script with the function f(x) = sqrt(x + 2) - 5.

  • What is the inverse function of f(x) = sqrt(x + 2) - 5 according to the script?

    -The inverse function of f(x) = sqrt(x + 2) - 5 is y = x^2 + 10x + 23, after simplifying the expression obtained by squaring both sides of the equation.

  • Can the inverse function be expressed in a different but equivalent form, as shown in the script?

    -Yes, the inverse function can be expressed in a different but equivalent form. For example, the inverse function of f(x) = sqrt(x + 2) - 5 can also be written as y = (x + 5)^2 - 2 before simplifying.

  • How do you handle a cube root function when finding its inverse, as illustrated in the script?

    -To handle a cube root function when finding its inverse, you can take the cube of both sides of the equation to eliminate the cube root, as shown in the script with the function f(x) = cuberoot(x + 4) - 2.

  • What is the inverse function of a rational function like f(x) = (3x - 7) / (4x + 3), according to the script?

    -The inverse function of a rational function like f(x) = (3x - 7) / (4x + 3) is found by cross-multiplying, isolating y, and simplifying to get y = (3x + 7) / (3 - 4x).

  • Why is it important to move all terms with the variable y to one side of the equation when finding the inverse function of a rational function?

    -It is important to move all terms with the variable y to one side to factor out y and isolate it, which allows you to solve for y and find the inverse function, as demonstrated with the function f(x) = (3x - 7) / (4x + 3).

Outlines
00:00
📚 Finding the Inverse of a Linear Function

This paragraph introduces the concept of finding the inverse of a function with a specific example. The function f(x) = 2x - 7 is used to demonstrate the process step-by-step. The first step involves replacing f(x) with y, then switching x and y to get x = 2y - 7. The next step is to isolate y by adding 7 to both sides, resulting in x + 7 = 2y, and then dividing by 2 to get y = (x + 7) / 2. The final expression y = (x + 7) / 2 is presented as the inverse function. The paragraph also briefly introduces the process for finding the inverse of a function f(x) = x^3 + 8, where the steps include taking the cube root of both sides to isolate y.

05:02
🔍 Inverse Functions of Exponential and Radical Equations

This paragraph continues the discussion on inverse functions, focusing on more complex examples involving exponential and radical expressions. The first example is the inverse of f(x) = √(x + 2) - 5, which involves switching x and y, then isolating y by adding 5 to both sides and squaring both sides to eliminate the square root. The resulting equation is simplified to y = x^2 + 10x + 23. An alternative method is presented, where the inverse function can be written as y = (x + 5)^2 - 2 before simplifying. The second example involves a cube root function, f(x) = ∛(x + 4) - 2, where the cube is eliminated by cubing both sides, leading to the inverse function y = x^3 + 2 - 4. The paragraph concludes with a more complex rational function example, f(x) = (3x - 7) / (4x + 3), which requires cross-multiplication and rearranging terms to isolate y, resulting in the inverse function y = (3x + 7) / (3 - 4x).

10:04
📘 Final Thoughts on Inverse Function Calculation

The final paragraph wraps up the discussion on finding inverse functions. It emphasizes the methodical approach of switching f(x) with y, swapping x and y, and then isolating the y variable through algebraic manipulation. The paragraph also highlights the importance of understanding the algebraic steps for different types of functions, such as linear, exponential, radical, and rational. It provides a comprehensive overview of the process, from initial substitution to the final isolation of the variable, and encourages practice with various function types to master the skill of finding inverse functions.

Mindmap
Keywords
💡Inverse of a function
The inverse of a function is a mathematical concept where you reverse the roles of the input and output of a given function. In the context of the video, it's the process of finding a new function that, when applied to the original function, returns the original input. This is crucial for understanding how to reverse the effects of a mathematical transformation. For example, the video demonstrates finding the inverse of 'f(x) = 2x - 7' by replacing 'f(x)' with 'y' and then solving for 'y' in terms of 'x'.
💡Replace f(x) with y
This step is part of the process to find the inverse of a function. It involves substituting the function notation 'f(x)' with the variable 'y' to simplify the algebraic manipulation that follows. In the video, this is the initial step taken to begin the process of finding an inverse function, as seen when transitioning from 'f(x) = 2x - 7' to 'y = 2x - 7'.
💡Switch x with y
This concept refers to the step in which you interchange the variables 'x' and 'y' in the equation derived from the original function. This is done to set up the equation for solving 'y' in terms of 'x', which is necessary to find the inverse function. The video script illustrates this with 'x = 2y - 7' after initially setting 'y = 2x - 7'.
💡Isolate the variable
Isolating the variable means solving the equation to have 'y' alone on one side, which is a key step in determining the inverse function. In the video, this is done through algebraic manipulation, such as adding or subtracting terms and dividing by coefficients, as shown when moving from 'x + 7 = 2y' to 'y = (x + 7) / 2'.
💡Cube root
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. In the video, the cube root is used in the context of inverse functions to undo a cubic transformation, such as finding the inverse of 'f(x) = x^3 + 8' by taking the cube root of both sides to solve for 'y'.
💡Square root
The square root of a number is a value that, when squared (multiplied by itself), results in the original number. In the video, the process of finding the inverse of a function involving a square root, such as 'f(x) = sqrt(x + 2) - 5', involves squaring both sides of the equation to eliminate the square root and solve for 'y'.
💡Foil method
Foil is a method used for multiplying two binomials. It stands for 'First, Outer, Inner, Last', which refers to the steps of multiplying each term in one binomial by each term in the other. In the script, this method is used when expanding '(x + 5)^2' to find the inverse function of a square root function.
💡Combine like terms
Combining like terms is the process of adding or subtracting terms in an equation that have the same variable raised to the same power. This simplification step is used in the video when simplifying expressions like 'x^2 + 10x + 25' after expanding '(x + 5)^2'.
💡Cube of both sides
Raising both sides of an equation to the third power is a technique used to eliminate cube roots, as cube roots and cubing are inverse operations. The video demonstrates this when finding the inverse of a function involving a cube root, such as 'f(x) = (x + 4)^(1/3) - 2', by cubing both sides to solve for 'y'.
💡Cross multiply
Cross multiplication is a method used to solve proportions or equations involving fractions by multiplying each term by the denominator of the other term. In the video, this technique is suggested to isolate the variable 'y' when dealing with a rational function, such as 'f(x) = (3x - 7) / (4x + 3)'.
💡Factor out
Factoring out is the process of taking a common factor from a group of terms in a polynomial or an equation. In the context of the video, factoring out 'y' from terms like '3y - 4yx' simplifies the equation and helps isolate 'y', as shown in the process of finding the inverse function of 'f(x) = (3x - 7) / (4x + 3)'.
Highlights

Introduction to finding the inverse of a function.

Explanation of replacing f(x) with y to start the process.

Step-by-step guide to switch x and y variables.

Isolating y by manipulating the equation.

Example of finding inverse for f(x) = 2x - 7.

Final expression for the inverse function of the first example.

Approach to finding inverse for f(x) = x^3 + 8.

Method to solve for y by taking the cube root.

Inverse function for the cubic function example.

Process for finding inverse of f(x) = sqrt(x + 2) - 5.

Technique of squaring both sides to remove the square root.

Final expression for the inverse function of the square root example.

Alternative expression for the inverse function using subtraction.

Introduction to inverse function of a cube root function.

Method to eliminate the cube root by cubing both sides.

Final expression for the inverse function of the cube root example.

Complex example with f(x) = (3x - 7) / (4x + 3).

Strategy for isolating y in the complex rational function.

Final expression for the inverse function of the complex example.

Transcripts

Browse More Related Video

Inverse Functions - Domain & range- With Fractions, Square Roots, & Graphs

Evaluating Functions - Basic Introduction | Algebra

Function inverses example 3 | Functions and their graphs | Algebra II | Khan Academy

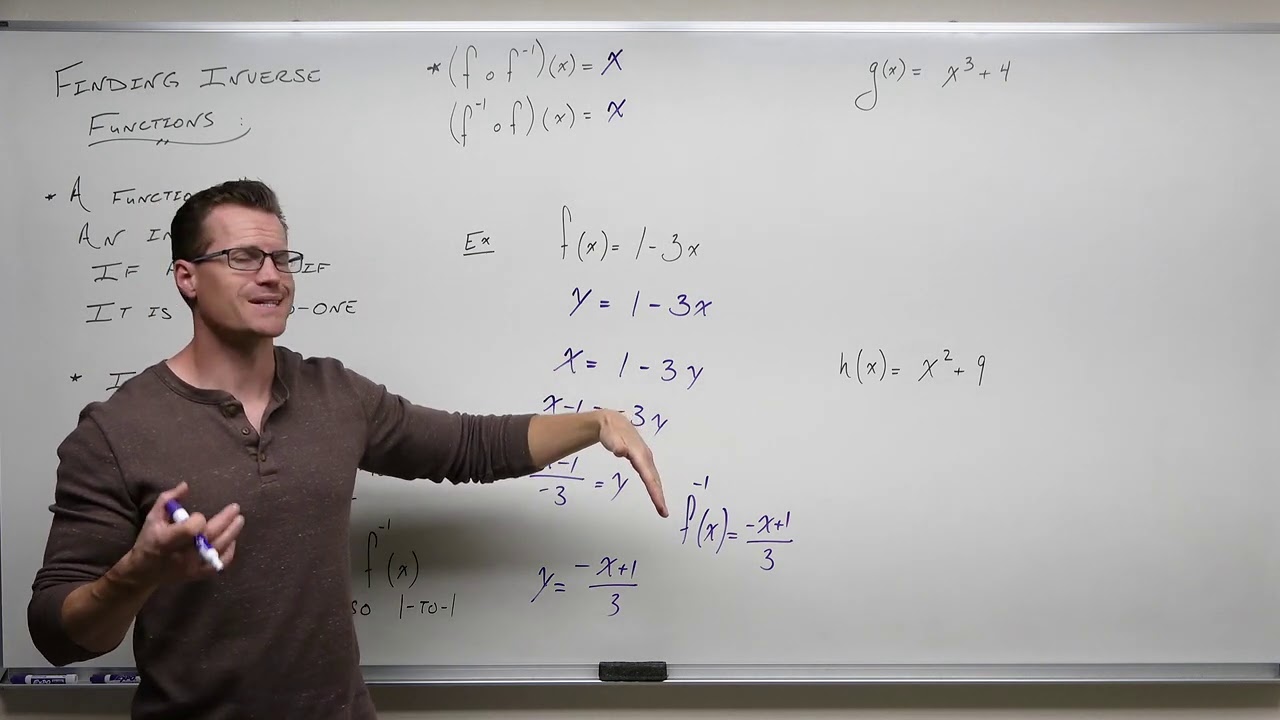
Finding Inverse Functions (Precalculus - College Algebra 51)

Function inverses example 2 | Functions and their graphs | Algebra II | Khan Academy

Inverse Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Inverse FunctionsMathematics TutorialFunction TransformationAlgebraic TechniquesEducational ContentMath Problem SolvingFunction IsolationEquation ManipulationMathematical ExamplesLearning Resource