Lecture 19: Mountain Slopes and Tangent Planes
TLDRThis calculus lecture explores functions of several variables, focusing on how a single value can depend on multiple independently varying quantities, exemplified by the volume of a box determined by its width, length, and height. The instructor delves into partial derivatives, directional derivatives, and tangent planes, illustrating these concepts with examples like the area of a rectangle and altitude on a mountainous terrain. The lecture also discusses optimization, identifying maximum and minimum points on a graph by setting partial derivatives to zero, using the function f(x, y) = sin(x)sin(y) as a case study. The concepts are presented as tools to analyze real-world situations involving multiple variables, with the promise of extending the ideas of the integral to three-dimensional objects in the next lecture.
Takeaways
- 📚 The lecture introduces the concept of functions of several variables, where one value is dependent on multiple independently varying quantities, such as the volume of a box depending on its width, length, and height.
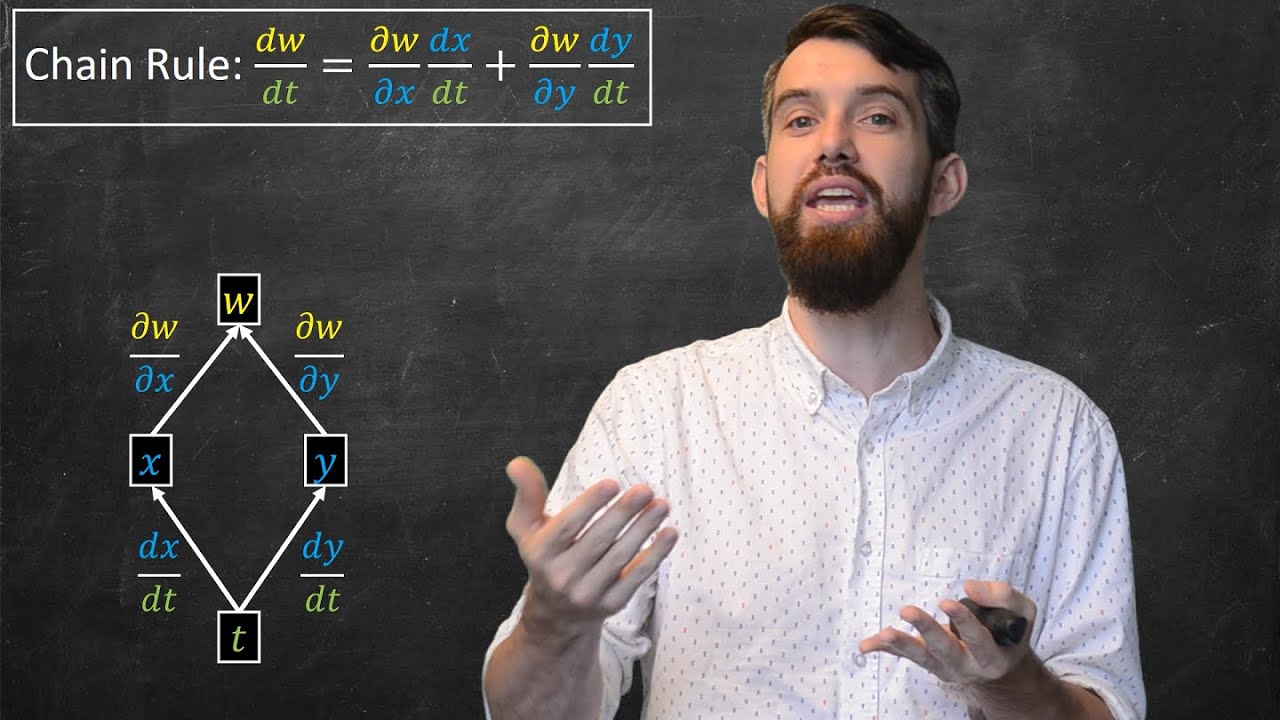
- 🧭 The idea of partial derivatives is explored, which is a generalization of the derivative concept to functions of multiple variables, allowing us to examine how a function changes with respect to one variable while holding others constant.
- 📈 The script explains how to calculate partial derivatives with respect to each variable, using the area of a rectangle as an example to illustrate how the area changes with respect to changes in length and width.
- 🗺️ The concept of directional derivatives is introduced, which extends the idea of derivatives to different directions, akin to determining whether you are going uphill or downhill on a terrain when moving in various directions.
- 📊 The lecture discusses tangent planes as an analogy to the tangent lines in single-variable calculus, showing that at any given point on a surface, there is a plane that closely approximates the surface locally, with its orientation determined by the partial derivatives.
- 🔍 The script uses the function f(x, y) = -x^2 + y^2 to visually demonstrate the concept of partial derivatives and tangent planes, with the graph resembling a cone pointing upwards from the origin.
- 📘 The function f(x, y) = sin(x) * sin(y) is used as an example to illustrate how to find critical points where both partial derivatives are zero, which could indicate local maxima or minima.
- 📚 The importance of understanding the geometric interpretation of partial derivatives is emphasized, as they reveal the slope of the function in the direction of each variable, akin to the steepness of a terrain.
- 🔑 The script highlights that many real-world situations involve multiple variables, such as weight being dependent on diet, genetics, and exercise, and how calculus provides strategies to analyze these complex relationships.
- 🚀 The lecture concludes with a preview of the next topic, which will be the extension of integral calculus to deal with three-dimensional objects and situations.
Q & A
What is the main topic discussed in this calculus lecture?
-The main topic discussed in this calculus lecture is functions of several variables, specifically how to adapt the concepts of calculus, such as derivatives, to situations where a single value is dependent on two or more independently varying quantities.
Why is the volume of a box a good example to illustrate a function of several variables?
-The volume of a box is a good example because it clearly demonstrates how three varying quantities (width, length, and height) can determine one value (volume), which is the essence of a function of several variables.
What is a directional derivative and why is it important in the context of functions of several variables?
-A directional derivative is a derivative that measures how fast a function changes in a particular direction. It is important in the context of functions of several variables because it allows us to investigate the rate of change of a function in various directions from a given point, which is not limited to just the x or y direction as in single-variable functions.
How does the concept of a tangent plane relate to functions of two variables?
-The concept of a tangent plane relates to functions of two variables by providing a way to visualize and understand the local behavior of the function near a specific point. At a given point, the tangent plane is the flat plane that best approximates the surface of the function, and it is oriented according to the partial derivatives at that point.
What is the relationship between the partial derivatives of a function and the rates of change of the function's value?
-The partial derivatives of a function with respect to its variables indicate the rate at which the function's value changes when only one variable is varied at a time, holding the others constant. This provides insight into how sensitive the function's value is to changes in each variable independently.
Can you explain how the area of a rectangle is used as an example to discuss partial derivatives in the script?
-The area of a rectangle, given by the product of its length (L) and width (W), is used to illustrate the concept of partial derivatives. By asking how fast the area changes with respect to a change in length or width independently, the script demonstrates how to compute partial derivatives and what they represent in terms of the rate of change of the area.
What is the significance of the point (1,1) in the context of the function f(x, y) = -x^2 + y^2?
-The point (1,1) is significant because at this point, the partial derivatives with respect to both x and y are non-zero and have the same magnitude but opposite signs, indicating that moving in the x-direction results in a downward slope, and moving in the y-direction results in an upward slope, reflecting the geometric features of the graph.
How does the script use the function f(x, y) = sin(x) * sin(y) to discuss critical points in functions of two variables?
-The script uses the function f(x, y) = sin(x) * sin(y) to demonstrate how to find critical points by setting the partial derivatives with respect to x and y to zero. The point (pi/2, pi/2) is identified as a critical point because both partial derivatives are zero at this location, indicating a potential maximum or minimum.
What is the graphical representation of the function f(x, y) = -x^2 + y^2, and how does it relate to the concept of tangent planes?
-The graphical representation of the function f(x, y) = -x^2 + y^2 is a cone-shaped surface with a peak at the origin. The concept of tangent planes is related to this function as the script explains that at any point on the surface, a tangent plane can be imagined that is flat and oriented according to the slopes given by the partial derivatives at that point.
How does the script connect the idea of optimization in single-variable calculus to functions of two variables?
-The script connects the idea of optimization by stating that for functions of two variables, maximum or minimum points occur where both partial derivatives with respect to each variable are zero, similar to how a single-variable function has a maximum or minimum where its derivative is zero.
Outlines
🚗 Introduction to Functions of Several Variables
This paragraph introduces the concept of functions of several variables, where a single value is determined by multiple independently varying quantities. The lecturer uses the example of a car's position, determined by its x and y coordinates over time, to transition into more complex scenarios where quantities like the volume of a box are dependent on its width, length, and height. The goal is to apply the concepts of calculus, specifically derivatives, to these multi-variable functions and understand how changes in one variable affect the overall outcome.
📏 Exploring Directional Derivatives and Tangent Planes
The lecturer delves into the concept of directional derivatives, which are derivatives in various directions on a multi-variable function, using the analogy of navigating mountainous terrain. The idea of a tangent plane is introduced as a two-dimensional surface that locally approximates a multi-variable function at a given point, similar to how a tangent line approximates a function of a single variable. The paragraph discusses how these concepts can be used to understand the rate of change of a function in different directions and how the terrain behaves locally around a point.
📐 Partial Derivatives and the Area of a Rectangle
This section focuses on partial derivatives, starting with a simple example of the area of a rectangle, which is a function of its length and width. The lecturer explains how to calculate the rate of change of the area with respect to changes in the length and width independently, which are the partial derivatives. The example illustrates how to compute these derivatives at a specific point and how to interpret the results, showing that the area increases at a rate equal to the other dimension when one dimension is varied.
📈 Directional Derivatives in Diagonal Directions
Building on the concept of partial derivatives, the lecturer explores how to calculate the rate of change of the area of a rectangle when both length and width are varied simultaneously in a diagonal direction. This introduces the concept of directional derivatives, which measure the rate of change of a function in a specific direction. The paragraph provides a detailed calculation using the Pythagorean theorem to find the rate of change of the area in the diagonal direction, resulting in a rate of change of seven halves per unit change in the diagonal direction.
📊 Interpreting Partial Derivatives Geometrically
The paragraph discusses the geometric interpretation of partial derivatives using the function f(x, y) = -x^2 + y^2, which represents a three-dimensional graph resembling a cone. The lecturer explains how to compute the partial derivatives with respect to x and y, which indicate the slope of the function in the x and y directions, respectively. These derivatives provide insight into the steepness and direction of the slope at any point on the graph, helping to visualize the terrain's features.
🔍 Tangent Planes and Optimization
The lecturer introduces the concept of tangent planes, which are flat planes that touch a three-dimensional surface at a single point, providing a local linear approximation of the surface. The paragraph discusses how tangent planes can be used to find maximum or minimum points on a surface, where both partial derivatives are zero, indicating a horizontal tangent plane. The example of the function f(x, y) = sin(x) * sin(y) is used to illustrate how to find such points by setting the partial derivatives to zero and analyzing the graph.
🌐 Applications of Multi-Variable Functions in Real-World Scenarios
In the final paragraph, the lecturer connects the concepts discussed to real-world applications, such as how multiple variables like diet, genetics, and exercise affect our weight, or how income and spending affect our bank balances. The paragraph emphasizes the importance of analyzing how changes in each variable independently can provide insight into their combined effects. The lecturer also previews the next lecture, which will explore how integral calculus can be extended to three-dimensional objects.
Mindmap
Keywords
💡Function of several variables
💡Partial derivatives
💡Directional derivatives
💡Tangent plane
💡Terrain
💡Volume
💡Altitude
💡Optimization
💡Derivatives
💡Graph
Highlights
Introduction to functions of several variables, where one value depends on multiple independently varying quantities.
Exploration of volume of a box as an example of a function of several variables, dependent on width, length, and height.
Adapting calculus concepts, specifically derivatives, to functions of several variables.
Concept of altitude on a mountainous terrain as an introduction to functions of two variables.
Discussion on the rate of change of altitude in different directions on a terrain.
Introduction of directional derivatives to determine the rate of change in various directions.
Analogous situation of a tangent plane to a terrain, compared to a tangent line to a graph.
Explanation of partial derivatives as the rate of change of a function with respect to one variable while others are constant.
Example of calculating partial derivatives for the area of a rectangle with respect to length and width.
Investigation of the rate of change of area when both length and width change simultaneously.
Visual representation of a function of two variables, f(x, y) = -x^2 + y^2, and its interpretation as a cone shape.
Computation and interpretation of partial derivatives for the function f(x, y) = -x^2 + y^2 at specific points.
Demonstration of how partial derivatives reveal geometric features of the graph, such as slopes and direction of movement.
Explanation of tangent planes as the local representation of a surface, analogous to a flat plane on a hilltop.
Procedure to find maximum or minimum points of a function of two variables using partial derivatives.
Application of the concept of optimization to functions of two variables, exemplified by the function f(x, y) = sin(x) * sin(y).
Graphical representation of the function f(x, y) = sin(x) * sin(y), illustrating maxima and minima points.
Real-world applications of functions of several variables, such as weight dependent on diet, genetics, and exercise.
Conclusion summarizing the generalization of derivatives and tangent lines to partial derivatives, directional derivatives, and tangent planes.
Anticipation of the next lecture, which will explore the extension of integral calculus to three-dimensional objects.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: