2022 AP Calculus BC Exam FRQ #2
TLDRThe video script discusses a vector parametric equations problem from the 2022 AP Calculus BC exam. It involves a particle moving along a curve in the xy-plane, with its position defined by parametric equations involving square root and natural logarithm functions. The video guides viewers through finding the slope of the tangent line to the particle's path at t=4, the speed and acceleration vector of the particle at t=4, the y-coordinate of the particle's position at t=6, and the total distance traveled by the particle from t=4 to t=6. The presenter uses a calculator to perform the necessary calculations and emphasizes the importance of starting the calculations from t=4. The problem is solved step by step, making it accessible to viewers with a basic understanding of calculus.
Takeaways
- 📐 The problem involves a particle moving along a curve in the xy-plane with parametric equations given by dx/dt and dy/dt.
- ⏱️ The particle's motion starts at time t=4, not at t=0 or t=1, which is a crucial starting point for calculations.
- 📍 At t=4, the particle's position is given as (1, 5), which is significant for subsequent calculations.
- 🔍 To find the slope of the tangent line at t=4, use the derivative dy/dx, which equals dy/dt divided by dx/dt.
- 🧮 The exact value of the slope at t=4 is calculated as the natural log of 18 divided by 17, approximately 0.701.
- 🚀 The speed of the particle at t=4 is found by taking the square root of (dx/dt)^2 + (dy/dt)^2 and is approximately 5.035.
- 📉 The acceleration vector at t=4 is determined by finding the second derivatives of x and y with respect to t and is given as (0.970, 0.444).
- 🔢 To find the y-coordinate of the particle's position at t=6, integrate dy/dt from 4 to 6 and add it to the initial y-value at t=4, resulting in 11.571.
- 🏞️ The total distance traveled by the particle from t=4 to t=6 is calculated by integrating the speed over that interval, yielding approximately 12.136.
- 💡 The problem emphasizes the connection between velocity and acceleration, and their relationship to the particle's position.
- 📝 The use of a calculator is essential for performing the complex mathematical operations involved in the problem.
Q & A
What is the problem statement from the 2022 Calc BC exam?
-The problem involves a particle moving along a curve in the xy-plane with parametric equations given by dx/dt being the square root of one plus t squared and dy/dt being the natural log of two plus t squared. The particle's position at time t=4 is given as (1, 5), and the task is to find various quantities related to the particle's motion, including the slope of the tangent line, speed, acceleration vector, y-coordinate at t=6, and the total distance traveled from t=4 to t=6.
What is the expression for the slope of the tangent line to the particle's path at t=4?
-The slope of the tangent line, denoted as dy/dx, is calculated by dy/dt divided by dx/dt and is evaluated at t=4, which results in the natural log of 18 divided by 17.
What is the approximate value of the slope of the tangent line at t=4?
-The approximate value of the slope at t=4 is 0.701.
How is the speed of the particle at time t=4 calculated?
-The speed of the particle at t=4 is found by taking the magnitude of the velocity vector, which is the square root of (dx/dt)^2 + (dy/dt)^2, and evaluating it at t=4.
What is the speed of the particle at time t=4?
-The speed of the particle at t=4 is approximately 5.035.
How is the acceleration vector of the particle at time t=4 determined?
-The acceleration vector is determined by finding the second derivatives of x and y with respect to t, denoted as d^2x/dt^2 and d^2y/dt^2, and then evaluating them at t=4.
What are the components of the acceleration vector at t=4?
-The components of the acceleration vector at t=4 are approximately 0.970 for the x-component and 0.444 for the y-component.
What is the method used to find the y-coordinate of the particle's position at time t=6?
-The y-coordinate at t=6 is found by starting from the known position at t=4 (y of 4) and adding the displacement of y, which is the integral from 4 to 6 of dy/dt dt.
What is the y-coordinate of the particle's position at time t=6?
-The y-coordinate of the particle's position at time t=6 is approximately 11.571.
How is the total distance traveled by the particle from t=4 to t=6 calculated?
-The total distance traveled is the integral from 4 to 6 of the speed, which is the magnitude of velocity, calculated as the square root of (dx/dt)^2 + (dy/dt)^2.
What is the total distance traveled by the particle from t=4 to t=6?
-The total distance traveled by the particle from t=4 to t=6 is approximately 12.136.
What is the significance of starting the particle's motion at t=4 rather than t=0 or t=1?
-Starting the particle's motion at t=4 is significant because it provides a specific initial condition for the particle's position and velocity, which is necessary for calculating subsequent quantities such as the slope of the tangent line, speed, acceleration, and the particle's position at a later time.
What is the fundamental theorem of calculus used for in this problem?
-The fundamental theorem of calculus is used to find the displacement of the particle by integrating the derivative of the particle's position (dy/dt) over the interval from t=4 to t=6.
Outlines
📚 Vector Parametric Equations Problem
The video script begins with an introduction to a vector parametric equations problem from the 2022 calculus BC exam. The problem involves a particle moving along a curve in the xy-plane with its position defined by parametric equations for x(t) and y(t). The particle's velocity components are given by dx/dt and dy/dt, with specific expressions involving square root and natural logarithm functions. The video demonstrates how to find the slope of the tangent line to the particle's path at t=4, using the derivatives of x(t) and y(t). The exact value obtained is the natural logarithm of 18 divided by 17, which is approximately 0.701. The script then proceeds to calculate the speed of the particle at t=4 by taking the square root of the sum of the squares of the derivatives dx/dt and dy/dt, resulting in a speed of approximately 5.035. The acceleration vector at t=4 is also calculated, using the second derivatives of x(t) and y(t). Lastly, the y-coordinate of the particle's position at t=6 is determined by integrating dy/dt from t=4 to t=6, starting from the known position at t=4, yielding a value of 11.571. The total distance traveled by the particle from t=4 to t=6 is then calculated by integrating the speed over the same time interval, resulting in an approximate distance of 12.136.
🎓 Conclusion and Good Luck Wish
The video script concludes with a brief summary of the problem, emphasizing its straightforward nature. The presenter expresses hope that the explanation was helpful to the viewer and wishes them good luck, indicating the end of the problem-solving segment.
Mindmap
Keywords
💡Vector Parametric Equations
💡Derivative
💡Slope of the Tangent Line
💡Speed
💡Acceleration Vector
💡Displacement
💡Fundamental Theorem of Calculus
💡Distance Traveled
💡Calculator
💡Integration
💡Magnitude of Velocity
Highlights
The problem involves a particle moving along a curve in the xy-plane with parametric equations.
The particle's position is defined by dx/dt = √(1 + t^2) and dy/dt = ln(2 + t^2) for t > 0.
At t = 4, the particle is at the point (1, 5).
The slope of the tangent line to the path at t = 4 is found using dy/dx = dy/dt / dx/dt.
The exact value of the slope at t = 4 is ln(18)/17, approximately 0.701.
The speed of the particle at t = 4 is calculated using the magnitude of velocity.
The acceleration vector at t = 4 is determined by finding the second derivatives of x and y with respect to t.
The speed at t = 4 is found to be approximately 5.035.
The acceleration vector components at t = 4 are approximately 0.970 and 0.444.
The y-coordinate of the particle's position at t = 6 is calculated using the integral of dy/dt from 4 to 6.
The y-coordinate at t = 6 is approximately 11.571 after adding the displacement to the initial y-coordinate at t = 4.
The total distance traveled by the particle from t = 4 to t = 6 is found by integrating the speed over the time interval.
The integral of the speed from t = 4 to t = 6 yields a distance of approximately 12.136.
The problem is straightforward and involves using a calculator for precise calculations.
The transcript provides a step-by-step approach to solving the vector parametric equations problem.
The use of the fundamental theorem of calculus is emphasized for finding displacement and distance traveled.
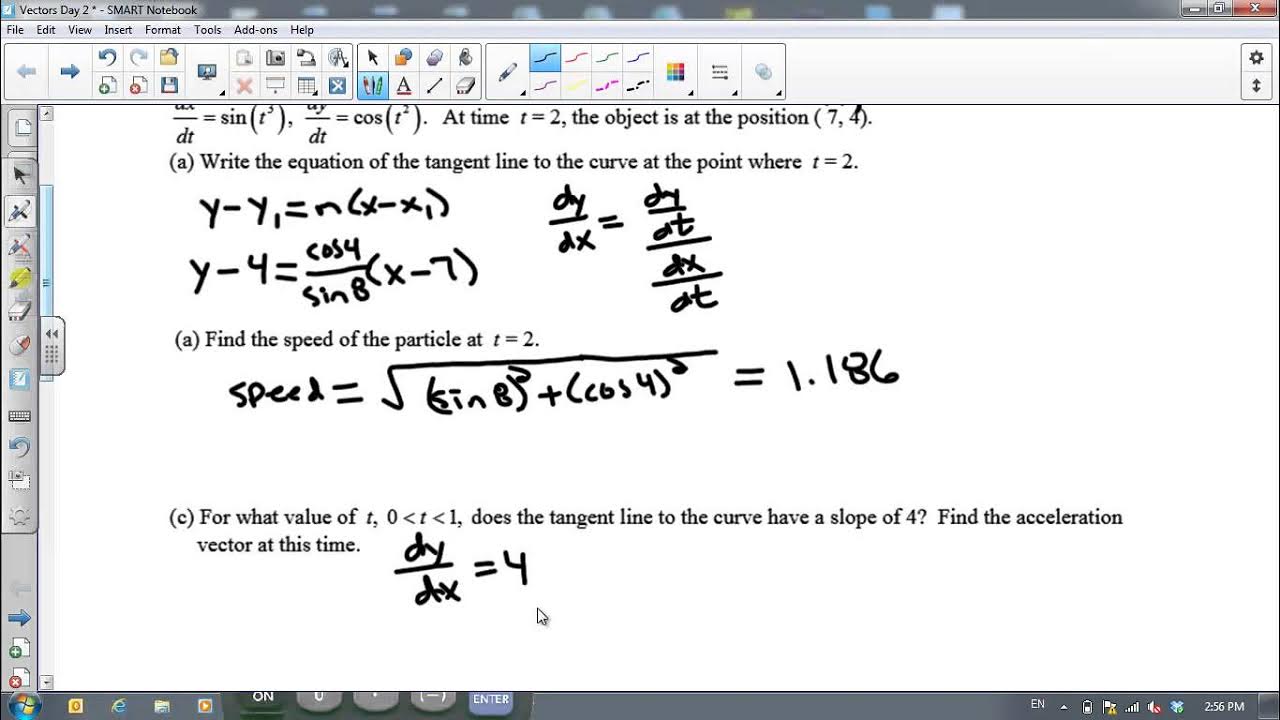
The problem-solving process is demonstrated with screenshots of calculations, ensuring clarity and accuracy.
The importance of starting the calculations at t = 4 is highlighted for consistency in solving the problem.
The transcript concludes with a wish for good luck, indicating a supportive and encouraging tone.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: