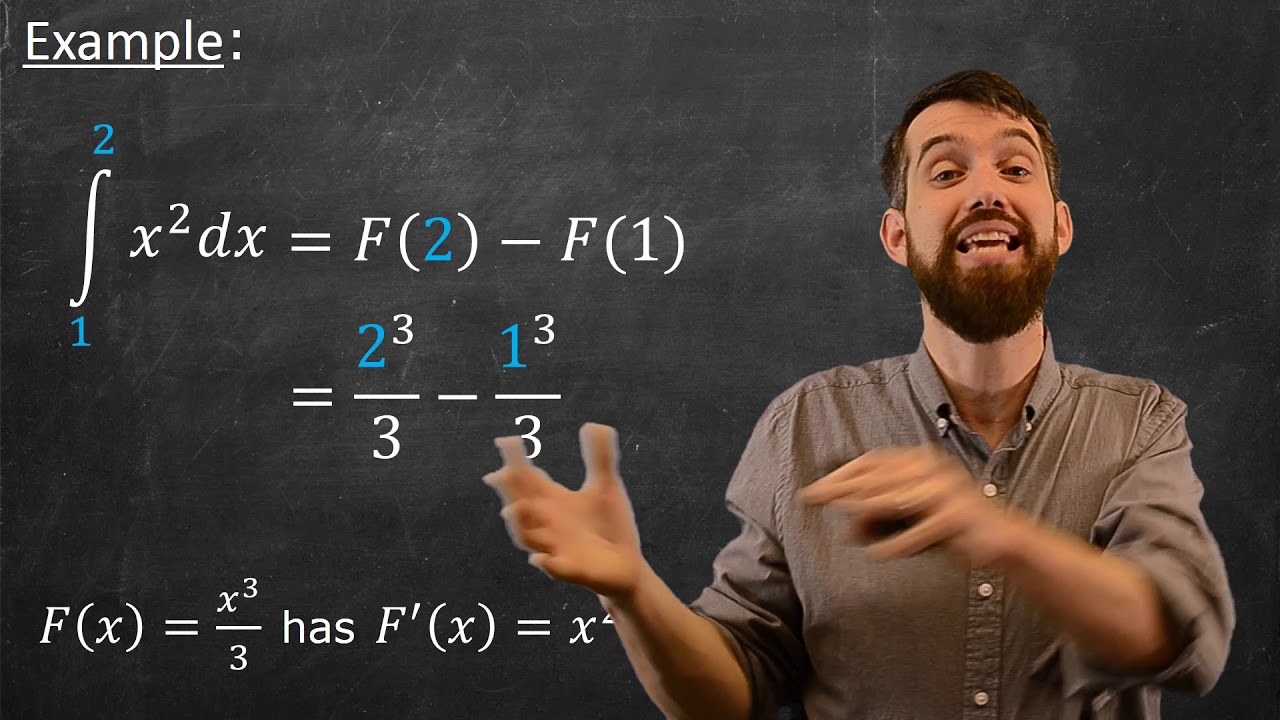Substitution Method for Definite Integrals **careful!**

Dr. Trefor Bazett
27 Oct 201704:51
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of substitution in indefinite and definite integrals. It explains that the antiderivative of a function F evaluated between two points A and B can be expressed as F(G(B)) - F(G(A)), where G is a function of X. The script then illustrates this concept with an example, integrating the square root of (1 + 3x) from 0 to 1. It guides the viewer through the process of identifying the substitution variable (u = 1 + 3x), finding the new limits (1 and 4), and the derivative (du = 3dx). The example concludes with the evaluation of the integral, resulting in a final answer of 14/3. The video emphasizes the importance of verifying the antiderivative by taking its derivative to ensure accuracy.

Takeaways
  • ๐Ÿ“š The substitution rule can be applied to both indefinite and definite integrals, allowing for the simplification of integration problems.
  • ๐Ÿ”„ When applying the substitution rule to definite integrals, the antiderivative is evaluated between the bounds of the integral, resulting in F(G(b)) - F(G(a)).
  • ๐Ÿ“ˆ The limits of integration also change with the substitution, from the original variable to the new variable's bounds, which are G(a) to G(b).
  • ๐Ÿงฎ The derivative of the substitution function (G'(x)) is crucial, as it affects the differential (du) in the new integral form.
  • ๐Ÿ“ An example given in the script involves integrating the square root of (1 + 3x) from 0 to 1, which requires identifying the substitution variable (u) and the bounds (G(a) and G(b)).
  • ๐Ÿ”‘ The substitution variable (u) is identified as the part of the integrand that will simplify the integration process.
  • ๐Ÿ” After identifying u, the bounds for the new integral are calculated by substituting the limits of the original integral into the u expression.
  • ๐Ÿงฌ The differential (du) is determined by the derivative of the substitution function, which in the example is the derivative of 1 + 3x, resulting in 3dx.
  • โœ… A quick check is suggested by taking the derivative of the proposed antiderivative to ensure it matches the original integrand.
  • ๐Ÿ“‰ The final step is to evaluate the new integral between the new bounds and apply the substitution back to the original variable to find the final answer.
  • ๐Ÿ”ข In the given example, the final answer is computed by evaluating the antiderivative of u^(1/2) between the new bounds and then converting back to the original variable.
  • ๐Ÿ“ The example concludes with the evaluation of the definite integral, resulting in a final answer of (14/3) after applying the limits of integration and the substitution.
Q & A

  • What is the substitution rule for indefinite integrals?

    -The substitution rule for indefinite integrals involves replacing a function with a new variable, which is often denoted as 'u', and then solving the integral in terms of this new variable. The result is expressed as some function of 'u' plus a constant of integration, C.

  • How does the substitution rule apply to definite integrals?

    -For definite integrals, the substitution rule allows us to change the variable of integration from 'x' to 'u', where 'u' is some function of 'x'. The limits of integration also change accordingly to reflect the new variable, and the integral is solved in terms of 'u' before substituting back the original limits.

  • What is the general form of the definite integral after applying the substitution rule?

    -The general form of the definite integral after applying the substitution rule is the integral from G(a) to G(b) of f(u) du, where G(x) is the function being substituted and f(u) is the integrand evaluated at u.

  • What is the example integral provided in the script?

    -The example integral provided is โˆซ from 0 to 1 of the square root of (1 + 3x) dx.

  • How is 'u' determined in the example integral?

    -In the example integral, 'u' is determined by setting it equal to the expression under the square root, which is 1 + 3x.

  • What are the limits of integration for 'u' in the example?

    -The limits of integration for 'u' are determined by substituting the original limits into the 'u' expression. So, u = 1 when x = 0, and u = 4 when x = 1.

  • What is the derivative of G(x) in the example?

    -The derivative of G(x) = 1 + 3x is dG/dx = 3.

  • How is the differential dx transformed in the example?

    -The differential dx is transformed into du by multiplying by the derivative of G, so it becomes 1/3 du, since the derivative of G(x) is 3.

  • What is the final integral expression after the substitution in the example?

    -The final integral expression is โˆซ from 1 to 4 of (1/3) * (u^(1/2)) du.

  • How is the integral of u^(1/2) solved?

    -The integral of u^(1/2) is solved by using the power rule for integration, which gives (2/3) * u^(3/2).

  • What is the final result of the example integral after evaluating the limits?

    -The final result is (1/3) * (2/3) * (4^(3/2) - 1^(3/2)), which simplifies to (2/9) * (8 - 1), resulting in 14/9 or approximately 1.56.

Outlines
00:00
๐Ÿ“š Understanding Definite Integrals with Substitution Rule

The paragraph introduces the concept of using the substitution rule for definite integrals. It explains that the antiderivative of a function F evaluated between two points A and B can be written in terms of a new variable u, which is a function of the original variable x. The limits of integration also change accordingly, from x=A to x=B to u=G(A) to u=G(B), where G is the function that transforms x into u. The paragraph concludes with a formula for the definite integral in terms of u.

Mindmap
Keywords
๐Ÿ’กSubstitution Rule
The substitution rule is a fundamental method in calculus for evaluating integrals by substituting one variable for another to simplify the integral. In the video, it is used to transform the integral of a function composed with another function into a more manageable form. This is illustrated when the script discusses the indefinite integral of the form f(G(x)) * G'(x) and its evaluation between two points A and B.
๐Ÿ’กIndefinite Integral
An indefinite integral represents the antiderivative of a function, which is a function whose derivative is the original function. The video script refers to the process of finding an antiderivative of a function without specifying the limits, resulting in an answer of the form 'function + C', where 'C' is the constant of integration.
๐Ÿ’กDefinite Integral
A definite integral is a specific type of integral that calculates the area under a curve between two points on the x-axis. It is defined as the antiderivative of a function evaluated at the upper limit of integration minus the antiderivative evaluated at the lower limit. The script demonstrates how to apply this concept to the integral from A to B of a function f(G(x)) * G'(x).
๐Ÿ’กVariable of Integration
The variable of integration is the variable that is being integrated with respect to. In the context of the video, the variable of integration starts as 'x' but is changed to 'u' when applying the substitution rule. This change is crucial as it allows the integral to be expressed in terms of 'u', simplifying the integration process.
๐Ÿ’กAntiderivative
An antiderivative is a function whose derivative is the original function being integrated. The video explains that the process of finding the antiderivative is central to evaluating both indefinite and definite integrals. The antiderivative is represented by the capital 'F' in the script, which is evaluated at the bounds of the integral.
๐Ÿ’กComposition of Functions
A composition of functions occurs when one function is applied to the result of another. In the script, the composition is represented by f(G(x)), where 'f' is a function and 'G(x)' is another function. The video uses the composition to illustrate how to apply the substitution rule to the integral.
๐Ÿ’กLimits of Integration
The limits of integration are the boundaries, often represented by 'a' and 'b', within which the definite integral is computed. The video script discusses how these limits change when the variable of integration changes from 'x' to 'u', specifically from 'G(a)' to 'G(b)'.
๐Ÿ’กDerivative
A derivative is a measure of how a function changes as its input changes. In the context of the video, the derivative of a function G(x), denoted as G'(x), is used to express the integral in terms of 'u'. The derivative is also used to verify the antiderivative found during the integration process.
๐Ÿ’กIntegration by Parts
Although not explicitly mentioned in the script, integration by parts is a technique that is closely related to the substitution rule. It is used when the integrand is a product of two functions, and it involves finding an antiderivative of the product by differentiating one function and integrating the other.
๐Ÿ’กPower Rule
The power rule is a basic rule in calculus that allows for the integration of polynomial functions. It states that the integral of x^n, where n is a constant, is x^(n+1)/(n+1) + C. The video script uses the power rule to find the antiderivative of u^(1/2), which is 2/3 * u^(3/2).
๐Ÿ’กConstant of Integration
The constant of integration, often denoted as 'C', is added to the antiderivative of a function to account for the family of functions that differ by a constant and still have the original function as their derivative. The script mentions this when discussing indefinite integrals and the general form of the antiderivative.
Highlights

The substitution rule for indefinite integrals can be applied to definite integrals as well.

The antiderivative of F evaluated between A and B is used, written as F(G(B)) - F(G(A)).

The definite integral can be rewritten in terms of a new variable u, with the limits of integration changing from G(A) to G(B).

The variable of integration changes from x to u, where u = G(x).

An example is given to illustrate the process, integrating from 0 to 1 of the square root of 1 + 3x dx.

The function u is identified as the part under the square root, 1 + 3x.

The bounds for u are determined by plugging in the limits of x, resulting in 1 and 4.

The derivative of the function G(x) = 1 + 3x is found to be 3, so du = 3 dx.

The integral is simplified by factoring out constants and combining terms to get 1/3 du sqrt(u).

The integral of sqrt(u) is solved, resulting in (2/3)u^(3/2).

The limits of integration are substituted back in, changing from 0 and 1 to 1 and 4.

The final answer is obtained by evaluating the antiderivative at the new limits and subtracting.

A quick check is done by taking the derivative of the antiderivative to verify the solution.

The final answer is 14/3, obtained by plugging in the limits and simplifying.

The substitution rule allows for a systematic approach to solving definite integrals.

The process involves identifying the function to substitute, finding the new bounds, and solving the resulting integral.

The technique can be applied to a wide range of integrals, demonstrating its versatility.

The example provided illustrates the step-by-step process in a clear and understandable manner.

The video concludes by emphasizing the importance of verifying solutions through differentiation.

Transcripts

Browse More Related Video

Average Value of a Function

AP Calculus AB Crash Course Day 8 - Integration and Riemann Sums

2023 AP Calculus BC FRQ #6

Adjusting the Constant in Integration by Substitution

Fundamental Theorem of Calculus II

Worked example: Derivative of รƒยƒร‚ยƒ(3x_-x) using the chain rule | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegralsSubstitutionDefinite IntegralIndefinite IntegralMathematicsExample WalkthroughRoot FindingEducational ContentMath TutorialDerivatives