Business Mathematics Calculus Midterm Review
TLDRThe transcript appears to be a detailed instructional dialogue, likely from a calculus lesson or tutoring session. The speaker covers a variety of mathematical topics, including limits, derivatives, and applications such as compounding interest and cost functions. They delve into the specifics of solving problems involving polynomials, factoring, and the application of the quadratic formula. The lesson also touches on the concept of indeterminate forms, particularly zero over zero, and how to handle them. There's a strong emphasis on the correct application of mathematical rules, such as the product and quotient rules for differentiation, and the use of the chain rule. The speaker provides step-by-step guidance on how to approach each problem methodically, highlighting the importance of clarity and accuracy in mathematical expression. The dialogue concludes with a discussion on the interpretation of the results in the context of business calculus, including total cost, marginal cost, and average cost analysis. The session is instructional and assumes a level of familiarity with calculus concepts.
Takeaways
- 📚 Start by understanding the basic rules of limits, such as any number over zero is infinity, negative infinity for a negative number, and zero over any number is zero.
- 🔢 When dealing with indeterminate forms like zero over zero, use algebraic manipulation to simplify the expression before evaluating the limit.
- 📈 In calculus, when finding the equation of a tangent line, you can use the point-slope form y = mx + b, where m is the slope (the derivative of the function at the given point) and b is the y-intercept.
- 🧮 To find the derivative of a function, apply the appropriate rules such as the power rule, product rule, quotient rule, and chain rule, depending on the function's form.
- 🛠️ For compound interest problems, use the formula A = Pe^(rt), where A is the amount of money accumulated after n years, including interest, P is the principal amount, r is the annual interest rate, and t is the time the money is invested for.
- 🔬 In related rates problems, you'll often need to find the derivative of an equation with respect to time, which can help determine how a quantity is changing over time.
- 📊 For optimization problems in business scenarios, calculate the marginal cost (the derivative of the total cost function) and the average cost to determine the optimal production level.
- 🤔 When evaluating limits, especially those involving infinity, remember that the limit of any function as x approaches infinity is simply the function's value at that point, which can be infinity.
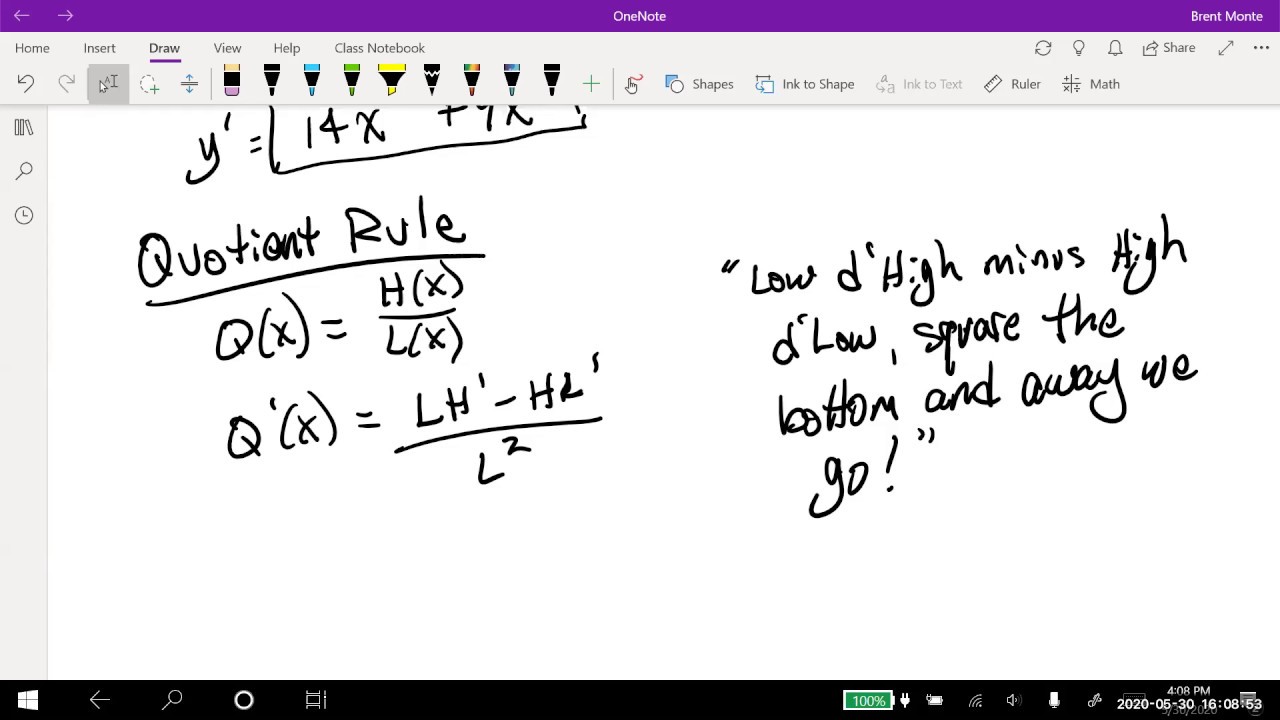
- 📐 Use the product rule for derivatives when you have a function that is a product of two other functions, and similarly, the quotient rule for functions that are quotients of two functions.
- 📝 When simplifying complex derivatives, it's important to present your answer clearly, as the method of representation can affect the understanding of the solution.
- 🔑 The concept of 'marginal' in business calculus refers to the derivative of a function, such as marginal cost or marginal revenue, which indicates the rate of change of the total cost or revenue with respect to the quantity produced.
Q & A
What is the first step when solving a limit problem involving a polynomial?
-The first step is to replace the variable, often denoted as 'n', with the value it approaches. If the result is a zero over zero form, you proceed with simplification or factoring.
How do you interpret a limit result of zero over zero?
-A limit result of zero over zero is considered indeterminate. It does not immediately equate to zero; instead, further simplification or algebraic manipulation is required.
What is the correct approach when you encounter an expression of the form one over zero in a limit?
-If you encounter one over zero, you stop and recognize that any number over zero is infinity, and negative any number over zero is negative infinity.
How do you simplify polynomial expressions?
-To simplify polynomials, you should factor as much as possible and then apply the appropriate algebraic rules, such as the difference of squares or combining like terms.
What is the process for rationalizing a denominator?
-Rationalizing a denominator involves multiplying by the conjugate of the denominator to eliminate radicals, simplifying the expression, and ensuring the final result has no radicals in the denominator.
How do you handle an indeterminate form like zero over zero during simplification?
-You can often resolve an indeterminate form like zero over zero by applying algebraic manipulations such as factoring, canceling out common factors, or using special product formulas.
What is the general formula for continuous compounding?
-The general formula for continuous compounding is A = Pe^(r*t), where A is the amount of money accumulated after n years, including interest, P is the principal amount, r is the annual interest rate, and t is the time the money is invested.
How do you find the equation of a tangent line at a given point on a curve?
-To find the equation of the tangent line, you first calculate the derivative of the function at the given point to find the slope (m). Then you use the point-slope form of a line, y - y1 = m(x - x1), where (x1, y1) is the given point on the curve.
What does the term 'marginal cost' represent in business calculus?
-In business calculus, 'marginal cost' represents the derivative of the total cost function, which indicates how the cost changes with an incremental change in the number of units produced.
How do you determine whether a function is increasing or decreasing at a particular point?
-To determine if a function is increasing or decreasing at a particular point, you calculate the derivative of the function at that point. If the derivative is positive, the function is increasing; if it's negative, the function is decreasing.
What is the significance of the quotient rule in calculus?
-The quotient rule is significant in calculus as it allows you to find the derivative of a function that is the quotient of two other functions. It is especially useful for functions involving fractions or ratios.
Outlines
🔢 Mathematical Operations and Limit Calculations
The paragraph discusses various mathematical operations, focusing on limit calculations. It covers the rules for handling different scenarios in limits, such as when dealing with zero over zero, infinity, and negative infinity. The explanation also touches on simplifying polynomials, factoring, and applying the quadratic formula. It emphasizes the importance of understanding the behavior of functions and their limits, as well as the correct application of mathematical rules and formulas.
📚 Simplifying Expressions and Rationalizing
This section delves into simplifying algebraic expressions and the concept of rationalizing. It explains how to handle expressions with radicals and how to simplify them by changing signs and multiplying by conjugates. The paragraph also covers the process of simplifying fractions and the importance of keeping terms with similar factors to cancel them out, resulting in a more straightforward expression.
📈 Calculus Applications: Tangent Lines and Derivatives
The paragraph explores applications of calculus, specifically finding the equation of a tangent line and calculating derivatives. It explains that a horizontal tangent line implies a derivative of zero and guides through the process of finding the derivative of a given function. The explanation also touches on the concept of continuous compounding and how to calculate the annual rate given an investment's growth over time.
💹 Financial Mathematics: Compounding and Investment Growth
This part of the script focuses on financial mathematics, particularly the concept of continuous compounding. It outlines the formula for continuous compounding and explains how to find the annual rate of return on an investment that triples in value over seven years. The explanation involves using the natural logarithm to solve for the rate and converting it to a percentage.
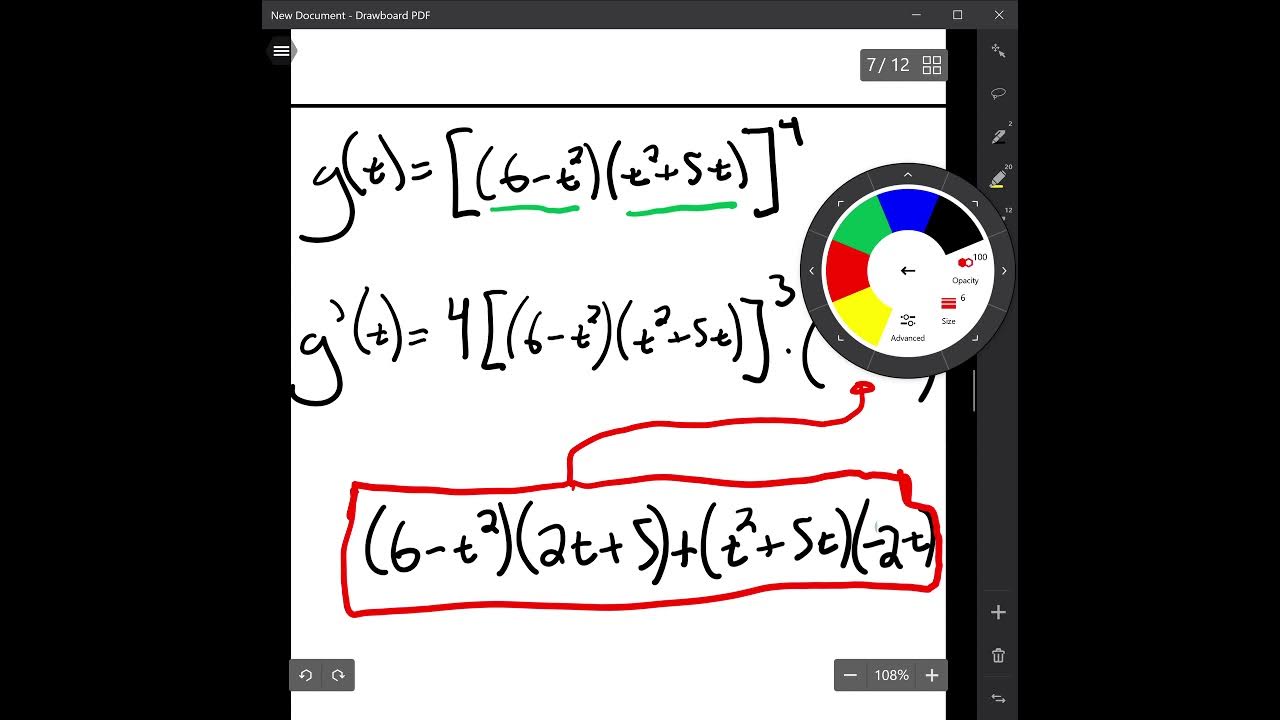
🧮 Derivatives and Their Calculations
The paragraph discusses the calculation of derivatives, emphasizing the importance of understanding the rules for differentiating various mathematical functions. It covers the quotient rule, product rule, and chain rule, providing examples of how to apply these rules in finding derivatives. The explanation also touches on the representation of answers and the efficiency of solving problems during exams.
📐 Derivatives in Geometry: Equation of a Tangent
This section focuses on the application of derivatives in geometry, specifically finding the equation of a tangent line to a curve at a given point. It explains the process of differentiating a given function to find the slope of the tangent line and then using the point-slope form to determine the equation of the tangent. The explanation also involves substituting given values to find the specific values of the slope and the y-intercept.
📉 Rates of Change and Related Rates
The paragraph explores the concept of rates of change and related rates in calculus. It discusses how to determine whether a quantity is increasing or decreasing by finding its derivative with respect to time. The explanation involves differentiating given functions and analyzing the sign of the derivative to understand the behavior of the function over time.
📊 Cost Analysis in Business Calculus
This section of the script deals with cost analysis in the context of business calculus. It explains the concepts of total cost, marginal cost, and average cost, and how to calculate them using derivatives. The explanation involves finding the derivative of the cost function to determine the marginal cost and then using it to analyze the cost behavior at different production levels. The paragraph also covers the interpretation of these costs in a business context.
🔑 Conclusion and Future Meeting
The final part of the script wraps up the discussion and outlines the next steps. It mentions that the test has been completed within the allotted time and confirms the next meeting on Thursday. The speaker ensures that all questions have been addressed and encourages students to continue practicing the concepts discussed.
Mindmap
Keywords
💡Derivative
💡Limit
💡Quotient Rule
💡Product Rule
💡Chain Rule
💡Continuous Compounding
💡Tangent Line
💡Related Rates
💡Marginal Cost
💡Average Cost
💡Exponential Functions
Highlights
The importance of understanding the behavior of limits, particularly when dealing with indeterminate forms like 0/0, and how to resolve them.
The concept of infinity in calculus and how to interpret different scenarios involving division by zero.
Techniques for simplifying polynomials by factoring and applying the quadratic formula where appropriate.
The process of rationalizing expressions involving square roots and the use of conjugates to eliminate radicals.
How to handle the application of derivatives in finding the equation of a tangent line to a curve at a given point.
The method for calculating compound interest continuously, using the formula for continuous compounding.
The application of derivatives to find the rate of change in various contexts, such as business and science.
The use of the quotient rule and product rule in deriving more complex functions, including those with radicals and exponentials.
How to apply the chain rule when differentiating composite functions, particularly those involving powers and roots.
The interpretation of the derivative in terms of marginal cost and how it can be used to analyze the cost function in business scenarios.
The calculation of total cost and marginal cost at a specific production level, and the implications for business decision-making.
The concept of average cost in production and how to calculate it using derivatives to find the average cost function.
The use of derivatives to determine the rate at which the average cost is changing at a particular production level.
The importance of clear and concise representation of mathematical solutions, especially when solving complex calculus problems.
Strategies for efficiently managing time during an exam, emphasizing the need to balance accuracy with speed.
The application of related rates in calculus to solve problems involving changing quantities over time, such as rates of growth or decay.
How to approach calculus problems systematically, breaking down complex expressions and applying the appropriate rules step by step.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: